-
Posts
699 -
Joined
-
Last visited
-
Days Won
3
Content Type
Profiles
Forums
Events
Posts posted by taeto
-
-
30 minutes ago, swansont said:
How is any of this relevant?
I hope in a similar way that some damning comments about the OP have so far not been considered irrelevant. He clearly has a record of mental illness, and he may honestly firmly believe that he has a scientific approach to the world somehow. He obviously has no leg to stand on in a science forum, and moderation has to intervene. Still a little bit of empathy instead of only cusswords is also in order.
0 -
As a possibly not entirely irrelevant side note, I got to thinking back at One Flew Over the Cuckoo's Nest, which for me installs the question in my mind, how would I deal with being put in a mental institution and how might my personality and powers of straight thinking have changed, if and when I got to leave it again to return to 'normal' society. Now the way that Jack Nicholson's character got entry into the system isn't likely the way that I would manage to do it. But you can think of scientists who in earlier times got close, such as Alan Turing, and others certainly did, like Cantor and Boltzmann. Alan got put on medication to remove his immoral homosexual deviance, which apparently eventually lead to suicide. Had that not happened, maybe he could have been due for more institutionalized 'treatment'.
I am likely about ten times more intolerant of nonsense than Strange, especially of the mathematical kind. Though mainly with the malicious type; usually cranks who declare that anything done by Cantor or Einstein must have been wrong, because they advanced into new directions less intuitive, and sometimes the objections are of a racist nature. That is different with Adom, who actually explains what he is observing, and how he calculates measurable quantities from his observations. He runs his conclusions out along strange tangents, granted. But there is nothing that I have seen of the usual malicious nature.
Adom explains his background in his book A Devastating Journey: Nova Scotia's Mental Health System. I haven't read it. It is likely that some of it is very factual. Maybe it goes to explain some of the directions that he is taking, with doing strange computations and distributing them via a forum such as this.
0 -
27 minutes ago, joigus said:
What part of this couple of sentences you didn't understand, taeto? I wasn't talking to you when I said it, but anyway, as you seem to care so much...
And sorry for 'patronizing' you. Really.
You are right, I apologize for being so bitchy.
I care a little bit, because I wanted to find a good argument for the integral, and I could not readily do that. Your 'pedestrian way' ought to provide the correct answer. But it does not work as a formal proof, unless you can show that the integrals converge as Lebesgue integrals. Something like the Henstock-Kurzweil integral may work even if Lebesgue does not.
0 -
3 minutes ago, joigus said:
There are more integrals in this world. Have you ever heard of the Lebesgue measure? I often think of integrals in terms of the Lebesgue measure. The trick is looking at the domain and the range of the function. "The range is infinite" becomes no more worrying than "the domain is infinite." Another name for it is mathematical power. No matter how you want to do it with Riemann, you're gonna have to face the singularities, because those are in the domain. If I've found them with my method, believe me, you're gonna find them too. No integral handbook in the world will get around that. That's a property of the integral, not of my method. I may take a look at how rigorously it is defined with the Lebesgue measure. Maybe Cauchy's theorem. But not now.
Most integrals in QFT are Lebesgue or Cauchy complex, not Riemann. Think just a little bit outside the Riemann box, please.
I said "this reduces to" about the simple algebraic steps, not the convergence arguments.
I honestly think I should go to sleep now, but who knows. I'm finding it difficult lately.
Please do not patronize.
The theorem that I mentioned specifically concerns the Lebesgue integral. Before that I already mentioned that we cannot be talking about the Riemann integral, because that is not even defined for this integrand with the given integration domain.
Now you should justify your "this reduces to". Typically by appealing to the monotone convergence theorem or to the dominated convergence theorem for Lebesgue integrals. Or to something else?
0 -
Thanks joigus for following up on this!
It is a mistake when you say "this reduces to". Because it will not be difficult to come up with examples like \[ \int_a^b f(x)+g(x) dx\] where \(f\) and \(g\) are both not defined in the entire interval \([a,b]\) and where \[\int_a^b f(x)+g(x) dx \neq \int_a^b f(x)dx + \int_a^b g(x)dx\] holds, even when all those three integrals converge.
The Riemann integral is not defined unless the integrand is defined throughout the integration interval, and this is not the case here. In such a case when it is not defined, you can resort to the theorem that if the number of discontinuities is countable you can ignore them. But that only goes when the integrand is bounded in absolute value, which in our case it is not.
So however much I want to believe your solution, I think we should offer yet a better proof.
0 -
Zodiac has gone full circle.
1 -
6 minutes ago, Zodiac said:
Within an already created , established system , maybe so .
Then the system that you are talking about, in which an electron spontaneously disintegrates, might be neither created nor established. And that is the only reason why we never see it happen, an electron going off like a firecracker?
0 -
12 minutes ago, Zodiac said:
no mechanical bond of the electron to retain stability !
I think the point the physicists are making is that the electron on its own is not unstable. it does not decay.
0 -
1 hour ago, Zodiac said:
I will return later to discuss the strong force required to stop virtual particles self annihilation ! (Atomic model)
Will that be in this thread or in a new thread?
In a thread which explicitly discusses gravity, it should be quite interesting and novel to combine it with a discussion of the strong force.
Let me guess: at a certain distance between nucleons, they are attracted to each other because of the existence of vacuum in between them. But as they approach each other too closely, they get repulsed, because they physically bump into each other in a similar fashion as billiard balls?
0 -
36 minutes ago, Mordred said:
Lol good luck tracking every math theory on compactification.... You can nearly get PH.D on the topic
Maybe nowadays. In my time it was just a trick that we learned in a first course on topology. Actually the textbook for the course was probably on mathematical analysis. I would not have expected that this topic would come to any notoriety in the mean time. If a student would come to me and suggest to write a PhD on compactification I would try to dissuade, since it does not seem a serious research topic. Maybe I am just too out of touch.
0 -
14 minutes ago, Displayer102 said:
Don't you add them together and set it equal to zero. Then make it a matrix and row reduce them. then after all that its left with have c_1=0, c_2=0 and 0+0
You are doing too much work.
To show that \(x^2-2\) and \(x-2\) are linearly independent polynomials, you have to show that the equation \(c_1 (x^2-2) + c_2 (x-2) = 0,\) as a polynomial equation, has \(c_1=c_2=0\) as the only solution. This is very easy, because \(c_1 (x^2-2) + c_2 (x-2) = c_1x^2 + c_2 x - 2(c_1 + c_2) = 0x^2+ 0x+0\) immediately tells you that \(c_1=0\) and \(c_2=0,\) just from looking at the coefficients of the powers of \(x\).
All that is left is to argue why \(W^\perp\) does not have additional polynomials in its basis other than these two.
0 -
2 hours ago, Displayer102 said:
a)p(x)=ax2+bx+c∈W⊥ if and only if 2a+2b+c=0
b) Basis is [2,2,0]
The elements of the basis are polynomials. You correctly found that the polynomials in \(W^\perp\) have the form \(ax^2+bx+c,\) where \(2a+2b+c=0.\)
The basis of \(W^\perp\) has to be a set of two polynomials which satisfy this. You could choose \(\{x^2-2,x-2\}.\) You said this already. Do you know how to prove that the set of these two polynomials make a basis for \(W^\perp\)?
0 -
It looks like you are doing more work than you need to. And some mistakes.
Towards the end of your long calculation of \(\langle p, x+1\rangle\) you assume \(p(0)=0?\) But if \(p(x)=ax^2+bx+c,\) then you have \(p(0)=c.\) I guess you just forgot to type it in.
So your conclusion that \(p(x)=ax^2+bx+c \in W^\perp\) if and only if \(2a+2b+c=0\) is correct.
And you correctly found two linearly independent solutions to this equation.
Your solution is correct.
0 -
You can answer question (a) easily, I assume?
And for any \(q(x) \in P_2\) you know the condition for determining whether \(q(x)\) is in \(W^{\perp}\)?
0 -
1 hour ago, MigL said:
The difference is the Mathematical version has to necessarily be more generalized, to encompass more cases, while the Physical version is more specific, and usually pertains to the case of 'limiting dimensions' by examining boundary conditions.
That sounds fair to me. At least I hope you are right. In which case a mathematician will accept some transformations to be eligible for the status of being compactifications that a physicist would not, and maybe that would be the only difference. I hope that there are no transformations that physicists will deem to be compactifications but mathematicians would not agree to. That would make communication difficult.
I get the sentiment that physicist mentality says "do not come here to our two horse town with your law from the big city; we have six-gun justice here, and this town may be too small for the both of us (sound of click)." Once you hear it, you try to adjust. Just kidding.
0 -
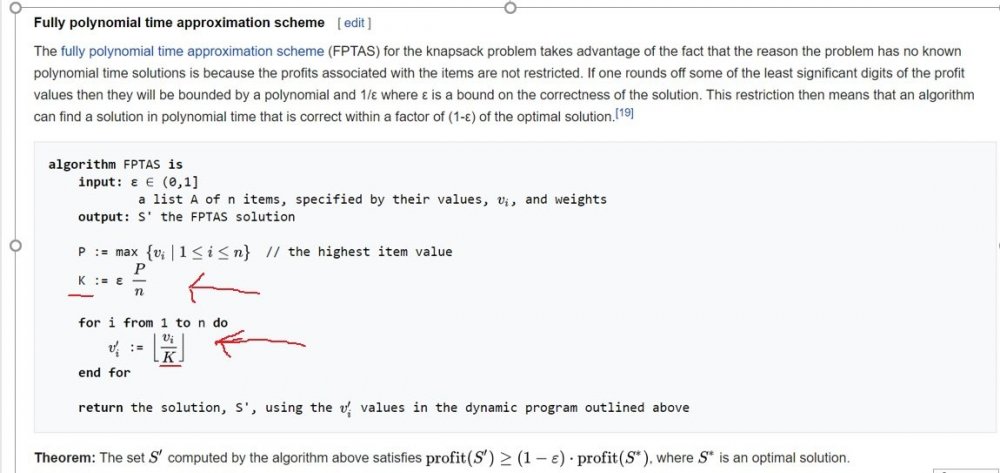
11 hours ago, zak100 said:
Hi,
I am trying to understand the FPTAS for the knapsack problem. I have got the following from wikepedia:
I have following questions:
(a)It shows two 2 ‘k’ symbols. I can’t understand the difference between them.
(b)Why its dividing the value v_i with the value of ‘K’ which is a ratio of P/n multiply by epsilon
(c)what is the significance of Epsilon?
(d)why rounding would convert the problem into a polynomial time problem?
Hi again Zulfi!
(a) It is the same K, only the author used different typesetting, first for a K in normal text font, second with a K in math font.
(b) It makes the new value \(v_i'\) into a whole number value that is large (if \(\varepsilon\) is small) compared to the original real-valued \(v_i\).
(c) If \(\varepsilon\) is small, then the new \(v_i'\) is big, and its size tells you about the size of \(v_i\) relative to the average \(P/n\) of all the different sizes.
(d) On https://en.wikipedia.org/wiki/Knapsack_problem you also have the dynamic programming algorithms that solve the problem in polynomial time for the new rounded weights.
0 -
20 hours ago, studiot said:
If we wish to base the discussion on set theory a good place to start is Menger's axioms
D1 : The empty set has dimension -1
D2 : The dimension of a space is the least integer, n , for which every point has arbitrarily small neighbourhoods whose boundaries have dimension less than n.
Suspecting this may not be relevant to the thread. But out of curiosity: what are the simplest meanings of 'small neighbourhood' and 'boundary' that you can come up with, which are based on set theory?
0 -
16 hours ago, studiot said:
You entirely missed the point of my comment.
Is the dimension of R2 two or is it one since every point in the plane can be referenced from a suitably winding line.
Possibly.
Viewed as having only the structure of a set you could in principle coordinatize \(\mathbb{R}^2\) using a bijection to \(\mathbb{R}.\) Despite that, I suspect at least two separate reasons for not declaring the 'set-wise' dimension equal to one.
For one thing we have the superior concept of cardinality to make a much finer distinction between sizes of sets.
And second, we prefer to restrict the concept of dimension initially to vector spaces, and then extending it also to manifolds. These structures allow coordinatizations that are faithful to their respective topologies, in the sense that any two points that are sufficiently close together in the space have representations that are also close together. That would not be the case for your coordinatization of \(\mathbb{R}^2,\) as the coordinates of the points in an open set would be scattered all over the real line.
Actually the concept of dimension gets applied to a structure like a finite graph in a different way than by looking at its graph theoretic properties. Instead its dimension gets defined by associating a vector space with the graph and then identifying the dimension of the vector space with the dimension of the graph itself.
16 hours ago, studiot said:and what about relatively compact and normed spaces?
From which point of view? They describe special cases of compact sets and vector spaces, respectively.
0 -
3 hours ago, Mordred said:
The description there is indeed similar to the standard definition of a topological space. It does contain the unfortunate phrase 'arbitrary number', when it should have read 'arbitrary collection'. Sometimes 'number' is understood to be a natural number, and that is certainly not the intention.
2 hours ago, studiot said:"A configuration is said to be n-dimensional if the least number of real parameters needed to describe its points is n."
It is true that we say that. But I suspect it is because we know from linear algebra, or similar, that this number n is an invariant of the configuration. For the example of a well-known space such as \(\mathbb{R}^2\) we are used to familiar coordinates \(x\) and \(y\) to communicate the position of points. But we are still free to choose a \(y\)-axis at 45 degrees angle to the \(x\)-axis and transform it by \(y \to -y^3\) if we prefer. It does not change the basic properties of the structure in any way. It still has points with two coordinates \((x,y),\) only they are in different places than what we are used to seeing.
So even for such a familiar 2-dimensional object it is not like we can freely speak of some particular dimension, unless we know how the structure is coordinatized.
0 -
Since the few stabs taken so far concern either electrostatics or mechanical stability, this could be moved to either a physics section, or to the puzzles.
0 -
32 minutes ago, Mordred said:
The above could be considered incorrect.
A topological space can a set of points with a line through it. However this example has no distance function.
A metric space must have a distance function. A metric spaces are topological spaces but not all topological spaces are metric spaces.
The term spacetime itself is erroneous one can topological spaces in Euclidean etc where there is no need for a time dimension or another example being a two dimensional phase space.
Indeed. The entry seems to want to describe 'compactification of a dimension'. This expression implicitly says that dimensions, coordinates, and a metric are all present. I will revise accordingly.
A topological space is not 'a set of points'. It is a pair of sets, one of which is a set of 'points', the other is a set of 'open subsets' of the set of points. Compactness is not a property of the set of points. E.g. the interval \([0,1]\) is compact in the usual Euclidean topology induced by Euclidean metric. It is non-compact in the discrete topology, in which every subset is open, because you can cover it by singleton sets, in which case you need to have continuum many of them. You can compactify this particular space by adding one new element \(\infty\) and one new open subset \([0,1]\cup \{\infty\}.\)
Yes, a metric space has a natural topology induced by the metric, in which the 'open balls around points' determine a basis for the topology. If we talk about a metric space, then we can naturally talk about topological properties such as 'compactness', 'connectedness' etc. in terms of that topology. We remain aware that other topologies on the same set are possible, such as the discrete topology and the trivial topology (in which the whole set and the empty set are the only open sets), and those topologies exhibit different properties.
Spacetime spilled over from the original entry. I am not sure exactly how to deal with it. But it seems the primary example of the use of 'compactification of a dimension' to appear in physics. A phase space is another example, so I should include it.
Hence:
In physics, compactification of a dimension means changing a model of [[spacetime]] or a [[phase space]] with respect to one of its coordinates. Instead of having this coordinate being infinite, one changes the model so that the coordinate has a [[compact space|compact]] range of finite length, and it may also be [[Periodic function|periodic]].
0 -
45 minutes ago, joigus said:
Gaussian elimination does not help here.
It is perhaps not so clear.
We have a product \(AB\) of matrices, where \(A\) has more rows than columns.
Suppose that if we perform an elementary row operation on \(A\) to produce a new matrix \(A',\) then there is a matrix \(B'\) for which \(AB=A'B'.\) (This is supposed to be the only tricky part.)
Then since by elementary row operations we can bring \(A\) into a matrix \(\bar{A}\) that has at least one all-zero row, there will be a matrix \(\bar{B}\) for which \(AB = \bar{A}\bar{B},\) such that the latter matrix has at least one all-zero row.
Now it follows from the formula for the determinant that \(\bar{A}\bar{B},\) and therefore \(AB,\) has determinant zero.
1 -
Suggestion: I will edit the beginning of the wikipedia entry on compactification_(physics) which now reads
In physics, compactification means changing a theory with respect to one of its space-time dimensions. Instead of having a theory with this dimension being infinite, one changes the theory so that this dimension has a finite length, and may also be periodic.
into
In physics, compactification means changing a model of [[spacetime]] with respect to one of its coordinates. Instead of having this coordinate being infinite, one changes the model so that the coordinate has a [[compact space|compact]] range of finite length, and it may also be [[Periodic function|periodic]].
Motivation:
The entry in wikipedia for 'dimension' says that this is the number of coordinates used to describe a space. It doesn't seem correct to say that the dimension of spacetime is infinite. It is a coordinate (function) that can be infinite.
Changing a coordinate representation of spacetime does not 'change a theory', it changes a model.
Requiring the compactified coordinate be compact is the issue I want to ask the experts about. I think that I get from Mordred's contributions that this is a correct interpretation. And if so, then I would like the wikipedia entry to express it. The existing phrase implicitly indicates that it does not have to be compact. But how can I be certain that it isn't correct, and there are instances of 'compactification' in physics which modify a coordinate into a 'small' but non-compact function? It appears that Kaluza-Klein and Yang-Mills do insist on a compact outcome.
Other improvements will be much appreciated.
0 -
Can you use Gaussian elimination?
0



The Ethics of Strange
in Suggestions, Comments and Support
Posted · Edited by taeto
I documented that he authored a book that describes his experiences with being transferred from his home near Windsor, ON, to become a subject of Nova Scotia's mental health system. So maybe you are right to say that I "infer" something about his mental health. To say that I "offer diagnosis" is a little far fetched. A diagnosis can assume to have been established already before the act of confining a person to a psychiatric institution. Would you be happy if I suggested that you seem to offer the opposite diagnosis, probably not.
Yes, the moderation is excellent in this case, as always. I came to this thread by clicking on the Topics menu on the upper right side of the home page, and there it does not tell you which forum it takes you to. From the title of the thread I just assumed it would be the Ethics subforum, rather than the moderation forum, or I would have made a different post. I only have problems with some of the comments that appear to be directed at the OP. Who I imagine to be not of the best of health and likely mentally fragile and in need of support. It seems to be just me making that error. So I have to apologize for that.