DanielMB

For 25 seconds of arc (app. 0.41º) the separability should be expressed as S(x) = 0.0292 x

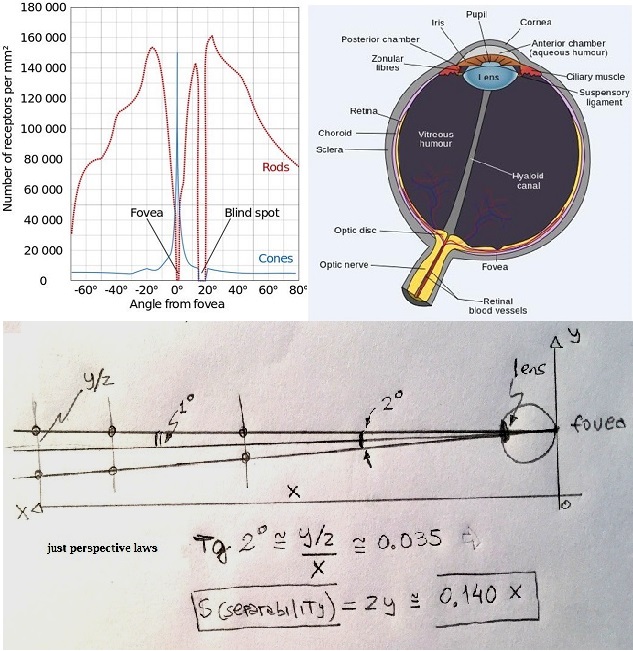
NobleKnight, Hi, Rods are photoreceptor cells sensitive to low luminance levels (scotopic vision and mesopic -transition zone-) Cones are photoreceptor cells sensitive to medium and high luminance levels (photopic vision and mesopic) Rods and Cones consitute the first layer of photoreceptors in the retina that interact with light entered the eye Cones are concentrated mainly in the fovea region (0°-10°) (look at the first attached image, where you can see the rods and cones distribution) Rods are concentrated almost exclusively in the extra-fovea peripheral region (>10°) There are three types of cones in the HVS, denoted S, M, L, each group is characterized by a proper responsivity curve to light wavelength, Short, Medium and Long wavelength respectively SML are frequently related to specific color stimulus, but not in rigorously way S is related to a Blue stimulus, M to a Green, and L to Red The population distribution of Cones is approximately S:M:L = 12:6:1 Cones are responsible for our trichromatic vision in the photopic and mesopic regions 2º in the fovea region means to take as first aproximation the fovea as point from a distant object covering those 2º, look at the third image, this picture consideres the fovea as a point and the object following perspective laws, the law you are asking for is just: S = 0.140 x being x the distance from the object to the fovea and S the object "size" (height) You have to take care with the scope of the perspective laws I've written, just because there are other phenomena appearing when distances are not short distances (i.e. 10 mts or less), visibility has impact on our HSV (human system vision) affecting our criteria, using a substractive filter model, you can take it into account through the Beer-Lambert law, where image intensity decreases in an exponential way with distance, but this is other question ...

@Studiot Thanks for your answer. Maupertuis deduced Snell's laws (reflexion and refraction laws), you can see it in this link : https://fr.wikisource.org/wiki/Accord_de_différentes_loix_de_la_nature_qui_avoient_jusqu’ici_paru_incompatibles Search for the paragraph #424, explicitly Refraction Law but minimizing and incorrect funcion : v.dl, so he arrives to the law , but using as refraction index n = v/c (incorrect) and not n = c/v (correct), just because his respect to Descartes and Newton (v>c in optical densed media -obviously incorrect-), so we had to wait until XIX century for the Fizeau experiments to elucidate that the corpuscular theory of Newton & Descartes was wrong, and light moves slowly in a densed media, but not Fermat nor Maupertuis, even Euler knowed that ... Yes, you are right when you express that the "minimization" could be in a certain specific scenarios valid as "maximization", and others where the "critical point" is a saddle point, as it is showed in this Gray's paper: http://www.eftaylor.com/pub/Gray&TaylorAJP.pdf So, being rigorous, LAP (Least Action Principle) should be abreviated as CAP (Critical Action Principle) It's rather difficult to read Maupertuis in the web, because most of the letters to the french Academy are in french, Euler sent his letters to Maupertuis in latin and Maupertuis answered then also in french ....

@Studiot I know Maupertuis' action is different from the modern concept of action, in fact when the total energy E is conserved, the Hamilton-Jacobi equation can be solved, emerging Maupertuis' abreviated action What I've questioned is the first Maupertuis definition of action as the sum of <<<< v.dl >>>>>>, this definition does not minimize the time insumed by light in the trajectory, the correct abreviated action for the light should have been defined as <<< (1/v).dl >>>> , this definition does minimize the time insumed by light in the trajectory!!!!! And the cause of Maupertuis' error was to believe (following Descartes) that light moves quickly in a dense media than it does in vacuum Notes : Hero of Alexandria arrived to similar conclusions as Fermat did, but Hero only analyzed propagation and reflexion, not refraction, while Fermat included refraction, Maupertuis created and added epistemological significance to the term "action" an with Euler extended the scope of the principle

No, the question was not answered yet, but yesterday while I was reading Maupertuis Memories and many letters between him and Euler about the theme, I have arrived to the correct answer. I’ll use the following reference … 1) Accord de différentes loix de la nature qui avoient jusqu’ici paru incompatibles https://fr.wikisource.org/wiki/Accord_de_différentes_loix_de_la_nature_qui_avoient_jusqu’ici_paru_incompatibles In Reference #1, Maupertuis says (in the paragraph @423) … "elle prend une route qui a un avantage plus réel: le chemin qu’elle tient est celui par lequel la quantité d’action est la moindre." "Il faut maintenant expliquer ce que j’entends par la quantité d’action. Lorsqu’un corps est porté d’un point à un autre, il faut pour cela une certaine action, cette action dépend de la vîtesse qu’a le corps & de l’espace qu’il parcourt, mais elle n’est ni la vîtesse ni l’espace pris séparément. La quantité d’action est d’autant plus grande que la vîtesse du corps est plus grande, & que le chemin qu’il parcourt est plus long, elle est proportionnelle à la somme des espaces multipliez chacun par la vîtesse avec laquelle le corps les parcourt." … "(The light) takes a trajectory that has a real advantage : the followed trajectory is that with the least amount of action." "It is mandatory to explain what I understand by action quantity. When an object is carried from one point to other, does exist a certain action, this action depends on the velocity of the object and the length of the followed trajectory, but it is not the velocity nor the length taken separately. The action amount is bigger as the object velocity is also bigger, and when the trajectory increases its length, IT’S PROPORTIONAL TO THE SUM OF THE LENGTHS MULTIPLIED BY THE VELOCITY OF THE OBJECT" The text I highlighted in uppercase means (or could be interpreted as) the integral of v.dl That’s wrong!! For the light, the integral that minimizes the time is (1/v).dl and not v.dl The reason is the following : In Reference #1, Maupertuis says (in the paragraph @422) “Descartes avoit avancé le premier, que la lumière se meut le plus vîte dans les milieux les plus denses” “Descartes had advanced at first that LIGHT MOVES MORE QUICKLY IN MORE DENSED MEDIA” Maupertuis followed Descartes & Newton in his maths, so commited the error of evaluating the optical path with that incorrect hypothesis, because LIGHT MOVES MORE SLOWLY IN MORE DENSED MEDIA. That's the reason because I could not understand Maupertuis PLA in his enunciation Thanks

Could anybody tell me how Maupertuis based on his definition of action (S) supposedly arrived to similar results as Fermat did it with (S*)?

Yes, that was the idea ... thanks

Fermat found that light in its propagation, reflection and refraction follows the trajectory with the least time, that could be expresed as a proto-action S* (not defined by Fermat) S* := Integral[(1/v).dl] S* = (1/c).Integral[(c/v).dl = (1/c).Integral[n.dl] = (1/c).Lo Where Lo is the optical path, so minimizing S* is equivalent to minimize Lo, besides … S* = Integral[(1/v).(dl/dt).dt] = Integral[dt] So minimizing S* is equivalent to minimize the time used in the trajectory. On the other hand, originally, Maupertuis indentified the action for light as S = Integral[v.dl] How it can be reconciled?, being S* # S, is this an error in Maupertuis notes? Please, be benevolent, I’m not a physicist. Thanks a lot

Yes, there are, as an example we can see that male Bower birds seduce females decorating nests as you can see in the picture, Sorry, I haven't seen it before sending my post ....