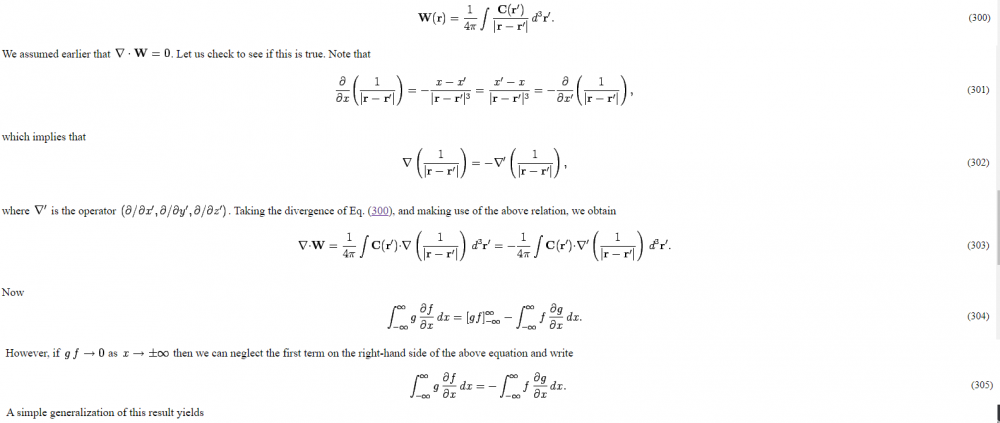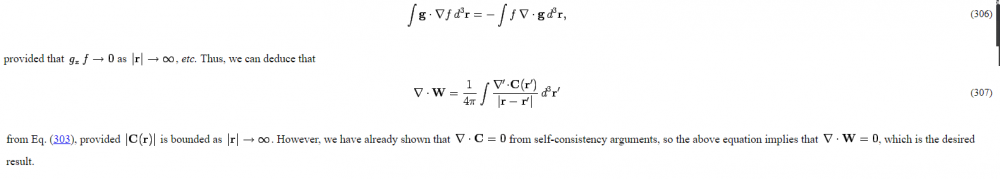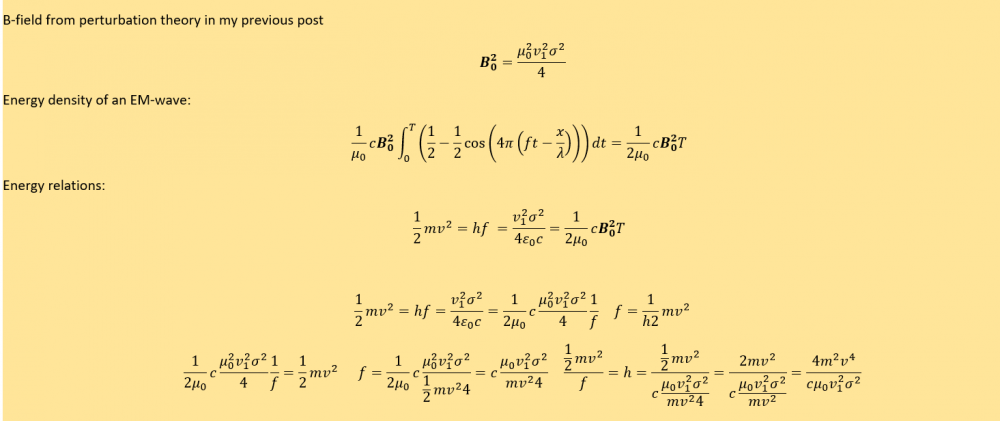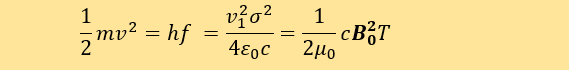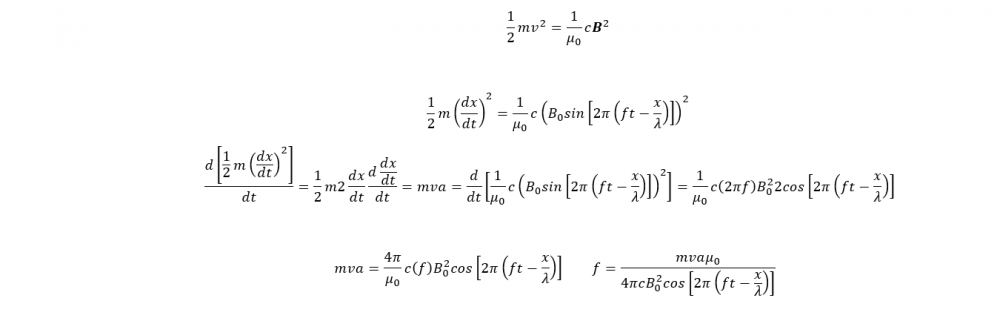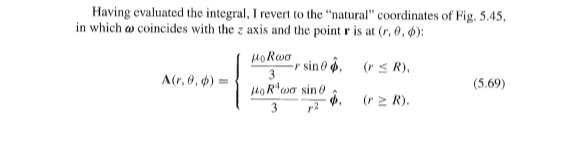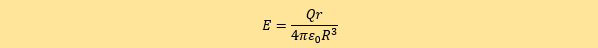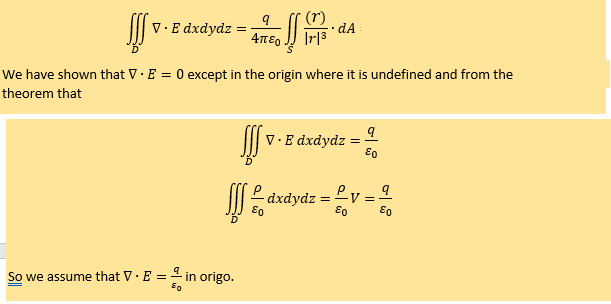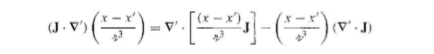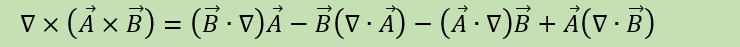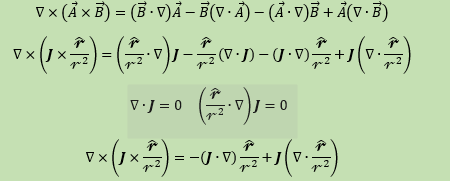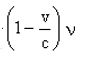-
Posts
42 -
Joined
-
Last visited
Content Type
Profiles
Forums
Events
Everything posted by Tor Fredrik
-

problem in proof for magnetic vec pot is 0
Tor Fredrik replied to Tor Fredrik's topic in Classical Physics
-

problem in proof for magnetic vec pot is 0
Tor Fredrik replied to Tor Fredrik's topic in Classical Physics
What other components could there be? -
I have tried to go through a proof for this which is used in physic texts: $$\nabla \cdot \vec{A}=\frac{\mu _0}{4\pi}\nabla \cdot \int \frac{ J(r')}{|r-r'|} dV'$$ again we use $$ \nabla \cdot \frac{ 1}{|r-r'|}=-\nabla' \cdot \frac{ 1}{|r-r'|}$$ If you go through the equations you would obtain that you could write: $$\nabla \cdot \vec{A}=-\frac{\mu _0}{4\pi} \int J(r') \cdot \nabla' \frac{ 1}{|r-r'|} dV'$$ Then they look at the integration as from integration by parts $$\int_{-\infty}^\infty g \frac{\partial f}{\partial x} dx = [gf]_{-\infty}^\infty - \int_{-\infty}^\infty f \frac{\partial g}{\partial x} dx$$ initially the integral is over the current which does not go from $$-\infty \:\: to \:\: \infty$$. I could perhaps reason and say that integrating from $$-\infty \: to \: \infty$$ would get the same result. But if we extend the reasoning I did get to For the $$-\infty \:\: to \:\: \infty$$ we did get: $$\nabla \cdot \vec{A}=-\frac{\mu _0}{4\pi} \int_{-\infty}^\infty J(r') \cdot \nabla' \frac{1 }{|r-r'|} dV'$$ $$ J(r') \cdot \nabla' \frac{1 }{|r-r'|}=J(r') \cdot[\frac{\partial}{\partial x'}\textbf{i}+\frac{\partial}{\partial y'}\textbf{j}+\frac{\partial}{\partial z'}\textbf{k}] \frac{1}{[(x-x')^2+(y-y')^2+(z-z')^2]^{0.5}}$$ for the first component: $$ g=J_x(r')$$ $$f=\frac{1}{[(x-x')^2+(y-y')^2+(z-z')^2]^{0.5}}$$ If we would have kept the integration limits from dV' it would be apparent that $$ [gf] \neq0$$ If we increase to from $$-\infty \:\: to \: \: \infty$$ it would be apparent that $$\int_{-\infty}^\infty g \frac{\partial f}{\partial x} dx $$ would not change after the increase in integration limits to $$-\infty \: \: to \: \: \infty$$ and $$- \int_{-\infty}^\infty f \frac{\partial g}{\partial x} dx$$ would change since $$\frac{\partial g}{\partial x} $$ is undefied when the current density ends but with from $$-\infty \:\: to \:\: \infty$$ we would get $$ [gf]_{-\infty}^\infty =0$$ which is a change? How does this prove that $$\nabla \cdot A=0$$ ? Additional info: Here is a proof from a physic text just in case. C below is used as current density above:
-

attempting to isolate frequency of an EM-wave
Tor Fredrik replied to Tor Fredrik's topic in Classical Physics
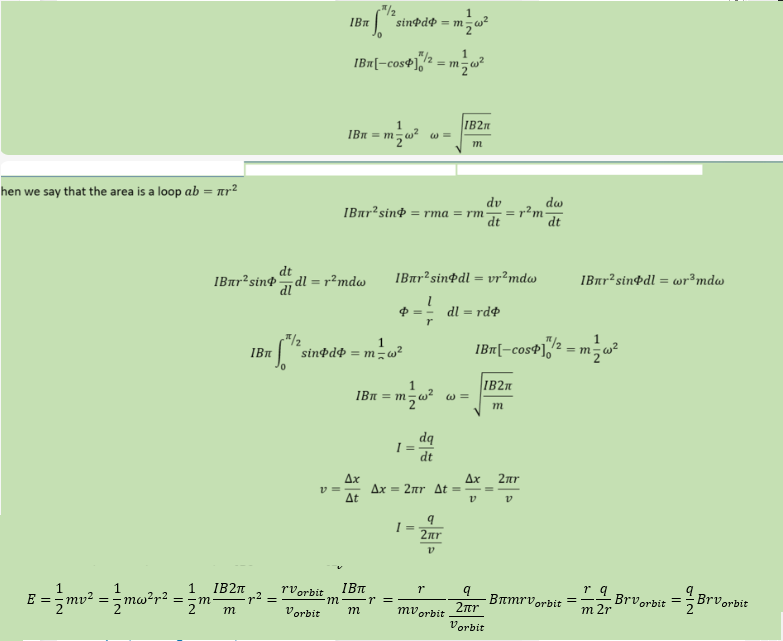
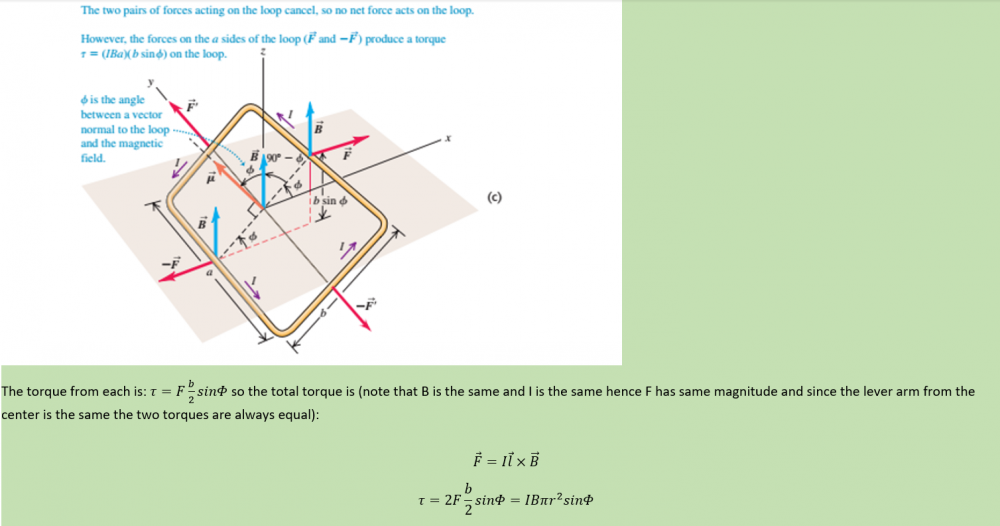
When the coil has turned 90 degrees it reaches equilibrium and deaccelerates to 0 velocity. Lets assume hypotetically that all this energy is released as one photon. Now I will try to introduce radiation pressure: So we hypotetically want the electron that has been deaccelerated to 0 velocity (I will ignore the current direction) to obtain the same kinetic energy and velocity. We want it to absorb a photon to do so. If we look at one half cycle of an EM wave that would be half of the energy of one photon if all of the energy of the photon is contained in one cycle. The EM wave exert radiation pressure as described above. It is also said that E=pc where p is radiation pressure density and E is energy density. Over a half cycle of an EM wave the avearge cycle can be obtained the following way: In order to calculate the amplitude of the EM wave I try the following: First I calculate the kinetic energy from the 90 degrees turn of the circular coil Then I try to find the amplitude of the EM wave and uses the theory for the radiation pressure above along with E=pc: Is this a wrong usage of the radiation pressure? -
First I will add some theory Then I will try to derive rydberg energy formula from a kinetic perspective The numbers above is correct for the rydberg formula. Is it possible to derive plancks constant, bohr radius or velocity for electron in n=1 for hydrogen atom with this? This is how far I get equating centripetal force and coulomb attraction:
-

attempting to isolate frequency of an EM-wave
Tor Fredrik replied to Tor Fredrik's topic in Classical Physics
-

attempting to isolate frequency of an EM-wave
Tor Fredrik replied to Tor Fredrik's topic in Classical Physics
In the theory aove they calculate the perturbation of an E-field. Since there is kinetic energy involved I thought perhaps that the energy also could be emitted as an EM-wave. The issue is that they dont adress the mass of the moving part of the infinte sheet. If that mass was known one could use kinetic energy as well. Then I have for equalities: Is it possible to isolate them for h without having f or B as a variable? -

attempting to isolate frequency of an EM-wave
Tor Fredrik replied to Tor Fredrik's topic in Classical Physics
Is there a way to calculate this? -

attempting to isolate frequency of an EM-wave
Tor Fredrik replied to Tor Fredrik's topic in Classical Physics
Well with my calculations there would be a formula for finding frequency f without using E=hf? But I needed clarifications since the solutions to maxwell dont directly tell me how to quantify its energy. -

attempting to isolate frequency of an EM-wave
Tor Fredrik replied to Tor Fredrik's topic in Classical Physics
well I thought E=hf is only valid for photons? -

attempting to isolate frequency of an EM-wave
Tor Fredrik replied to Tor Fredrik's topic in Classical Physics
well what if we just stopped an electron with kinetic energy and then equated this as the energy of the EM-wave released? -
the theory above from physics stack exchane made me puzzle a little One set of possible solutions to maxwell equations are It is known that deacceleration of an electron creates EM-waves. If you have a constant acceleration of an electron from a B field and stops the electron then all kinetic energy should be given out as an EM-wave so that Anyone have anything to add of an experiment that could determine the frequency this way?
-
In the example 5.11 above I don't understand how they revert to the natural coordinates while going from (5.68) to (5.69). In (5.68) the direction is along the y-axis. In (5.69) it follows the angle that goes round the sphere. But this angle is normal to y when it is at the y axis and parallell to the y axis while it is at the x-axis. How is it possible to revert between the y-axis in (5.68) and the angular axis in (5.69)?
-
I did stumble upon a thing about gauss law I guess this could explain that the sum of div of E inside the whole electron is as noted in gauss law But as for deriving without using gauss law? I think this problem in Griffiths might help I guess I just would have to read the answer properly
-

usage of vector identity in int to electrodynamics griffiths
Tor Fredrik replied to Tor Fredrik's topic in Classical Physics
I found it but thanks anyway. -
But in the orange part in my first post in this thread they use that thet get a value for the volume integral at origo and that it is 0 everywhere else. Yes luckily I did find my table. I see now that the requirement in the proof for gauss divergence theorem was that the volume must be continuous. So they are not mentioning F. So is it possible to prove that F does not have to be continous from the fundamental theorem of calculus? For example this note might pull one in the right direction?
-
In 5.55 they use Gauss law. In my proof of Gauss law they require that there is no holes on the volume of Gauss law. But in 5.55 there is a hole when the radius is 0. How can you create a proof for this rewriting then? I have the same issue in the electromagnetic gauss law: Then they introduce Gauss law even though the electric field E is undefined in origo I guess I in the end must add a derivation for Gauss law so that someone can point out how the proof is still valid for the theory above.
-
they refer to a product rule 5 for the second last equality above. This text is taken from David Griffiths, introduction to electrodynamics. If anyone is familiar with the book. At what page is product rule 5 that is used here introduced? I cant find that page. Or does anyone have another book or a internet site where this product rule 5 is derived? Or does anyone want to derive the second last equality above here on this page? On a further note I understand that So I understand how they obtain the left side of:
-

proof that in general curl of B field is uJ
Tor Fredrik replied to Tor Fredrik's topic in Classical Physics
Why would that lead to that the divergence of the current density is 0. Can you show it mathematically? -
Above they derive that curl of B is uJ. I know they use the identity So since as underlined above that the derivatives of J is 0 we have that But my problem is why is the derivative of J 0 in general. I have looked at a derivation for this: And the end of this derivation is the following But in the derivation they use that acceleration is constant and that it is a function of E showed in the orange box above. But E does not have to be constant since it is a function of r? So how is this a general derivation for the fact that divergence of current density is 0?
-
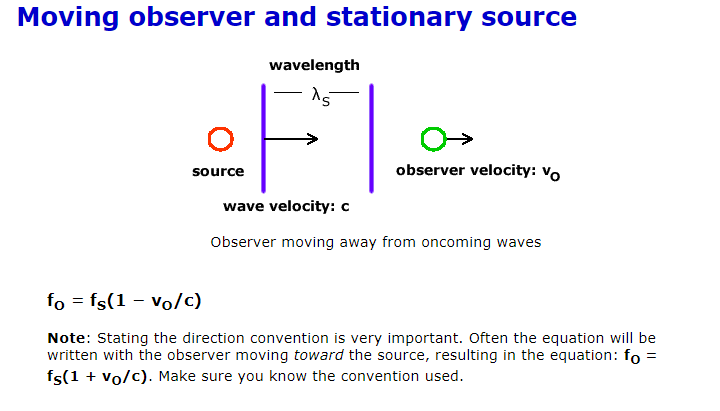
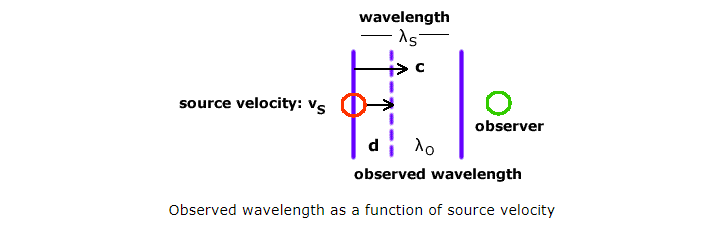
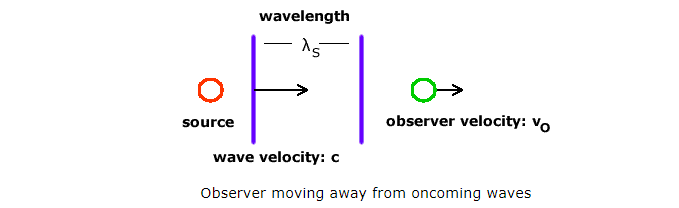
I have wanted to edit the post above. But since I have not managed to edit I will write an update. Further derivation for the frequency is 'so if a photon between the two mirrors are moving then we would get for the mirror that moves away from the photon As for the other mirror I am not sure. It does move away from the photon as well but (1) uses toward the source. And why are there two photons needed for this derivation? In short I am a bit lost over the energy translation here between the two mirrors and the photons. I am aware that they use p=E/c introduced by Maxwell.
-
Thanks for all the response. I have moved on and looked at a different derivation that uses E=hf. The formula that I have derived for the doppler shift formula is for this case gives this corrected wavelength And this case gives this observed wavelength But is this applicable to the momentum formula in (1). And how do they use plancks constant h in the momentum approxiamtion to the left of (1). Can someone derive this momentum approximation if possible?
-
I have tried to work on a derivation. Here is what I obtained. But my problem is how to get from an arbitrary velocity v to the speed of light.