mathspassion

we took here 123,456.....

not 123,234,345.....mean no repaeting of digit.

my question is why for this........ always 6(sum of digits) at the end.

For example

123=6

234=9

345=12=3

456=15=6

567=18=9

678=21=3

789=24=6 at the end sum of digits repaeating.

and if we do with one more example

12=3

23=5

34=7

45=9

56=11=2

67=13=4

78=15=6

89=17=8

910=19=10=1

1011=21=3 at the end sum of digitis repeating.

Numbers are amazing ,if we deep study about we get a lot miracle which we have to bring out ,in this view one more article see and observe why is it so……….why always 6.

(2,2,3....2,2,3......)

123-----1+2+3=6=0+6=6

456-----4+5+6=15=1+5=6

789-----7+8+9=24=2+4=6

101112----10+11+12=33=3+3=6

131415-----13+14+15=42=4+2=6

161718-----16+17+18=51=5+1=6

192021-------19+20+21=60=6+0=6

222324------22+23+24=69=15=1+5=6

252627------25+26+27=78=7+8=15=1+5=6

282930-----28+29+30=87=8+7=15=1+5=6

313233------31+32+33=96=9+6=15=1+5=6

343536------34+35+36=105=1+0+5=6

373839------37+38+39=114=1+1+4=6

404142------40+41+42=123=1+2+3=6

434445------43+44+45=132=1+3+2=6

464748------46+47+48=141=1+4+1=6

495051-----49+50+51=150=1+5+0=6

525354-----52+53+54=159=1+5+9=15=1+5=6

555657-----55+56+57=168=1+6+8=15=1+5=6

585960----58+59+60=177=1+7+7=15=1+5=6

616263----61+62+63=186=1+8+6=15=1+5=6

646566----64+65+66=195=1+9+5=15+1+5=6

676869----67+68+69=204=2+0+4=6

707172----70+71+72=213=2+1+3=6

737475---73+74+75=222=2+2+2=6

767778---76+77+78=231=2+3+1=6

798081---79+80+81=240=2+4+0=6

828384---82+83+84=249=2+4+9=15=1+5=6

858687---85+86+87=258=2+5+8=15=1+5=6

888990---88+89+90=267=2+6+7=15=1+5=6

919293---91+92+93=276=2+7+6=15=1+5=6

949596---94+95+96=285=2+8+5=15=1+5=6

979899---97+98+99=294=2+9+4=15=1+5=6

100101102--100+101+102=303=3+0+3=6

103104105--103=104+105=312=3+2+1=6

106107108—106+107+108=321=3=2+1=6

109110111—109+110+111=330=3+3+0=6

copyright to PiyushGoel

bare links removed by moderator

http://gonitsora.com/author/piyush/

sir whatever you trying to write i also know but i just try to prove hw it is .........

sir figure is right AB=3,AC=4 AND BC=5

as per figure find DE=?

only two seconds question if you know the particular theorum which recently obtained by .....................

thnxs Happy New Year 2017 to all my math lovers.......

ok wow gr8

Two Numbers (10 a+b) and (10 x+y)

For two digits numbers, numbers can be written in four ways like this


1. (10 a+b) and (10 x+y)

2. (10 a+b) and (10 y+x)

3. (10 b+a) and (10 x+y)

4. (10 b+a) and (10 y+x)

Multiple with each other

 (10 a+b)*(10 x+y) = 100 ax + 10 bx + 10 ay +by

 (10 a+b)*(10 y+x) = 100 ay + 10 by + 10 ax + x b

 (10 b+a)*(10 x+y) = 100 bx + 10 ax + 10 by + a y

 (10 b+a)*(10 y+x) = 100 by + 10 ay + 10 bx + ax

Subtract each one respectively

1.100 ax +10 bx + 10 a y + by - 100 a y - 10 by- 10 ax - x b = 90 ax + 9 bx -
90 a y – 9 by = 9(10 ax+bx-10 a y- by)
2.100 ax +10 bx + 10 ay + by – 100 bx – 10 ax- 10 by - a y = 90 ax - 90 bx
-9 a y – 9 by = 9(10 ax-10 bx- a y-by)
3.100 ax +10 bx + 10 a y + by – 100 by – 10 a y- 10 bx - ax = 99 ax – 99 by
= 9(11 ax -11 by)
4.100 a y + 10 by + 10 ax + x b -100 bx - 10 ax -10 by –a y = 99 ay -99bx =
9(11 a y-11 b x)
5.100 a y + 10 by + 10 a x + x b -100 by - 10 a y -10 b x –ax = 90 a y -90 by+
9 ax -9 x b = 9(10 a y-10 by +ax –x b)

For example

25 & 32, we can write them in four ways like 25, 32, 52 and 23and now multiple with each other like this

(25*32),(25*23),(52*32) and (52*23)
25*32=800
25*23=575
52*32=1664
52*23=1196
1664 – 1196 = 468 =4+6+8 =18 =1+8=9
1664 – 800 = 864 =8+6+4 =18 =1+8=9
1664 – 575 = 1089=1+0+8+9=18 =1+8=9
1196 – 800 = 396 =3+9+6 =18 =1+8=9
1196 – 575 = 621 =6+2+1=9
800 – 575 = 225 =2+2+5=9

Nine always Remain

is it for 345 only or for 5 12 13 as well.....

my mean is to everyone can solve it (it is still too lengthy) , it can be too short if you know there is a new formula recently obtained.

study deep

In a Right angle triangle ABC

AB=3,AC=4 & BC=5

at BC,E is middle point and D is altitude AD

Find distance DE=?

it is not a difficult question eveyone who know maths can solve easly but question is solve it in one line...........

ok you know how difficult upto the power 6 for this .................as per figure 16 lines shows how much work done by.......

some more work still pending ........pl wait......

never say rough working everthing has own existence whatever we do never go waste it reacts......it,s one own choice who play with numbers others with n power ........................

as the work done in digits upto 6 power like that you did ............................wow gr8

in the form of equations everyone says i have done.....................

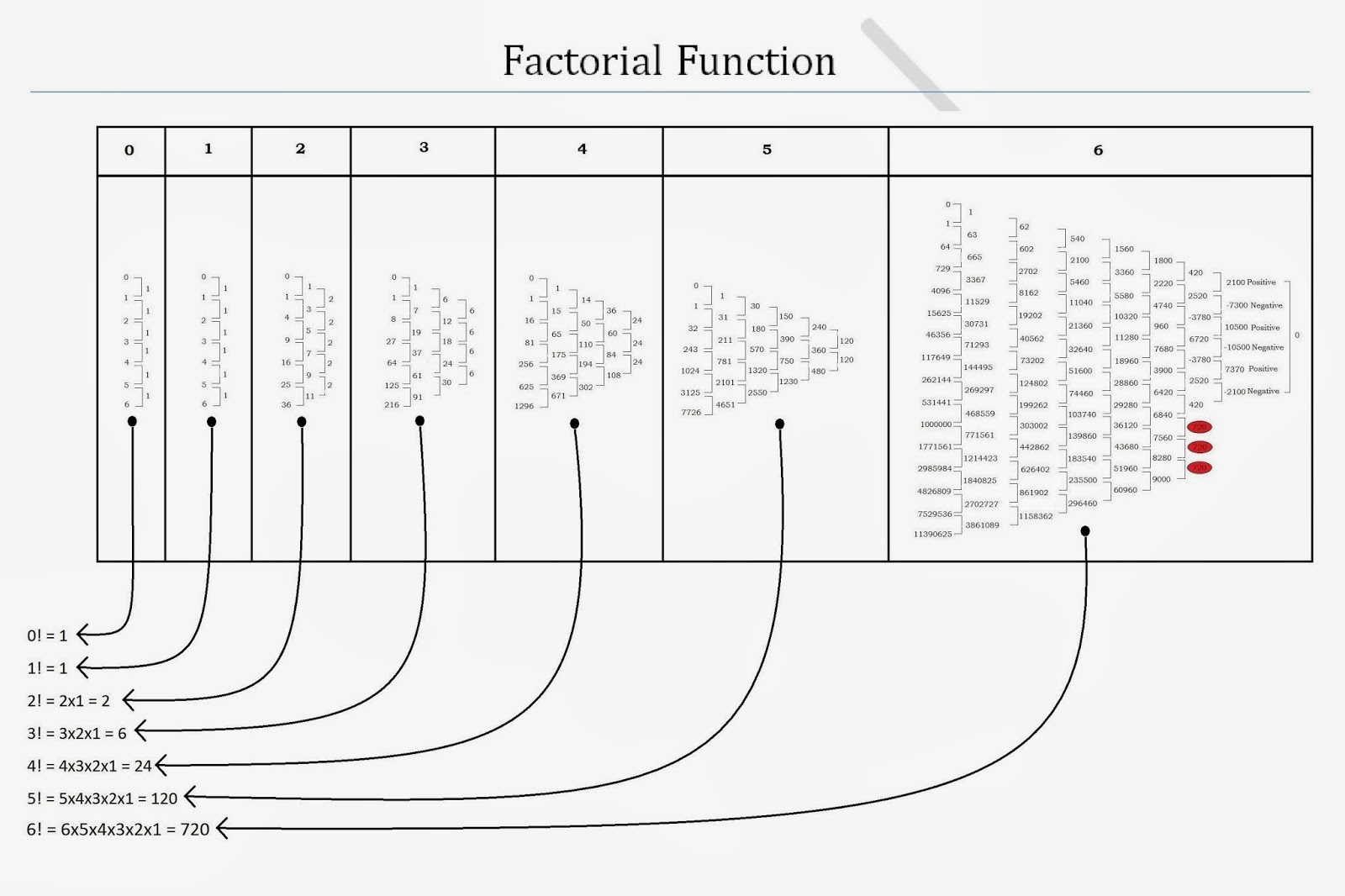
Today we will see how Piyush Goel discovered something while playing with numbers. Here is the story .

One day while sitting idle, and having nothing important to do he was just scribbling on paper. he was writing random numbers and thinking how could link them. To his amazement he discovered this:

he wrote down 0, 1, 2, 3, 4, 5.

Next to each number he wrote their respective squares, viz. 0,1, 4, 9, 16, 25.

Then start subtracting each successive square from the next bigger square.

It looks something like this: (1-0), (4-1), (9-4), (16-9) and (25-16).

What is the result?

he got 1, 3, 5, 7, 9.

Now again subtract each successive number from the next one in the order.

We are performing this: (3-1), (5-3), (7-5) and (9-7).

Surprisingly, he got (2, 2, 2, 2). A 2 in each case. he was amazed and decided to take a step further. This time with cubes.

So here go my numbers 0, 1, 2, 3 ,4, 5, 6.

And their respective cubes: 0, 1, 8, 27, 64, 125, 216.

Time to perform first round of successive subtraction, i.e. (1-0), (8-1), (27-8), (64-27), (125-64) and (216-125). The result: 1, 7, 19, 37, 61, 91.

Second round of successive subtraction as performed earlier: (7-1), (19-7), (37-19), (61-37) and (91-61).

And this is what he got: 6, 12, 18, 24, 30.

Successive subtraction performed the third time: (12-6), (18-12), (24-18) and (30-24).

And this time he got the result (6, 6, 6, 6).

You see, squaring means ‘to the power 2’ and he got the result 2 after 2 successive subtractions, which is the value of 2!

Cubing means ‘to the power 3’ and after performing 3 successive subtraction he got 6 in each case which is nothing but the value of 3!

He similarly performed with 4th and 5th powers of the first few whole numbers. He was surprised to find the final value of 24 and 120 which are of course the values of 4! and 5!.

It was all right up to 5, but he wanted to go a notch higher and check for 6 just for my personal satisfaction. While doing for 6th power the calculations were massive and numbers so huge that it took him a couple of hours to do his calculations. Just to be sure he also did it for numbers upto 15.

Put 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14 and 15 and their respective 6th powers:

0,1,64,729, 4096, 15625, 46356, 11649, 262144, 531441, 1000000, 1771561, 2985984,4826809, 7829536 and 11390625.

He kept on doing successive subtractions till to his contentment he finally got 720 for all which is the value of 6!

With little efforts, we can work out algebraic relationship for the above but leave it for some other time.

gonitsora.com a very useful site..

yes know but if we go deep we get something new..........

now your turn....... find more.........

Symmetry of Digit "2" In Squaring

If we square 11, it is very simple put 1(2*1) (12) get 121 same as square 12 put 1(2*2)(22) get 144 again for 13 we get 169 and for 14 we get 1 8 16=196 and so on.

When we go deep, we find that there is symmetry of two types

(2, 4, 6, 8, 10, 12, 14, 16, 18, 20 …. Diff is always 2) &

(1, 4 , 9 , 16, 25, 36, 49, 64, 81, 100 ) diff. is 3 5 7 9 11 13 15 17 19 and diff. of 3 5 7 9 11 always 2, so there is true symmetry .

Up to 19 it is right but at 20 how we can put 1 20 100 just because of symmetry.

• 112 = 1 2 1

• 122 = 1 4 4

• 132 = 1 6 9

• 142 = 1 8 16 = 100 + 80 + 16 = 196

• 152 = 1 10 25 = 100 + 100 + 25 = 225

• 162 = 1 12 36 = 100 + 120 + 36 = 256

• 172 = 1 14 49 = 100 + 140 + 49 = 289

• 182 = 1 16 64 = 100 + 160 + 64 = 324

• 192 = 1 18 81 = 100 + 180 + 81 = 361

• 202 = 1 102 = 1 20 100 = 100 + 200 + 100 = 400

• 212 = 1 112 = 1 22 121 = 100 + 220 + 121 = 441

• 222 = 1 122 = 1 24 144 = 100 + 240 + 144 = 484

• 232 = 1 132 = 1 26 169 = 100 + 260 + 169 = 529

• 242 = 1 142 = 1 28 196 = 100 + 280 + 196 = 576

• 252 = 1 152 = 1 30 225 = 100 + 300 + 225 = 625

• 262 = 1 162 = 1 32 256 = 100 + 320 + 256 = 676

• 272 = 1 172 = 1 34 289 = 100 + 34 + 289 = 729

• 282 = 1 182 = 1 36 324 = 100 + 360 + 324 = 784

• 292 = 1 192 = 1 38 361 = 100 + 380 + 361 = 841

• 302 = 1 202 = 1 40 400 = 100 + 400 + 400 = 900

There is a symmetry, a method, which is shown as below for 31, 41, 51 and so on.

• 312 = 1 212 = 1 42 (1 11)2 = 1 42 (1 22 121)

= 961 = 121 + 220 + 100

= 441 + 420 + 100 = 961

• 412 = 1 312 = 1 62 (1 21)2 = 162 (1 42) (1 11)2

= 1 62 (1 42) (1 22 121)

= 1 62 (961) = 961 + 620 + 100 = 1681

• 512 = 1 412 = 1 82 (1 31)2 = 1 82 (1 62) (1 21)2

= 1 82 (1 62) (1 42) (1 11)2

= 1 82 (1 62) (1 42) (1 22 121)

= 1 82(1681) = 1681 + 820 + 100 = 2601

• 612 = 1 512 = 1 102 (41)2 = 1 102 (1 82) (1 31)2

= 1 102 (1 82) (1 62) (1 21)2

= 1 102 (1 82) (1 62) (1 42) (1 11)2

= 1 102 (1 82) (1 62) (1 42) (1 22 121)

= 1 102 (2601) = 2601 + 1020 + 100 = 3721

• 712 = 1 612 = 1 122 (1 51)2 = 1 122 (1 102) (41)2

= 1 122 (1 102) (1 82) (1 31)2 = 1 122 (1 102) (1 82) (1 62) (1 21)2

= 1 122 (1 102) (1 82) (1 62) (1 42)(1 11)2

= 1 122 (1 102) (1 82) (1 62) (1 42) (1 11)2

= 1 122 (1 102) (1 82) (1 62) (1 42) (1 22 121)

= 3721 + 1220 + 100 = 5041

• 812 = 1 712 = 1 142 (1 612) = 1 122 (1 51)2 = 1 122 (1 102) (41)2

= 1 122 (1 102) (1 82) (1 31)2 = 1 122 (1 102) (1 82) (1 62) (1 21)2

= 1 122 (1 102) (1 82) (1 62) (1 42)(1 11)2

= 1 122 (1 102) (1 82) (1 62) (1 42) (1 11)2

= 1 122 (1 102) (1 82) (1 62) (1 42) (1 22 121)

= 5041 + 1420 + 100 = 6561

• 912 = 1 812 = 1 162(1 712 ) = 1 142 (1 612) = 1 122 (1 51)2

= 1 122 (1 102) (41)2 = 1 122 (1 102) (1 82) (1 31)2

= 1 122 (1 102) (1 82) (1 62) (1 21)2

= 1 122 (1 102) (1 82) (1 62) (1 42)(1 11)2

= 1 122 (1 102) (1 82) (1 62) (1 42) (1 11)2

= 1 122 (1 102) (1 82) (1 62) (1 42) (1 22 121)

= 6561 + 1620 + 100 = 8281

• 1012 = 1 912 = 1 182(1 812) = 1 162(1 712 ) = 1 142 (1 612) = 1 122 (1 51)2

= 1 122 (1 102) (41)2 = 1 122 (1 102) (1 82) (1 31)2

= 1 122 (1 102) (1 82) (1 62) (1 21)2

= 1 122 (1 102) (1 82) (1 62) (1 42)(1 11)2

= 1 122 (1 102) (1 82) (1 62) (1 42) (1 11)2

= 1 122 (1 102) (1 82) (1 62) (1 42) (1 22 121)

= 8281 + 1820 + 100 = 10201

This is a short guide to using the new LaTeX system that has been implemented on the boards. First off, for those who don't know what LaTeX is, a short description. LaTeX is, to all intents and purposes, a fully fledged math typesetting system - basically put, you can write math with it. It's a very flexible and hence very advanced piece of software, and the syntax for it is quite complex, but fairly easy to learn for typesetting smaller equations.

 

On scienceforums.net, we've implemented a small LaTeX system to allow you to typeset equations (in other words, cut out all the x^2 stuff and make things easier to read for everyone). The basic principle behind it is this: you have a LaTeX string, and you surround it by [math][/math] tags. I'll come to the syntax of the actual string in a moment.

 

For those who can already use LaTeX (and indeed, those who can't), a few things to note. In the system we've implemented, a tex file is created, surrounding the string you input with a \begin{display} environment so there is no need for $, $, \[ etc. Also note that we've included the standard AMS files for you; if anyone wants any special characters, I'm sure we can probably accommodate your needs.

 

The images are clickable, so you can see the code that was used to make them by clicking.

 

Now that's all out of the way, onto some examples

 

Examples

 

[math]x^2_1[/math] - Indexes (both subscript and superscript) on variables

 

[math]f(x) = \sin(x)[/math] - A simple function.

 

[math]\frac{dy}{dxx} = \frac{1}{1+x^2}[/math] - Example of fractions - you can create small fractions by using \tfrac.

 

[math]\int_{-\infty}^{\infty} e^{-x^2} = \sqrt{\pi}[/math] - A nice integral.

 

[math]\mathcal{F}_{x} [\sin(2\pi k_0 x)](k) = \int_{-\infty}^{\infty} e^{-2\pi ikx} \left( \frac{e^{2\pi ik_{0}x} - e^{-2\pi ik_{0}x}}{2i} \right)\, dx[/math] - a Fourier Transformation, which is rather large.

 

I could go on and on, but I'll go onto explain some of the basic syntax of LaTeX.

 

Syntax

 

Functions & General Syntax

 

Basically put, if you want to write a math equation in LaTeX, you just write it. If you wanted f(x) = 3, then bung that between to math tags and you're done, producing [math]f(x)=3[/math]. Don't worry about extra spaces or carriage returns, because in general LaTeX will ignore them. It does get a little more complex than this, but don't worry about that for now. Remember that any letters you type in will be presumed to be some kind of variable and hence will be italicised.

 

We also have functions to display more complex things like matrices and fractions, and they have the syntax of having a \ before them, usually followed by some kind of argument. For example, \sin will produce the function sin and \frac{num}{denom} will produce a fraction with a specified numerator and denominator. More on these later.

 

Also remember that LaTeX is case sensitive, so \sigma is NOT the same as \Sigma.

 

Subscripts and Superscripts

 

This is perhaps one of the easiest things to do in LaTeX, and one of the most useful. Let's, for the sake of argument, say you wanted to write x². Then you'd write x^{2}, producing [math]x^2[/math]. Notice that you don't necessarily need the { and } in cases where you only have 1 thing in the index, for example x^2. But it does care if you want to write something like [math]x^{3x+2}[/math]. Subscripts are done similarly, but you use the _ operator instead of ^. If you want both subscript and superscript, then use the syntax x^{2}_{1} - which is equivalent to x_{1}^{2}.

 

Fractions and functions

 

As I've mentioned, fractions are generated by using the function \frac{num}{denom}. For example:

 

[math]\frac{1}{3}[/math]

 

[math]\frac{7}{x^2}[/math]

 

If you want smaller fractions, you can use \tfrac, to produce things like [math]\tfrac{1}{2}[/math] which will fit into a line nicely without having to seperate it.

 

LaTeX has some nice in-built functions like \sin, \cos, etc. I'm not going to write them all down here, but I'll point you to a website at the end of the document that contains them. Likewise, you can write symbols (such as infinity by using \infty) and Greek letters (e.g. \phi, \Sigma, \sigma, etc)

 

Bracketing

 

You can get all your usual brackets just by typing them straight in; for instance, (, |, [, etc. However, sometimes they won't be the right size, especially if you want to write something like (1/2)ⁿ. You can get around this by using the \left and \right commands, and then placing your favourite brackets after them. For instance, to write (1/2)ⁿ, we have:

 

[math]\left( \frac{1}{2} \right)^{n}[/math]

 

Integrals, Summations and Limits

 

Integrals can be produced by using \int, summations by \sum and limits by \lim. You can put limits on them all in the right places by using the normal subscript/superscript commands. For instance:

 

[math]\int_a^b x^2 \,dx[/math]

 

[math]\lim_{n\to\infty} \frac{1}{n} = 0[/math]

 

[math]\sum_{n=1}^{\infty}\frac{1}{n^2} = \frac{\pi^2}{6}.[/math]

 

Summary

 

There's a lot more things you can do with LaTeX, and I'll try to add to this as time goes by. Have a look at:

 

http://www.maths.tcd.ie/~dwilkins/LaTeXPrimer/'>http://www.maths.tcd...ns/LaTeXPrimer/ - the LaTeX primer

http://omega.albany.edu:8008/Symbols.html'>http://omega.albany....08/Symbols.html - some symbols that you might find useful.

 

If you have any questions about the system, send me a PM and I'll try to help

 

Cheers.

great