Celeritas

I meant only that twin B maps the twin A clock in his own spacetime system, as he goes. If he had a tracking console, it would be populated on the display because it's current location is being updated and calculated. You say B measured the current A clock location and readout as he goes. But that's impossible. He's remote from A, and must consider the light transit time, the speed of light, and determine the A velocity and A location (as he goes) per whatever model he uses. One may be able to prove B wrong, depending on how he is figuring it all. Maybe you can, maybe you can't ... We might imagine other clocks crossing paths during B's roundtrip. Does B predict the correct readout of those clocks when they intersect, or not? The owners of those clocks could verify that. Which theory predicts that accurately? If both do, then I'd say there is no way to know (yet) if one theory matches reality and the other does not. For example, assume for a moment that the 1-way = 2-way in nature. If conventions using 1-way <> 2-way produce the same solns, then both theories are valid far as spacetime solns are concerned, however only 1 theory matches what is real. We cannot measure the 1-way speed of light, and so I figure we may never know the answer to that. LET theory could be correct, or SR could be correct. There may well be various reasons though, for presuming one theory superior to the other, but there may be no known way to ever prove that. Then, Occam's Razor says use the simplest theory, and that theory is the most likely to match mother nature (but not guaranteed to). I think Einstein picked 1-way = 2-way because it produces the simplest derivation and the simplest transforms. Also, since he was not commencing his derivation from a master frame, it seems to me that 1-way = 2-way would be the natural first choice. It would always be the natural first choice, if starting from a master frame or not. I figure he would not say that his convention was the most likely to match reality, as he could not prove it. Best regards, Celeritas

But I was speaking strictly of how the A clock exists "in the B spacetime system" over the round trip, to determine A's aging. Not "seeing" the hands of the A clock as B goes. Again, using everyone's proper time alone (per each themselves), produces the correct relative aging, and is the easiest approach. No dispute there. My point has been that B should be able to accurately predict the extent of twin A aging, using only A-coordinate values (per B), using the MCCIRF method. And, we could imagine a well preplanned flight test. Twin B cannot ignore how A exists in B's own spacetime system during his turnabout. If he does ignore it, B will predict A to age only 3.2+3.2=6.4y (not 10y) on reunion. That's wrong, only because it's incomplete. When I say sense-of-simultaneity, or sense-of-now across space, I mean line-of-simultaneity. If "sense" is a problem, just assume I said B's "simultaneous space", instead of B's sense-of-simultaneity. That's fine md. Nobody has a problem with the Time Handoff scenario, and it's certainly the simplest case. However, I've only been trying to point out what I mentioned above, in the 3rd para of my first response above. All good points, and I've been trying to do so. I've never worked on this before. There's a learning curve, as I go. For any two clocks momentarily intersecting in spacetime, they have a specific set-of-readouts. SR makes its prediction. Any valid theory must predict the correct readouts, and the owners of those 2 clocks know what their clocks then read. All in the cosmos must agree, if the transformations they use are valid. I'm primarily looking to see what changes in convention cause a change in that set-of-readouts (wrt SR), versus what changes do not. Best regards, Celeritas

It was late when I posted last night, and I suppose "and components of them" was vague. The 1-way speed of light has never been verified by test, and may never be. So until it is, it's certainly fair to say that a convention used is a personal preference. It cannot be known that it represents something true in nature. I should add, while (say) Lorentz Ether Theory (LET) uses the same time sync procedure as SR, the meaning of "in sync" means something different for LET vs SR. In SR, you are assumed in sync after running the procedure, however in LET your assumption of such is mistaken while yet unawares. Philosophically, one theory (eg Lorentz Ether Theory, LET) may assume a master frame, while the other (eg SR) does not. One theory (LET) possesses a much more convoluted meaning than does the other (SR). So while they use the very same LTs, they mean something different. Light signals cannot prove which theory is right. So, it's a philosophical choice as to which theory one prefers. A block universe and a master ether frame are two such philosophical choices. Eternalism and Presentism are philosophies of spacetime. So, I agree in all that. The important thing, is that any valid theory (of space and time) must accurately predict the time readout of moving clocks upon flyby, anywhere and everywhere in spacetime. And, we may imagine virtual clocks of all frames at all points in spacetime, with virtual clocks replacable by real clocks. What is real, are the measurements and the predicatability of theories per measurements. With enough consistency of predictability, mathematically sound theories are then accepted. I'm still of the opinion that the accrual of twin A coordinate time must match the accrual of twin A proper time. If twin B does NOT consider the accrual of twin A coordinate time during his turnabout, then twin A ages only 3.2+3.2 = 6.4y over the interval (which is wrong, because it's incomplete). If twin B DOES consider it, then twin A ages the required 3.2+3.6+3.2 = 10y over the interval, which matches the proper time accrual of twin A. This is only to say that the present coordinate time of a remote moving clock is the proper time of that clock at that spacetime location, and while the use of coordinate time is less convenient it is no less correct. During turnabout, the fact that B's added consideration of twin A coordinate-time produces the total required aging of twin A (10y), lends weight that the rapid advancement of the A-clock readout (in the B system) is valid and representative of something real, just as proper time is assumed representative of something real. Just for a moment ... let's assume that all moments in time coexist in a fused spacetime continuum. IOW, let's assume that particular philosophy matches reality. As such, the wild advancement of the A clock in the B system during turnabout, is the result of a real mechanism, not (say) a mere mathematical artifact. The current readout of a remote moving clock then depends upon where your sense-of-simultaneity then slices the twin A worldline, and said intersection dynamically changes while transitioning inertial frames of reference (eg B's turnabout). Your sense-of-simultaneity is governed by the angular orientation of your spacetime system in spacetime which is dependent on your current velocity, and is dynamic during proper acceleration. So, it would then model what is real. Also, the rapid advancement in A-clock coordinate time has no impact on twin A, just as turning your head has no impact on the stars in the night sky. It's only a change in POV of the observer. Twin A always experiences the passage of time as completely normal, ans everyone else does. Lastly, I'm still studying the impact of differing time sync conventions, and I'll need more time before saying more in that regard. And as you (md) had mentioned, I'm not even sure (as yet) that these differing conventions make sense, or whether all the assumptions used in their derivation even make sense. It's been somewhat a challenge. One thing is for certain, if no convention can be proven true to nature, then you'd have to be a mascocist to use a non-midpoint reflection event. Best regards, Celeritas

Agreed md, the LT derivation was based on a kinematic model. My point, was only to say that an instant acceleration is unrealistic, and anything less than instant "allows for continuity of" the A clock in the B spacetime system during his turnabout. It's not so easy to ignore it, if not instantaneous. You've argued that only proper time should be considered, because its absolute, while coordinate time is relative per POV. My point has been that coordinate time of a remote clock at a point in spacetime, is the proper time of that clock at that location in spacetime. Upon B/C flyby, each predict a different time of the A clock, but this does not mean they are wrong. They are both correct, and the eventual receipt of light signals will confirm that. As such, there is no reason (in my thinking) that the accrual of clock A coordinate time (per twin B) should not match the accrual of proper time (per A), ie 10y-A. And it does, and makes complete sense, using (for example) the MCCIRF method. It's certainly not the convenient method, but just as correct. If B ignores his turnabout, he must predict that twin A ages only 3.2+3.2 = 6.4y-A. However, we know he must age 10y-A. Therefore, the twin A existence in the B spacetime system during turnabout, cannot be ignored (instant turn, or not). The X clock reads 5y-A during twin B's complete turnabout, because no time can pass per anyone in the cosmos in an instantaneous turnabout (by definition). Well, if B had no idea of relativity theory, he'd calculate the Newtonian predictions as he went. He'd be wondering how he got to planet X as fast as he did, with no good explanation. He'd be confused until he figured out how to derive the LTs In thought experiment, the sweep at A may be logically deduced. The eventual receipt of light signals verifies LT solns for any and all spacetime events in all-inertial scenarios. Now, imagine a clock D colocated and comoving with B. Twin B makes his turn at planet X, but D keeps on coasting. The eventual receipt of light signals will prove to D that when B turned, the A clock was 2.4 ly downrange and read 3.2y-A. That's a valid test. The B clock made that same prediction at the turn, so he was right, as confirmed by D's eventual verification. Next, B instantly lands on planet X. The eventual receipt of light signals will confirm that upon landing, twin A was 3 ly downrange with a readout of 5y-A. That's a test. So either the A clock truly advanced from 3.2y-A to 5y-A in no time at all (due to POV chnage), or it jumped in readout by magic, or B's SR prediction of the A clock readout while inertial is flawed (and Newton was right all along). The current A clock readout depends only on the current POV. When B transitions frames of reference at turnabout, his POV dynamically changes wrt those who remain inertial. His POV changes because his spacetime system rotates in 4-space. His sense-of-simultaneity rotates as his spacetime system rotates. The current A clock readout (and location) depends only on where B's sense-of-simultaneity then intersects the A worldline. Since his spacetime system dynamically rotates during turn, the remote A clock wildly swings in readout (and location). This has no affect on twin A or his clock, who always experiences time to pass steadily as normal. Turning your head at night, has no impact on the stars themselves. It's a POV change. What's required, is that all moments in time coexist, as inches on the ruler do. Ie, a fused spacetime continuum. That all worldlines are laid out in the continuum in their entirety, eternal in a sense. That we for reasons unknown, we do not experience that directly, however the measured relativistic effects (to date) are the proof of it. The required time desynchronization of moving bodies, is a clear example of why it should exist as such, IMO. But ... All that said, Lorentz's version of relativity (as re-interpretted after 1905) possesses the very same LTs, but means something completely different. It also uses the same time synchronisation procedure. Also, coordinate time means something different in Einstein's theory, versus Lorentz's theory. Therefore, I'll have to agree that the meaning of theories, and components of them, is subject to philosophical choice. The measurements, and noted predictability, are not. Does that sound fair md? Best regards, Celeritas

md63356, BTW, wrt my derived transformations for the case (2), where ... ..... 0 < e < 1 ..... cout ≠ cback ..... and where e ≠ ½ ........ ... (where e = ½ would be the SR convention) Considering the A and B worldlines from A/B flyby to BC flyby (Time Handoff scenario), while the gamma factor remains at γ = 1/√(1-v²/c²) for the relation between the A & B clocks, it also turns out that moving contracted lengths at rest in the B frame (as noted by A) must contract to values different from 1/γ. No doubt, because cout ≠ cback ≠ c, and spatial-offsets from the B worldline produce different coordinate values (of B per A) than does SR. All this, makes it very clear why Occam's Razor should win, and Einstein's convention be assumed as "the most likely" true-to-nature. Alas, it seems impossible to ever prove such, or so it would seem today. Best regards, Celeritas

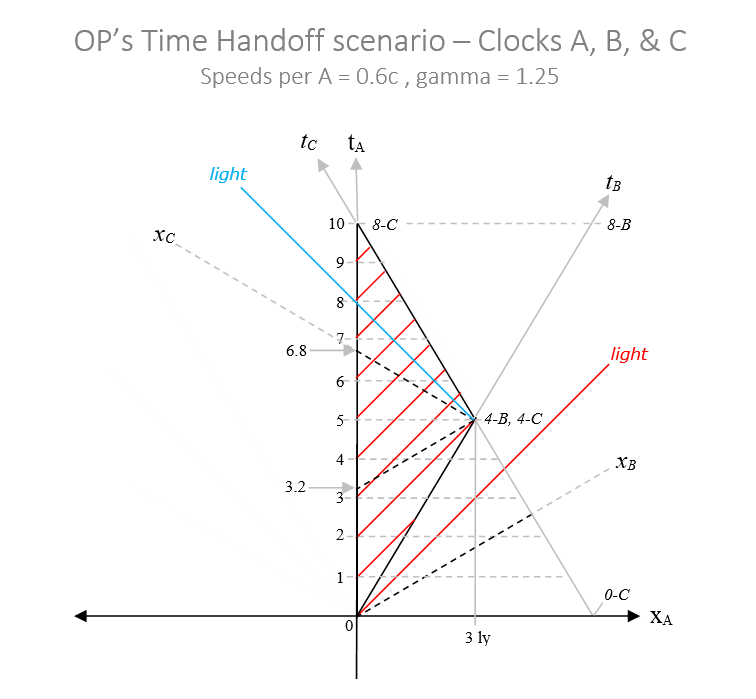
You had mentioned (prior) the momentarily co-moving and co-located inertial reference frames (MCCIRFs) that coincided with the twin B during his own own proper accelerations. At any moment during B turnabout, the local speed of light from A should be speed-c per twin B and the corresponding MCCIRF, and they should also agree on the doppler shift of the light from twin A. And, we may assume that we knew the frequency of the light transmitted by A per A in a pre-planned test event. Although, given superfast unrealistic proper accelerations by B, twin B may be required to coast momentarily to verify and validate that doppler effect. Consider this md ... We might imagine the twin's executing a pre-planned flight test precisely as we've been discussing here, with instant (or virtually so) B turnabout at a planet X. Planet X is at rest with earth, separated from earth by 3 ly proper, and it's clocks are synchronized with the earth (and twin A) clocks. Everytime the flight test is executed, the relative aging result is the very same, because the flight test is conducted identically every time. Next, imagine that at any point in time during the B turnabout at planet X, we have twin B "go to coast" and hence becomes inertial. Here, I am making a point as to "the validity of" the A clock sweeping continguously from 3.2y-A thru 5y-A to 6.8y-A (in the B system) during his turnabout (which I say is consistent with SR). Further, let's imagine that B is told to "go coast" precisely when he is momentarily co-moving and co-located with Planet X. The B clock then reads 4y-B, and twin B is now inertial. What do you think the twin B navigation system will declare of the current range to twin A (on earth), and for the current time on the clocks of planet X, earth, and twin A? Per B, I submit those clocks must then all read 4y, and with twin A 3 ly downrange. For that to happen, which I submit would be the only outcome consistent with SR (and reality), it must be true that the A clock contiguously swept from 3.2y-A to 5y-A in the B spacetime system during B's instant (or virtually instant) turnabout. Therefore, it must be true that the A clock contiguously swept from 3.2y-A thru 5y-A to 6.8y-A in the B spacetime system during B's instant (or virtually instant) turnabout, in the complete twins scenario we've been discussing here. Yes? Best regards, Celeritas

Well, I did not post the complete derivations, so that's understandable. I'm having some difficulty understanding exactly what they mean too. I derived transforms for 2 cases ... ... (1) 0 < e < 1 ... where 1-way = 2-way (speed-of-light) ... (2) 0 < e < 1 ... where 1-way <> 2-way (speed-of-light) ... unless e= ½ Case (1) seems improper IMO. The LTs are derived exactly as done in OEMB, with an invariant c, and closing rates of c-v (outbound) and c+v (inbound). Yet, to select a non-midpoint reflection event requires cout <> cback. So an invariant c and non-midpoint reflection event seem mutually exclusive. This is why I derived transforms for case (2). Case (2) determines the cout and cback for the selected e. My derivation seems proper, however I am not yet certain the 3 aformentioned assumptions that I made (during derivation) were proper. I must admit, the solns for a non-midpoint reflection event seem suspicious, but I'm still trying to understand it and verify it is actually right. I've been following your advice, in assuming that unexpected results may not necessarily be wrong. In fact, I'm still trying to convince myself that the derivation is logically sound, so this may take awhile. Fair enough md. You quoted "doesn't cause", and wonder regarding the precise meaning of that. Your prior point regarding "proper-time accrual" being the important (and easiest) thing, is certainly a cause for the relative aging. That speaks to the comparison of the 2 worldline lengths. However ... It is equally true that the proper accelerations (ie frame transitioning) by twin B allows that worldlines geometry to become attained. That's about it, IMO. It really comes down to relative simultaneity. I like to say the same thing just a little differently ... It's about the relative angular orientation between the spacetime systems, which in the twins scenario is dynamic ... which also allows for re-location for an absolute age comparison. One twin must depart the originating common frame, or there be no relative aging differential. He who properly accelerates to transitions frames, always ages the least. So the geometry defines the relation of the worldlines and their lengths, the worldline length(s) define the proper time(s) accrued, and B's proper acceleration creates the worldlines geometry with re-colocation. Very true, causality is dictated by locality, and hence by the transfer of light signals. I would only add that ... This does not then lead that when twin B executes his (instant, or virtually instant) turnabout, that twin A cannot sweep contiguously from 3.2y-A to 5y-A to 6.8y-A within the B spacetime system. Twin A must do so, if SR is correct. And IMO, that's the more interesting part. It matters not, that B does not "see this" via light signals. However, for the light received by twin B from twin A, the corresponding doppler shifts notable by twin B (during his transition of frames) provide a validation of this, per SR. The meaning of the theory seems incomplete IMO, if this point is not considered or understood. This is to say that when twin B arrives back on earth, before he even asks A to show his clock, B has already predicted that A must have aged 10 yr ... 3.2-A inertially out, 3.6y-A during instant (or virtually instant) turnabout, and 3.2y-A inertially back (=10y-A total). Each twin has each their own proper time accrual, but each twin also has their prediction of the other's aging over the common interval, and everyone's correct. Best regards, Celeritas

accidental post ... thanx, Celeritas

Update to my prior post, which is the 7th post back from here. My apologies. My previous derivation of the time transformation for a non-midpoint reflection event (with 1-way = 2-way speed-of-light) was missing a 1/c2 term, which produced the correct numeric result (given c=1) but with incorrect units. The space transformation (for x→x') was correct. .... (Eqn 1, old) ...... t' = γ[ (1/γ2 - (2ec-v-c)v)t - (v+(1-2e)c)x)/c2 ] ....... ← incorrect time transform (posted prior) .... (Eqn 1, fixed) ... t' = γ[ (1/γ2 - (2ec-v-c)v/c2)t - (v+(1-2e)c)x/c2 ] ....... ← correct time transform (posted here) .... (Eqn 1) ............. t' = γ[ (1/γ2+(v+(1-2e)c)v/c2)t - (v+(1-2e)c)x/c2 ] ....... ← I reorganized the corrected time t coefficients this way ) The correct transforms are as follows ... .... (Eqn 1) ... t' = γ[ (1/γ2+mv/c2)t - mx/c2 ] .... (Eqn 2) ... x' = 2eγ(x-vt) where … m = v+(1-2e)c where … 0 < e < 1 where … γ = 1/√(1-v²/c²) For e = ½ , the above transformations reduce to the LT's of Special Relativity. Best regards, Celeritas

md65536, This supercedes my prior related post. So it turned out to be a very silly misapplication of a parentheses in 1 spot. Couldn't believe it, but on the other hand, yes I can. My eyes were buggy from looking at pages full of parens. So with the correction (which applies to EQN 3 below), the spreadsheet shows it matches SR precisely for reflection event e=½, be it proper or coordinate values produced. It varies from SR the moment e <> 1/2, and it should. (1) e ... is a variable that specifies the point-of-reflection as percentage of the roundtrip, so 0 < e < 1. (2) I assume the 2-way speed of light is invariant c, but the outbound light speed (along +x) and inbound light speed (along -x) is determined based on the selected reflection event e. (3) Assumption I ... the linear coefficent alpha (that arises from integrating the partial derivatives eqn) is equal to a = 1/gamma, just as per SR. Einstein was able to deduce that a = 1/gamma per phi(v) = 1, but I could not do that because the transforms did not reduce much. Therefore, I just assumed what Einstein deduced, that a = 1/gamma. (4) Assumption II ... there's that point in the derivation where you plug the interim eqn for time Tau (T) into X = cT. However, what speed-of-light to use? The 1-way outbound, the 1-way inbound, or the averaged 2-way speed-of-light? The options are cout = c/(2e), cback = c/(2(1-e)), or c (=cround_trip) where c is the average 2-way light speed (invariant c). Well, I used cout = c/(2e) for the same reason Einstein substituted x'/(c-v) for t instead of t = x'/(c+v) ... so I used t = x'/(cout -v), and for X = cT I used X = coutT. I'm sure this derivation is correct, given the assumptions I made. How much use this is I do not know, but it is interesting to compare what happens for time sync conventions that differ from SR, and again, this matches SR for SR's e=0.5. Here's a repost of my most prior, with corrected space transform for x→X ... *************************************************************************************************** As derived from the 3 TAUs Eqn in OEMB Section 3, but where e specifies the reflection event ... ... 0 < e < 1 ............← Use e=0.5 to produce SR transformation solns ... e(T0 + T2 ) = T1 ... e [ T0(0,0,0,t0) + T2 { (0,0,0,t0 + x’/(cout -v)+x’/(cback+v) } ] = T1[ x’,0,0,t0 + x’/(cout -v) ] My interim substitutions were these ... ... where Einstein uses X=cT ... I used X = coutT ... where Einstein uses t = x'/(c-v) ... I used t = t = x'/(cout -v) ... and of course ... x' = x-vt The transforms attained were ... ... (Eqn 3) ... X = cout [ 1/(cout -v) - m/n ] (x-vt) / γ ... (Eqn 4) ... T = [ ( n + mv) t - mx ] / (γn) where … ... 0 < e < 1 ... cout = c/(2e) ... cback = c/(2(1-e)) ... m = [ (1-e)cback - ecout + v ] ... n = (de -v2) ... de = (cout*cback) + (cout-cback)v ... γ = 1/√(1-v2/c2) *************************************************************************************************** Thank you for the help md. Much appreciated! Best regards, Celeritas

md, Yup, I see exactly what you mean now. It's beat the crap outa me here. In my most prior derivation here, while I believe I have the time transform correct (t -> T), the space transform x -> X seems to be mistaken. Been looking at it, but I don't see the mistake yet. It may have to do with my 2nd assumption I had mentioned prior, not sure? The spreadsheet that processes the transforms produces the correct B values per A, but only for events ON the B worldline, and no matter what the reflection event (e) selected. However, when I set e=0.5 in the derived eqns, and reduce it by hand, it does not seem to reduce to the SR LT for X (it should). However, for any coordinate inputs that are off the B worldline, they certainly don't match the SR soln. But while I would figure them not to, I doubt my solns differ "properly". That said, I posted thinking it was right, but clearly I posted too quickly. If I figure it out, and am 100% certain, I'll repost it. I do see what you mean though, about too complicated, and whether it can even work. Thanx, Celeritas

md65536, So I did put a derivation together for this. It allowed a reflection event at 0 < e < 1, versus SR's midpoint reflection event of e = 1/2. It also assumes the 2-way speed of light is always c (ie averaged), but does calculate the required 1-way light speeds (outbound vs return) based on the selected e. I derive the transforms in the same manner as done in OEMB. However, I had to make 2 assumptions ... (1) the linear coefficent alpha (that arises from integrating the partial derivatives eqn) is equal to a = 1/gamma, just as per SR. Einstein was able to deduce that a = 1/gamma per phi(v) = 1, but I could not do that because the transforms did not reduce much. Therefore, I just assumed what Einstein deduced, that a = 1/gamma. (2) there's that point in the derivation where you plug the interim eqn for time Tau (T) into X = cT. However, what speed-of-light to use? The 1-way outbound, the 1-way inbound, or the averaged 2-way speed-of-light? I had cout = c/(2e) and cback = c/(2(1-e)), and c (=cround_trip) being the averaged 2-way light speed (invariant c). When I got to that part, X = cT, I derived the x->X transform for all 3 light speeds options (cout = c/(2e) and cback = c/(2(1-e)) and cRoundTrip=c). Not sure if any of those are definitively proper, but in doing so I found "the results did in fact support what you've stated prior in this thread", given I understood you correctly ... The LT solns "for a clock that intersects you at some point", are the very same as per SR. So in relation to the OP's Time Handoff scenario, observer A obtains the same transform solns for the B POV (who passed him by prior), no matter if SR's LTs are used, or these modified transforms are used. For any clock that does NOT intersect you, such as a clock comoving with B (that's separated from B) never intersects A, the transform solns then DIFFER from SR for that clock. The transforms are ugly, compared to the nicely reduced LTs of SR. And I mean, ugly. Here's the transforms I got ... As derived from the 3 TAUs Eqn in OEMB Section 3, but where 0 < e < 1 ... ... e(T0 + T2 ) = T1 ... e [ T0(0,0,0,t0) + T2 { (0,0,0,t0 + x’/(cout-v)+x’/(cback+v) } ] = T1[ x’,0,0,t0 + x’/(cout-v) ] The transforms attained were ... ... (Eqn 3) ... X = c[ ( (1/(cout -v) - m )/ (γn) ) (x-vt) ] ........... ← for the leading c, I used each of ... cRoundTrip=c ...... cout = c/(2e) ...... cback = c/(2(1-e)) ... (Eqn 4) ... T = [ ( n + mv) t - mx ] / (γn) where … ... 0 < e < 1 ... cout = c/(2e) ... cback = c/(2(1-e)) ... m = [ (1-e)cback - ecout + v ] ... n = (de -v2) ... de = (cout*cback) + (cout-cback)v ... γ = 1/√(1-v2/c2) Thanx, Celeritas

Temporarily under reconstrunction Thanx, Celeritas

Sorry, the EDIT feature locked me out before I could make this EDIT ... In my prior, under my response to the 2nd quote (last sentence), when I stated the above I meant this ... What I want to do next, given the derivation whereby 1-way = 2-way and e <> 0.5, is verify that per A's POV ... that Eqn 1 solns match SR prediction for intersecting clocks NOT on the A or B worldlines. I'm assuming they will. Whereby Eqn 1 was ... .... ((Eqn 1) ... t' = γ[ (1/γ2 - (2ec-v-c)v)t - (v+(1-2e)c)x)/c2 ] Best regards, Celeritas

Well, they are events. I wouldn't say it's easier, but rather that clocks intersecting are a best confirmation of the LT solns, because those clock carriers can tell everyone what their own clocks read on flyby. Of course, the eventual receipt of light signals are a confirmation of the LT prediction as well, if the owners of intersecting clocks refuse to tell us . Events in spacetime are what relativity is all about. Two postulates, a few assumptions, and events. The train arrives at the station when the small hand points to 7 and the little hand to 12. But no better event though than 2 clocks at flyby, because their readouts are then absolute. It does verify the prediction of the LTs. My derivation of the LTs for a non-midpoint reflection event (but with 1-way = 2-way speed-of-light), resulted in this generalized transform eqns (for variable time sync convention) ... .... ((Eqn 1) ... t' = γ[ (1/γ2 - (2ec-v-c)v)t - (v+(1-2e)c)x)/c2 ] .... ((Eqn 2) ... x' = 2e(γ)(x-vt) whereby e defines where the reflection event occurs in the transceiver/reflector frame ... ie reflection at t'1 = e( t'0+t'2 ) where e is in the range of ... 0 > e < 1. So for e = 0.5 (the SR convention), Eqn 1 reduces to SR's transforms t' = γ( t - vx/c2 ) and x' = γ(x-vt) as follows ... .... ((Eqn 1) ... t' = γ[ (1/γ2 - (2ec-v-c)v)t - (v+(1-2e)c)x)/c2 ] .... (............ ... t' = γ[ (1/γ2 - (2½c-v-c)v)t - (v+(1-2½)c)x)/c2 ] .... (............ ... t' = γ[ (1/γ2 - (c-v-c)v)t - (v+(1-1)c)x)/c2 ] .... (............ ... t' = γ[ (1/γ2 + v2)t - vx/c2 )] whereby the terms (1/γ2 + v2) in the time transform always equals unity. So for SR's e = ½ ... then Eqn 1 reduces to SR's ... .... (................ t' = γ[ t - vx/c2 ] However ... for e <> 0.5, then the Eqn 1 solns say this ... Wrt the time handoff scenario (for easy reference), if the A observer runs Eqn 1 for the outbound B clock, it produces the same time solns (as SR) for the B clock readout anywhere on B's own worldline. However, for spacetime events NOT on the B worldline, the time soln differs from that of SR. However since the 1-way = 2-way speed of light, all it really means is this. The transforms for events "upon" the A and B worldlines, are as per SR. Event's off the worldlines, do not match SR. But since the 1-way = 2-way is maintained "while changing the reflection event" (e <> 0.5), all this really means is this ... Whereby SR says the reflector's clock should be set to t'1 = ½( t'0+t'2 ) upon photon reflection eg say 3y-X (X is a clock at rest with A where B turns around), it may be instead set to (say) 3.8y-X per the value of e selected (where e<> 0.5). Nothing else changes, so it's just a clock set to a different time readout than SR would. The relative velocity, relative rate of tick, and geometry of worldlines remain the very same. So it's just a clock that is set to a different readout than SR would dictate, nothing more, nothing less. It's NOT as though the 1-way light speeds were altered (wrt SR) to match the non-midpoint reflection event. That's what I want to derive next. What I want to do next, is verify (per A's POV) that ... intersecting clocks are predicted as per SR, given neither of those clock's worldlines are the A or B worldlines. I'm assuming they will. Well, I'm in the process of deriving the transforms for 1-way <> 2-way, as a function of the selected e, although I must say it's somewhat a mess because nothing reduces much. I'm not going to concern myself with the reductions though, I'm only interested in making the required substitutions as in OEMB. That's all you should need. A spreadsheet can handle anything you throw at it, ugly or not, assuming it's (of course) correct. So, I'll keep plugging along here, although I'm not moving fast because of other life related matters. I'll let you know what it reveals md. And, thank you for your time on this. Much appreciated. Best regards, Celeritas

md65536 and studioT, First, I reread one of md's prior post. I should say that while I've been thinking in terms of 2 differing alternate theories (SR is 1 of them), I see now that md35536 has been responding strictly about 2 competing versions of SR (so with different conventions of simultaneity). However, I'd been assuming that a 1-way <> 2-way speed-of-light would produce LT solns that differ from SR (but I keep the 2-way = c). While I realize that coordinate time differentials diminish (between the 2 versions) for a moving clock that approaches intersection with my clock, and vanishes upon intersection (coordinate time becomes proper time), I was not sure that the intersection of remotely located clocks would be as such. The more I think about it though, and after rereading what you've posted, the more it seems it would be as such. In which case, the geometry of the worldlines is identical to SR's version, the time readout of the clocks are the same for all points on their worldline, and the change in time sync convention would have no impact on the time readout of intersecting clocks anywhere in spacetime (same as SR). If that's what you've been saying, and all that is true, then both versions produce the exact same results, even though the predicted coordinate (not proper) values differ (wrt SR). Before I go further, please let me know if I'm on track with your reasoning, or not. Thanx. PS ... StudioT brought up the inertial AB scenario. Two clocks A & B happen to read zero at their flyby. The question was ... Which clock ages 4 years first? Not sure why you bring up this scenario, as it's standard SR. The clock that ages 4y first (since flyby) depends on who you ask. Each clock will (of course) claim itself to age 4y first, and the moving clock to age 4y later, because of the Relativity of Simultaneity. I just was not certain what the precise impacts would be if the SR convention were changed, ie what all must change with a non-midpoint reflection event in Einstein's emitter/reflector frame, and how the transform solns might be impacted (if at all). It's one thing to imagine a reslanting of lines-of-simultaneity on a spacetime diagram, but is that precisely what a rederivation of the transforms (from scratch) would actually produce for a non-midpoint reflection event and 1-way <> 2-way? I wasn't quite certain. I'm now thinking it would produce the same. I gotta say tho, the transforms are very ugly when the 1-way <> 2-way (with 2-way = c). Nothing during derivation reduces much. Thanx Celeritas

md65536, Wrt my prior post here ... on the other hand, if the coordinate time were to differ in that way (for example, say) 5.2y-B and 5.2y-C at their flyby event, whereas SR says 4y-B and 4y-C, then I would venture that a moving clock's tick rate would have to differ somewhat from what SR predicts. If so, then I see what you were saying prior, about ... "what are the specific things envisioned to vary" in an alternate theory (compared to SR). Wrt what I had been working on ... I've been trying to derive the LTs (in the OEMB way, but) for a non-midpoint reflection event. When I did that, it did not change any spacetime transformation solns, but I had kept Einstein's convention of 1-way = 2-way speed of light. So I've redefined the 1-way outbound light speed and 1-way inbound lightspeed to be consistent with the non-midpoint reflection event. Only problem is, the derivation gets very messy fast, as they do not reduce elogantly as in OEMB. It's pretty ugly, and Occam certainly would not favor it, but that's fine as a spreedsheet can handle it, elogant or not. I'm not assuming a master frame either. I'm assuming all frames use the same such convention. Anyway, I was just curious what the solns would be, and as to how they would differ from SRs. I was mainly interested in the coordinate solns and how they differ from SR, but really, it's about "the all of it". Best regards, Celeritas

From A's POV at 5y-A, he runs the LTs to predict that the B & C clocks now read 4y-B and 4y-C at their flyby, way down yonder 3 ly distant. Those are coordinate times as calculated by A using the LTs. A is "not there", and the B/C flyby event does not occur on the A worldline. On the other hand, if you ask B what his own clock reads at B/C flyby, he'll say 4y-B which is a proper time for he himself, because the flyby event occurs at B on the B worldline. If you ask C what his clock reads at B/C flyby, he'll say 4y-C, which is a proper time for he himself, because the flyby event occurs at C on the C worldline. I've brought up this point a ways back ... that a coordinate time of a remote moving clock (per one observer) is the proper time of that clock when it displays that time (per he who carries that clock). So the point I've been making thus far, is this ... any alternate theory that produces coordinate times that differ from SR, should not be able to predict B & C to execute a flyby at 4y-B and 4y-C. If it produces different coordinate times wrt SR, I'd expect such a theory to predict (for example, say) 5.2y-B and 5.2y-C at their flyby event. The B & C clocks will verify they read some specific values at their flyby event, and only the theory that predicts that, wins. Of course, we won't be running such a flyby test anytime soon. Best regards, Celeritas

Sorry md, but I'm not quite following your responses here. For example, I'm talking about a deviation from SR whereby the 1-way <> 2-way speed of light (not Lorentz's theory tho), but you have responded with things like "there's no difference between polar coordinates and catesian coordinates. Well, of course there ain't, but I don't see how that relates to what I've been asking about ... When it comes to 2 theories eg 1-way=2-way (SR) versus 1-way<>2-way (again, not talking Lorentz's theory), I just don't see how that relates to "choice of differing types of coordinate systems for a single theory (eg polar vs cartesian)? I've been assuming the same coordinate system is used by alternate competing theories (eg Cartesian alone). If all you are saying is that "for differing theories, given they produce the same time readouts for any 2 intersecting clocks in space and time, then they are valid theories", then I'm in agreement with that. Einstein's and Lorentz's theories are 2 such theories, although only one theory (eg as SR) may be preferred for various reasons. And, of course ... the OP says 4y-B and 4y-C at their flyby event per scenario setup, per SR. However ... You say that the time readout (now) on the A-clock is a coordinate time per B & C at their flyby event, because A is remotely located wrt them. I said that the time (now) on the B & C clocks at their flyby event is also a coordinate time per A, because B & C are remotely located wrt him. If 2 competing theories produce different coordinate times, then how could both those theories allow A to predict the B & C clocks to read 4y-B and 4y-C per A at the B/C flyby event? It just seems to me that if both theories predict the correct time readout on 2 clocks during their remote flyby event, which can be anywhere in space and time, then I don't see how they can disagree on the coordinate time of remotely located moving clocks. SR, I understand. Differing coordinate systems I understand, eg polar vs cartesian. I'm just trying to grasp the impact of deviations from SR, particularly in relation to time-sync-convention and the 1-way speed of light (<- not Lorentz's theory tho). Thanx for your time md. I'll just try to complete my LT derivation of a variable reflection event, so t'1 = e(t'0+t'2) , so not just the case (eg per SR) where e = ½ which requires the 1-way = 2-way. All I was aiming to verify is whether such a theory would produce different coordinate times for remotely located clocks, and whether such a theory would differ from SR in the time readout of 2 clocks executing a remote flyby event ... eg the current time readout (per A) of the B & C clocks 3 ly downrange at their own flyby event. Thanx, Celeritas

md65536, I realize that coordinate types are a choice, and that events in spacetime are what's true or real. However, there's one particular point that I need to clear up. I've asked before, and I may have misunderstood your response in regards to this. You've said that alternative theories can produce different coordinate values for remotely located moving clocks, yet still be right. Consider these ... Per SR, per our Time Handoff scenario, the A observer predicts the B clock to read 4y-B, and the C clock to read 4y-C, upon B/C flyby. So ... (1) In an alternate theory, A predicts the B clock to read 4y-B, and the C clock to read 6y-C, upon B/C flyby. How can it be said that both theories are correct? Or ... (2) In an alternate theory, A predicts the B clock to read 6y-B, and the C clock to read 6y-C, upon B/C flyby. How can it be said that both theories are correct? When 2 clocks execute a flyby event, they have a specific time readout when they do, and all in the cosmos must agree. Only the theory that predicts the correct readouts, is a valid theory. If 2 theories can disagree on coordinate time solns for remotely located moving clocks, how can those 2 theories agree on the coordinate time (current time-readout) of intersecting clocks at their flyby event? Said another way ... if the time readout of 2 distant intersecting clocks read 4y-B and 4y-C at their flyby event, those times being coordinate-times of B & C per A, how can a (assumed) valid theory "that produces differing coordinate times (wrt SR)" predict their flyby "at the same readouts of 4y-B and 4y-C"? Thanx, Celeritas

md65536, Thanx for the response. I understand what you're saying there. There are various ways of considering theories different from Einstein's. There's Lorentz's version, which uses a master frame while using the Einstein/Poincare convention for simultaneity. The transformation solns are the same as Einstein's because obervers moving thru the preferred ether frame use length-contracted rulers to measure equally contracted-lengths, and similary for using time-retarded clocks and while measuring dilated durations. Also, while all observers of a single frame use the Poinare/Einstein clock sync procedure, those co-moving thru the ether believe they are synchronised while in reality they are not (but don't know, and cannot tell). Here, while simultaneity differs wrt SR, the LT solns are all the very same. I'm wondering whether Lorentz could even have developed his theory, had light been used as the definition for the metre in 1905? I suppose it could, since all observers measure its speed the same anyway. Your example uses the sort of preferred-frame theory that differs from Lorentz's, using slightly different assumptions, principles, and/or postulates. Such as, light speed is invariant in only the preferred frame, but is measured variantly by observers moving wrt the preferred frame (different from Lorentz's). I see your point, in that the transformations of space & time (of course) depend on the apriori assumptions, principles, and postulates used. If various theories can produce self-consistent space & time solns, based upon each their own (reasonable) apriori assumptions, principles, and postulates, then how to say the theory is wrong even if it produces space & time solns that differ from SR? All the tests of relativity to date support Einstein's version, and Lorentz's. Einstein's is preferred for various reasons, eg no ad hoc explanations are required, it's mathematically self consistent from 1st prinicples, it allowed for the general theory of gravity, and Occam's Razor supports it. I'm supposing that all the (non-Lorentz) preferred frame theories of the prior para here, have been proven false by all the tests fo Relativity to date. Yes? So out of interest, I re-derived the LTs (as per OEMB's) using a non-midpoint reflection event, whereby I defined the reflection event as a variable (e) whereby 0 > e < 1. Einstein's convention would use ½, so only e = 0.5. It turned out that no matter what "e" I select, the spreadsheet produces the very same LT results as SR, but that's only because I hadn't yet completed it ... whereby the outbound 1-way light speed must differ from the inbound 1-way light speed, given the reflection event does not occur at half the roundtrip durarion. Of course, the 2-way speed of light remains at c. So, that's next. However, I was not assuming a preferred frame, but rather whereby all observers use the very same convention and assumed equally correct (which I'm not sure even makes sense yet?). So, I'm not really sure yet if it's even worth the persuit. And, how to define the meter's length, if light speed outbound differ's from light speed inbound? It seems you could not use light's wavelength for defining the duration of the second or the length of a meter. Yes? Best regards Celeritas

md65536, OK, so correct me if I'm wrong, but wrt your understanding of time sync conventions ... Given a remotely located moving clock at an event, if the 1-way and 2-way speed-of-light is not equal, then coordinate time solns will differ from SR. Also, the relative rate of a moving clock would not differ from SR (it's the same), given the same worldlines geometry. Is that the way you see it? I was wondering whether the relative rate of moving clocks would differ (wrt SR) with 1-way <> 2-way, or not. Thanx, Celeritas

Just FYI, the spacetime diagram, and geometry of worldlines ... Best regards, Celeritas

That sounds good to me. The OP had no acceleration by definition. OK md65536, wrt your pouring water into heated kettle analogy ... The act of pouring the water, is akin to the act of the twin B starship being transported to the earth launchpad. Applying a flame to the kettle to raise the water temperature, is akin to burning the rocket thrusters (proper acceleration) to raise the starship velocity (frame transitioning). Stabilizing at 212 deg F (boiling), is ~akin to coasting at speed inertially (no thruster burn, no acceleration). The water boils because the water temperature reached 212F. It reached 212F because the flame was applied. OK, so let us imagine a kettle of cold water sitting on an un-lit burner. Next, the professor says ... please boil the water. Do we just wish the 212F into existence, or do we apply the required flame? Bottom line, if twin B does not undergo proper accelerations, he can never age less than twin A (per the stated scenario). I agree with the highlight above. (EDIT addition: Twin B is colocated and comoving wrt twin A at the getgo. For twin B to age less than A, in an absolute manner where all in the cosmos agree, he simply must change his worldline orientation to do so. That is, he must make TURNs in 4d spacetime, ie transition fames of reference. In flat spacetime, that requires twin B to undergo proper accelerations. B must later re-unite with A. B's proper saccelerations produce all the velocities that create the required geometry of worldlines, and their length which is the accrued proper time). Anyways, I fully agree that the relative aging between the twins is determinable from the accrual of proper time alone. And since by definition no time expires during periods of proper acceleration, the relative aging is determined strictly by the inertial phases of flight. This is nothing new. All inertial scenarios possess relative time, and so relative aging is inherent there as well, although its relative per POV. The OP has all that, as it's an all inertial scenario. It's always the accrual of proper time that produces the worldline length, and/or vice versa. What the OP does, which sums the proper time of 2 different POVs, is to show that the relative aging is the result of the worldline geometry. One more ... I should say, I do like your posts md65536. Very informative, always very well stated, and enjoyable. Best regards, Celeritas

OK, thanks md. Long ago, I tried deriving LTs using a non-midpoint reflection event in the k system. I remember the derivation got rather ugly, fast. It did not simplify very well at all. Yes, that's the conclusion I came to, way back. I was second guessing that last night, as it had been awhile. I may have to try that derivation again, although I presume it's likely been long on the web somewhere, so maybe I'll look for that. Wrt 1st highlight ... Yes, the coordinate time of a remotely located moving clock was the focus of my question there. Wrt 2nd highlight ... One can envision virtual clocks everywhere and anywhere in spacetime. Any virtual clock should be substitutable by a real clock. I would imagine this true no matter if 1-way = 2-way or not. You said above that for 1-way <> 2-way, coordinate time calculations for remotely located clocks would differ from SR solns (using 1-way = 2-way), except where 2 clocks intersect. However no matter the convention, we can still envision virtual clocks everywhere and anywhere in spacetime, including virtual clocks intersecting at any and all points in spacetime. Virtual clocks should always be substitutable by real clocks. So it seems that even for intersecting clocks, if 1-way <> 2-way then the spacetime solns should differ from SR's solns. No? I see, that's fine Markus. Thanx. I realize that everyone agrees on the twins solns, and why it happens. My discussion with md65536 was focused strictly on whether one can say "acceleration does not cause the twin's relative aging differential". Md65536 associates "felt force" with proper acceleration. If twin B has thrusters on opposite sides of himself, and they fired equally, he feels his compression but goes nowhere. Also, that the huge inertia felt by B at his own (virtually) instant turnabout can play (virtually) no role in the relative aging outcome, because (virtually) no proper time is accrued during that period. However, it's not really about the force felt during B's proper acceleration, it's about "the transitioning of inertial frames of reference", which requires a proper acceleration by B in this twins scenario. This is just to say that twin B's proper accelerations are required to attain the worldline geometry that produces the result of twin B aging 8y to twin A aging 10y. I think this famous debate is the result of the scope in which one considers the question ... ... (1) Highest level consideration ... use the geometry of the A & B worldlines. ... (2) Easiest restricted consideration ... use the accrual of proper time alone, for both A & B. ... (3) Hardest restricted consideration ... use the accrual of proper time for A (or B), and the accrual of coordinate time for the other observer B (or A). All 3 work in so far as calculating the round trip relative-aging. And of coures, for otherwise SR would be an incomplete theory. Regarding (2) vs (3), using (3) requires the consideration of the twin B transitioning of frames, from his own POV. It is there that the role of frame-transitioning is revealed, because one must then consider the more difficult aspect of a dynamic change in twin B's sense-of-simultaneity at turnabout per himself. My point is that while proper time is all you need, it's the frame transitioning that attains the required geometry of worldlines to produce 8y-B to 10y-A. That said, while all 3 work, (1) presents everything in a nutshell. A picture paints a 1000 words. I'll have to address md65526's anaolgy wrt boiling water next, see where it all goes. Best regards Celeritas