Maximillian

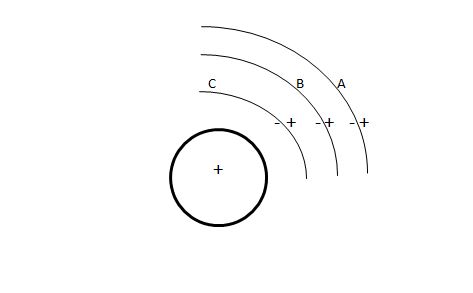
Enclose a positively charged sphere in neutral concentric spheres as shown in the image. Connect outer surface A to Earth, inner A to outer B, inner B to outer C and finally inner C to the central sphere. These spheres are good electric conductors and are insulated from one another. When you discharge a charged body using the laws of conservation of energy the electric energy of the current that flows is equal to the energy you put in charging the body, the description shows that on top of Earthing the system we can still get more electric energy flowing in different parts of the system due to the presence of the same charge. So little electric potential energy in the central sphere say 10J is giving rise to say 100J electric energy flow. Will I get more electric energy flowing than the electrostatic potential energy stored in the central Sphere?

The system works and I have scientifically proven that. Whether you accept it or not it speaks for itself. I have to admit that your responses have helped to prove that it actually works.

Finally my equations have been approved to be correct https://answers.yahoo.com/question/index?qid=20160914073523AAhRFp3. In this case g was 9.8ms-2 therefore the energy was 19.6J input which makes the ball less dense and by all means gets to the water surface gaining a gravitational potential energy of 100J. You say am starting from a charged battery true but if that charged battery has 20J of electrical energy it will never output more than 20J of whatever kind of energy. You don't need a closed cycle to prove the conservation of energy, so what happens if that cycle is never closed does it mean energy conservation will be violated. What you need is to measure the total energy of an isolated system now then measure it in the future, it should be the same. What is for sure is we input 20J of pressure energy and we have outputted 100J of gravitational potential energy. To conserve energy the water has to provide the extra 80J but its definitely not from us.

I used 20J of pressure energy to make a magnet in water gain 100J of gravitational potential energy on reaching the water surface. It starts falling down with a kinetic energy of 100J through a wire coil, by the time it has landed down it has produced for me electrical energy of 100J that I store in batteries. I threw the ball up with 20J of energy but I now have 100J of electricity stored in my batteries. Have I not gone through a complete cycle and still have more energy?

Yes, in a closed loop I have expended 20J to gain Zero energy. Imagine the fish gets to the top using 20J instead of 100J and never returns, what happens to the conservation of energy?

Please can you help me with the answer am trying to compare it to mine. Zero displacement obviously means no energy can be extracted. Imagine am a fish all I want is to use little energy to enable me reach the top of the water. I use 20J which should put me 2m above the water bottom but it takes me 10m at the surface.

How much Energy do We need to increase the volume of a ball by 0.0002m3 at constant mass at 10m below the water surface?

Please can someone use available equations to prove the paper wrong especially the energy needed to give the ball for it to rise to the water surface? What will stop it from rising to 10m with a density less than that of the air assuming the atmosphere has a height of 10m or what will stop the ball rising to the top of the water when its density is less than that of the water?

That's what exactly is beating my understanding.

This is getting harder to explain than I thought but I will try to be clear as possible. If this can work in water it means it works in air. Now imagine the ball is lying on the Earth's surface I give it a pressure potential energy of 20J and it rises to a gravitational potential energy of 100J. With the energy I input I expected it to rise to a height not more than 2m but it reaches 10m above the Earth. Isn't that violating energy conservation?

I can see we are coming to a conclusion. Its obvious that when the ball returns to the surface it has covered a zero displacement, and from energy is equal to force times displacement you get zero energy with zero displacement. That's elementary physics. What your not understanding is giving a body 20J and it rises to a height that has an energy more than I input. To put it in simple words is imagine I kick a ball with 20J I will expect it to rise to a maximum height equal to 20J but weirdly it reaches the mountain top equal to 100J.

Then when it gets to the top what is its gravitational potential energy? Yes you get the 100J back but how much energy did you input to acquire the 100J at the rise? And its for that reason that I asked the question in the first place. How much energy did I input to the ball to get 100J gravitational potential energy?

Correct, I added 20J of gravitational potential energy to the water by expanding the ball. From your example this gives the water 110J which is enough energy to help the ball attain 100J. I can see you are also coming to the conclusion that we input only 20J but have got out 100J.

What makes you think it was rejected when you can't disapprove it? Lets start at the top of the tank. In this case we don't need to carry it up since the ball is at the same level with the water surface so no -100J needed. So we started from the water surface, sunk the ball and it rose back to the water surface. 0-20+100 = 80J which is created energy. Even if it didn't work the question would be are our equations sufficient? Since theoretically it seems to work but practically it doesn't. Anyway try it out practically for yourself you will be amazed.

I don't have to always carry it up, lets assume its a river or lake at sea level we shall not need the -100J. 0-20+100 = 80J which is created energy. For the tank of water at 10m up, Lets say the densities I have stated are composite. Combining a pocket of air and some dense material. In the first instance when the ball sinks the air pocket is at atmospheric pressure. I then reduce that density to let the ball float. At the top I unlock the structure holding the air pocket so that the atmospheric pressure pushes it back to its original volume without me using any energy which makes it more dense hence it sinks. You now see that I can perform this repeatedly. So you will get -100+0-20+100+0-20+100 = 60J of energy have been created in just two sinks. The more you repeat the process you will create more and more energy. So are you saying bodies never posses gravitational potential energy?