Vay

Force is in newtons and mass is in kilograms. The units shouldn't be important to the question; it's more of a conceptual problem. Why do we use tension instead of the force of the blocks. I thought if someone was pulling a cord attached to a pulley, the tangential force would be the force of the hand pulling it, right? But the book says it's the tension force. It also turns out the tension forces calculated for the two mass-less cords are not the same as the force of the two blocks. The book doesn't mention the mass of the pulley, that might be why, but I am still trying to figure out the link. The way I see it is, the difference between the forces acting on the block, is the same amount of force lost in turning the pulley. This force difference between the two blocks gives the pulley the turn, and is the tangential force on the pulley, am I right? Edit: My prediction is wrong since Mass(2) and Mass(1) both have the same same magnitude of acceleration, but in different directions, so that means their forces are already different before losing some force into turning the pulley. I think I solved the problem: The force acting on the block is not the same as the tension force. This is because the block is left to freely fall, meaning the force on the block is greater than the tension force. If the tension force was (Mass(2))(a), then the Mass(2) would not be falling. Force Mass(2)(a) is decreased from Mass(2)(g) because of the inertia of the pulley and the inertia of Mass(1). This reduction of force means that there is a force pulling in the opposite direction of Mass(2), which is the upward force of Mass(2)(g)-Mass(2)(a). Given that Mass(2)(a) > Mass(2)(g)-Mass(2)(a) because the upward force on Mass(2) does not stop Mass(2) from falling, means that the tension in the cord is Mass(2)(g)-Mass(2)(a), and since the cord is in contact with the pulley, the tangential force is the tension force, which is Mass(2)(g)-Mass(2)(a). Without the tension force, Mass(2) will fall freely. TLDR: The pulley is not actually supporting a force of Mass(2)(a), because if that was so Mass(2) would not be falling. Instead, the pulley is supporting, with the help of Mass(1) weighing in on the other cord, a different force, a smaller force, which is the tension force in the cord. This concept is still not crystal clear in my mind and so I will probably forget it during the finals...

A pulley is attached to the ceiling. Two masses hang from the pulley, one on either side. Mass(1) is smaller than mass(2), all in terms of kg(kilograms). We take downward as positive direction. The cords attaching the masses are mass-less and does not slip on the pulley. The question is to find the tangential force on the pulley. The book says the net tangential force on the pulley is (tension(2) - Tension(1)), where the unit of force is N(newtons). I thought the net tangential force acting on the pulley is (Mass(2))(a)-(Mass(1))(a). Anyone know why I am wrong?

Isn't the intergral of (cos(x))^2, from 0 to 2pi, equal to pi/2? Or are you taking the integral of something else. The graphical interpretation makes more sense, where we're just taking the average of the two extreme y values of (cos(x))^2.

In reference to the average change in kinetic energy over time for waves moving along a string, (1/2)*u*v*(w^2)*(ymax^2)(average of ((cos(kx-wt))^2) over time), my textbook says "the average value of the square of a cosine function over an integer number of periods is (1/2)", thus the above equation reduces to (1/4)*u*v*(w^2)*(ymax^2). Can anyone explain the cosine identity, or whatever it is, used here(the other variables are not important, I only have question about the identity in the quotations)? Also, what is the difference between the speed of waves defined as v = (wavelength)*(frequency) and v= square root of (tension/linear density)? My book says the speed is related to wavelength and frequency, but it is set by properties of the medium, which is the tension and linear density. Can someone explain this clearer?

Perhaps a better question is, In the case of looking downward on a disk rotating clockwise, what exactly is moving downward when right-hand rule is applied? I can learn to calculate it in vector notation, but I can never understand why it is calculated the way it does in three dimensional analysis.

So, the right hand rule is established purely for communication purposes; to tell the point of reference of the original observer?

When a car drives in a circular motion around a center of reference, friction exists between the tire of the car and the road such that the car accelerates toward the center of circular motion. On a flat plane, friction is enough to contribute to centripetal force or acceleration. In a banked situation, ignoring friction, gravity contributes to the horizontal component of normal force which affects the centripetal force on the car. The normal force is caused by the weight of the car, or gravity. Normal force is perpendicular to the plane of inclined bank surface. Because inclined normal force has a inward, horizontal component, then an inclined plane in the absence of friction, is enough to provide centripetal acceleration and force. In the case of banking, depending on the direction of banking, gravity contributes in different ways. If the banking is inward, as in a 'U' toward the center, then gravity pulls down on the car, conversely the opposite when it banks in an 'n' because gravity would be pulling the car away from the center of circular motion(not centripetal). If the road is banked inward, ignoring friction, then the tilt of the bank by itself is sufficient enough to give a car driving around the banked plane a centripetal acceleration and force. Then centripetal force is -(normal force)*sin(theta) = -(centripetal force) = m((-(v^2)/R). -(normal force)*sin(theta) finds the inward horizontal component of the normal force. Since the equation uses normal force, that means you must take into account the effect of gravity on the car. If friction exists, you must find the horizontal component of kinetic friction parallel to the horizontal component of normal force on the banked road in order to find net centripetal acceleration and force inward. In conclusion, the banking incline of a plane and kinetic friction both contribute to centripetal acceleration and force of a car driving around the fore-mentioned incline plane. Both scenarios use the normal force, thus factoring in effects of gravity. ((Kinetic friction) = (coefficient of kinetic friction) * (normal force))

For example, in an angular rotation, the direction of the velocity of angular rotation can be found using the right hand rule. A disk rotating clockwise has angular velocity downward on the rotational axis. Now, I want to ask, what does it mean by the angular velocity is downward? Isn't the angular velocity in the clockwise direction, so where does this downward direction come from? (Don't say, "it's because of right hand rule", because that's just begging the question).

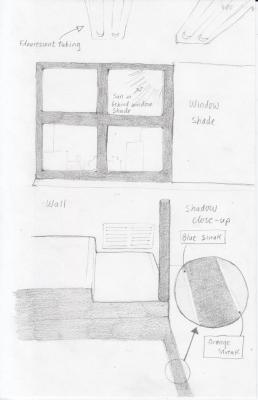
I have attached a sketch of the scene I remembered, so it is not an 100% accurate representation. The circle on the right is a close-up of the shadow of the pipe. I can't get a picture because I am on spring break. The blue and orange streaks are brighter than the surrounding light when the streaks are concentrated onto a thinner line, which makes sense. At different shadow angles, the streaks disperse and are not as bright anymore. The fluorescent bulbs on the ceiling are on.

I saw it in class, plus I don't have a USB for my flip-phone to transfer pictures, but I will draw it and label it, then upload it here.

Thanks I am not up to that in my physics class yet, still doing mechanical motions. But I will definitely refer back to this problem after I do study it. The resources online doesn't really help too much, they go into the equations and what-not. Although I realized that my diffraction scenario would be just a pipe blocking the sunlight, such that the light will shine completely on both sides of the pipe. I have no clue what such diffraction pattern would look like. I also forgot to add that the room I was in had fluorescent bulbs on, so that might add some implications.

The sun shines through the window and casts a shadow of a black pipe vertically onto the ground. The resulting shadow has different colors on different sides. Relative to the sun on the left side, the edge is orange-ish in color, and the right edge is blue-ish in color. At certain places, the edges have no orange-ish nor blue-ish colorations, particularly the part of the shadow closer to me. Furthermore, at different angles of shadow cast from the sun, the colored edges changes in sharpness, going from blurry to a sharp "clean" that seems even brighter than the actual, adjacent light on the ground. I might have an idea why the edges change in sharpness, but I am completely oblivious to why the edges are different colored. Any the answer?

The work done by a variable force with respect to x distance is the integral of the function of that force with respect to x distance. But say we have a variable force as a function of time, can we say that the integral of the force with respect to time is equal to the work done by that variable force as a function of time? Also, if I have the acceleration of a particle as a function of term and I have the mass of that particle, can I multiply the mass and acceleration to find a variable force as a function of time? My intuition says yes to both question, but calculating the work using distance gives different results from calculating work using time.

Thanks, I get it now. I just referenced back to the power series and found that it was just its formulation. Another thing has troubled me, it's the 'a' of the Taylor series. Can it be anything? It seems the book is taking random values. Does it mean we can pick any value of 'a', or is there a set center 'a' for which a series would work? It doesn't make a lot of sense to me that there is always a center for the intervals of convergence, and that we can pick this center anywere, at least for the series that converges.

When you find the Maclaurin series form of f(x)= e^(-3x), you will get the summation from n=0 to infinity of (-1)^n * ((3^n)/n!) * x^n. The question is, what is the reason for assuming that the X factor is always x^n, how do we know its not x^(2n) or x^(3n)?