

JVNY
-
Posts
52 -
Joined
-
Last visited
Content Type
Profiles
Forums
Events
Posts posted by JVNY
-
-
. . . Considering from the lab (center of ring) frame, it must be that all of the ring clocks tick at the same (slowed) rate. . .
From the perspective of a ring observer, the clocks on the ring cannot be synchronized. A single pulse from the center will reach different clocks at different times. Yet the ring clocks must all tick at the same rate, so there must be a "shift" in simultaneity, where --- I think --- the clocks in front of an observer (with respect to the ring's rotation in the lab frame) are behind in time, and ones behind are ahead in time. (Is this right???) At some point near halfway around the ring, one of the clocks can be in sync with the observer's. . .
A couple of thoughts.
First, I think that even on the rim (not just in the lab) each clock will tick at the same rate. Say the interior of the rim is mirrored, so that a light signal can travel around the interior. If a clock sends a series of signals around the ring (in either direction), one every second of its proper time, then each other clock on the rim should receive the signals one every second of its proper time (after the initial delay for the first signal of the series to arrive).
Second, you are on to something with the simultaneity shift suggestion -- some analyze the Sagnac effect as a shift in simultaneity, like this: http://www.physicsinsights.org/sagnac_1.html
However, I don't think that the shift in simultaneity view follows the c+v and c-v analysis of how light travels on the rim (to a rim observer), because the Sagnac effect is the same in absolute value for both the counter- and co-rotating signal (plus or minus 207.4 ns for a signal sent around the earth per the Ashby article linked above). It is definitely worth thinking through.
0 -
I am trying to get at the point of view of the rim, not the axis. If a rim is rotating in an inertial laboratory, it makes sense that signals sent in opposite directions around the rim travel in the lab frame relative to their starting point on the rim at c+v or c-v. However, the result of +v or -v applying is that the difference in lab time between the arrival of counter- and co-rotating signals back at their starting point on the rim will depend on the speed of the signals.
On the rim, however, the difference in arrival times does not depend on the speed of the signals. Any pair of opposite signals sent around the rim (light flashes, slow traveling portable clocks, etc.) will have the same difference in arrival time due to the Sagnac effect as measured by an observer fixed on the rotating rim. See, for example, Ashby and Allan on slow clocks carried around the earth (http://tf.nist.gov/timefreq/general/pdf/133.pdf , page 652), and Ashby on clocks around the earth that are synchronized using the Einstein convention with light signals sent around the earth (http://areeweb.polito.it/ricerca/relgrav/solciclos/ashby_d.pdf , page 15) (excerpts attached).
Because the difference in arrival time as measured on the rim (by an emitter and receptor fixed on the rim) does not depend on signal velocity, it cannot be right to explain the Sagnac effect as being due to light traveling at c+v or c-v as measured by a rim observer.
The standard explanation seems to confuse what is happening in the inertial laboratory frame with what is happening on the rim itself.
0 -
I don't know anything about the Sagnac explanation.
Variables v and c are speeds, not velocities; there is no object in the rotating ring that has a constant velocity. Could you treat the ring as a set of individual objects, and compare the speed of light to the nearest object, considering only the object's "momentarily comoving inertial frame" (MCIF)? Could the explanation refer to each infinitesimal section of the ring as the "some other object"? Each section of the ring would have its own MCIF, but since they're all the same except for their direction, if you're only dealing with speed and ignore direction, you can deal with all the sections as if they're the same (object).
I suspect that you can do this. You might not even need more than one section. Say that you have (1) a stationary, hollow cylinder with its inside surface mirrored, and (2) a single light emitter/light receiver unit. You set the unit into motion circling around the interior of the cylinder like a motorcycle in the classic "wall of death" carnival sideshow, see http://en.wikipedia.org/wiki/Wall_of_death_(carnival_sideshow). Then the unit sends a flash of light in each direction. I suspect that the same result would occur (the unit would record a fringe shift for the returning flashes when they arrive at the unit). Dufour and Prunier ran the Sagnac experiment with different parts of the device fixed in the lab rather than on the disk (such as fixing some of the mirrors in the lab), and their experiments got the same approximate fringe shift results as the one with all parts fixed on the disk. See http://www.conspiracyoflight.com/pdf/Dufour_and_Prunier-On_the_Fringe_Movement_Registered_on_a_Platform_in_Uniform_Motion_(1942).pdf
0 -
Makes sense, thanks.
0 -
Thanks to both swansont and phyti. The thing that confuses me about the particular quotation is the phrase "the sum and difference of the speed of light and the speed of some other object, both with respect to a single inertial coordinate system . . ." Given that the emitter and detector are both on the disk, the result (fringe shift recorded on film) has nothing to do with any inertial coordinate system.
If you set the interferometer into translational movement rather than rotation, the film will not record any fringe shift (swansont: "you get a fringe shift in a rotating Sagnac interferometer but not in a translating one"). It is only in another inertial coordinate system (say a laboratory relative to which the interferometer is moving) that one would observe light to move relative to the interferometer at c plus or minus v.
Given that the entire experiment (including the photographing of the fringe shift) occurs on the disk, which is not inertial, utilizing the concept of "a single inertial coordinate system" seems irrelevant and confusing.
0 -
Here is a typical explanation of the Sagnac effect:
Clearly the pulse traveling in the same direction as the rotation of the loop must travel a slightly greater distance than the pulse traveling in the opposite direction, due to the angular displacement of the loop during the transit. . . [T]he expressions "c+v" and "c-v" appearing in the derivation of the phase shift . . . do not refer to the speed of light, but rather to the sum and difference of the speed of light and the speed of some other object, both with respect to a single inertial coordinate system, which can be as great as 2c according to special relativity . . . http://mathpages.com/rr/s2-07/2-07.htm
I am having difficulty grasping this explanation because all parts of the interferometer in the classic Sagnac experiment are fixed on the rotating disk (including both the light source and the film that receives and records the light waves). So the experiment does not seem to measure light speed plus or minus rotational speed with respect to some inertial coordinate system (such as the lab system in which the disk rotates). The experiment seems to measure light speed entirely with respect to points on the disk.
Can anyone offer suggestions about how to interpret or supplement this explanation? Thanks.
0 -
I think that they even state that the line for the actual path is straight (no aberration) because the aberration is so small that it cannot be represented in the simple drawing.
-1 -
Taylor and Wheeler (if that is their drawing) are wrong on both accounts.
It is essentially their drawing (without copying it outright and violating any copyright they might have in it).
But remember that they expressly state that they are modeling a different path than the actual experiment, in order to simplify the math. They acknowledge that their answer is therefore only an approximation of the actual experiment. Their method yields 250 microseconds; xyzt recalls that the actual is around 200 microseconds. So it is clearly only an approximation.
-1 -
. . . Do Taylor and Wheeler use the coordinate speed of light in their calculations? Can you post them?
Sure. Although I do not understand them, I can post them for you.
For radial path segments they use:
dr/dt = 1 - (2M / r) [note that for c=1, I believe that this is the same as your post 3 formula:
 ]
]and then integrate:
dt = dr / (1 - (2M / r))
They define r as the "coordinate" radius (or reduced circumference, or r-coordinate) and say that it is called a radius "despite its being no true radius" (page 2-9).
They use an approximation for 2M/r:
(1 + d)^n = 1 + nd
And from this they get 53 microseconds delay for the radial segment Earth to Sun.
Then, for tangential semicircular path they use:
ds/dt = (1 - (2M / r))^(1/2)
They assume that r = R for the entire semicircle, so they solve that equation for dt and sum it along the entire semicircular path of length πR, being:
πR / (1 - (2M /r))^(1/2)
And they use the approximation again and get a delay of approximately 15 microseconds.
They don't do the Sun to Mars segment in detail, but they instruct the reader to use rMorbit = 2.28 E +11 meters, and they say that this generates a time delay for that segment of 57 microseconds.
So their total time delay is 53 + 15 + 57 = 125 microseconds each way, or 250 microseconds for the round trip.
The chapter on the time delay is a "project," so Taylor and Wheeler do not show each step of their calculation. They show what I posted, generally saying to the reader to use certain formulas and then ask the reader to show that the results are the numbers above.
2 -
It seems that the biggest issues are (1) whether slower coordinate speed of light has any physical meaning, (2) if one believes so whether one is mainstream or fringe, and (3) whether the coordinate speed of light (the speed as measured by a distant observer) is a valid explanation of the Shapiro delay. Taylor and Wheeler are certainly mainstream, and here are excerpts from their book "Exploring Black Holes: Introduction to General Relativity." The text answers the questions (1) yes, (2) mainstream, and (3) yes.
Project (i.e., chapter) E is titled "Light Slowed Near Sun." That pretty much answers all of the questions implicitly from the start. Here goes with excerpts. The text sets forth the initial questions:
* What happened to "Light always moves with the same speed"?
* Who says light slows down near Sun?
* How much does light slow down near Sun?
* Does observation verify the predicted value of the slow-down? [from page facing E-1]
The Schwarzschild bookkeeper records a "smaller speed of light" than do . . . free-float observers . . . That is the prediction of our analysis . . . Does this prediction have a physical meaning at all? Is there any way to measure this "slowing down of the speed of light" as reckoned by remote observers? "Yes" and "yes" were the answers predicted by Irwin Shapiro and demonstrated by him and coworkers. [from page E-1]
So, Taylor and Wheeler literally ask the question whether the slower speed of light as reckoned by remote observers has a physical meaning, and they state that Shapiro answers "yes" it does. Question (1) above is answered "yes." This answer comes from Shapiro himself (according to Taylor and Wheeler) and it is included in Taylor and Wheeler's book, so it seems pretty mainstream. Question (2) above is answered "mainstream."
Taylor and Wheeler then analyze the Shapiro delay. They state that it is too awkward to integrate the equation for the "skimming" path of light next to Sun that the Shapiro experiments actually use [page E-2]. So they state that:
Instead we obtain an estimate of the delay time by assuming a slightly different path . . . that comes in radially from Earth, circles halfway around Sun in a tangential semicircular path, then moves out radially . . . This alternative path . . . yields an estimate much closer to a precise calculation than we might have expected. [page E-2]
They use an illustration like the attached.
They then calculate the delay as a combination of the radial and semicircular segments. The calculation uses the radial Shapiro delay formula, as does Iggy. Taylor and Wheeler's slightly different path generates a delay very close to the actual delay determined by experiments (approximately 250 ms modeled delay for a roundtrip to Mars). This is a delay "reckoned by remote observers" [per Taylor and Wheeler, page E-1], so it is in fact the coordinate speed of light measured by distant observers [as phrased by xyzt]. So, the coordinate speed of light is the valid explanation of the Shapiro delay. The answer to question (3) above is "yes."
Going back to Taylor and Wheeler's introductory questions to the project, and answering them:
* What happened to "Light always moves with the same speed"? [light travels slower near gravity as measured by distant observers, which has real physical meaning]
* Who says light slows down near Sun? [shapiro, for one, according to Taylor and Wheeler]
* How much does light slow down near Sun? [approximately 250 ms for the Earth-Mars round trip]
* Does observation verify the predicted value of the slow-down? [yes]
2 -
As an analogy, if someone sat near the event horizon of a black hole with rockets firing at enormous acceleration in order to hold their position then they would see the universe above them unfold at an extremely rapid rate. Light would move from one side of a galaxy to the other in an instant (from their perspective). If they set themselves up as the origin of a coordinate system then they'd need to account for time dilation to account for the increased coordinate speed of light above them.
I agree with this. What I did in the other exercises was to proportionately adjust all of the clocks' tick rates to the same rate (the farther rearward, the more elapsed ticks show on the clock than actual ticks of time for that rocket's clock). I think that you would call this putting all of the clocks on the same coordinate time. That eliminates the time dilation effect. It leaves only the distance effect. If you calculate the speed of light using the proper distance, then you get the speed of light slowing the closer the rocket is to the rear of the accelerating row (or the deeper in a gravitational well).
I think that xyzt objects to that description:
Once again, this is the coordinate speed of light, an entity devoid of any physical meaning. As explained already in post 3, this entity can take any value (in GR, it is dependent on the coordinates
Having heard from a lot of members who have been kind enough to respond, and done a lot of reading, I think that it is reasonable to consider two descriptions to be true. First, the speed of light is constant. In gravity, the distance that one is measuring when doing a Shapiro delay experiment is greater when the sun is between the earth and the other planet than when the the sun is not. The greater time that the experimenter on earth measures in the former case is due to the fact that the distance is greater. Second, in the earth experimenter's frame the speed of light is not constant; the speed slows when the sun is between the earth and the other planet. Call this the coordinate speed of light; that is fine. But it is not "devoid of any physical meaning." It is measurable by the earth experimenter. We cannot simply change our coordinates to get another value -- we live on earth, we send signals out into space, and we need to take this effect into account when doing calculations that depend on the amount of our proper time that passes before the signals return (or before the signals reach a spacecraft that we have sent into space).
Here is an excellent example of the two views, both from the same person. Neil Ashby is responsible for the GR corrections in the GPS system: http://en.wikipedia.org/wiki/Neil_Ashby
Here is a piece that he coauthored about GPS corrections: http://www.gps.gov/cgsic/meetings/2012/weiss2.pdf
This notes that there are relativity terms that are becoming important in the GPS system. Slide 2 describes two effects that are not currently used in the GPS corrections: "Signal Propagation Delay" caused by "Earth's Gravitational Field." The first of the two is expressly called the Shapiro delay on slide 15. So, one way of looking at the effect is that gravity causes signal propagation delay, which I think can fairly be interpreted only one way -- that gravity slows down the signal (delaying something is slowing it). If we want to make the GPS system more precise, we would need to correct for this signal delay. It has physical meaning; we live on the earth, drive our cars here, shoot guided missiles at each other here, etc. So we cannot deny the physical reality or importance of this signal slowing.
On the other hand, Ashby also says (from the other perspective) that the effect is one of greater distance: the distance is the coordinate distance plus the "so-called" Shapiro delay (slide 3). So it seems to be fair to view the question from both perspectives, at least if you want to be able to both understand GR and build an accurate GPS system.
1 -
I get the same, thanks, and I apologize for getting the question numbering wrong (and for stipulating that the ships accelerate at 0 rather than 60 in their frame, making it a bit awkward). I will put together a Minkowski diagram shortly and think about your question about the time it takes for the ship to pass, but here is a summary and finishing off of question 5.
The ships initially present 80 apart in the ground frame, with their clocks not synchronized there. The rear (Bert) clock is ahead by the product of velocity and proper length, hence 100 * 0.6 = 60. Events that are simultaneous in the Bert/Frank frame (like clock striking 60) are not simultaneous in the ground frame. Events at the rear happen 60 units of Bert/Frank time earlier in the ground frame than events at the front. So Frank's clock reads 0 and Bert's 60 in the ground frame.
Now let's assume simultaneous acceleration in the Bert/Frank frame at their time 60 (since Bert is already at 60, and we don't want to have to go back in time . . .). Bert accelerates first in the ground frame (his clock reads 60 at inception). It takes 60 units of Frank time, with Frank traveling at 0.6, before Frank accelerates. That is a head start in the ground frame for Bert of 75 units of ground time, so Bert closes 15 of the separation in the ground frame as you calculated, leading to a 65 distance in the ground frame when Frank accelerates (thus ending Bert's head start and locking in the 65 ground distance).
During Bert's head start, he is traveling at 0.8, so his clock ticks slower in the ground frame than Frank's. As you note, Bert's clock ticks only 45 while Frank's ticks 60. The new gamma for Bert is 1.667 (because he is traveling at 0.8), and 75 ground time / 1.667 = 45. Thus, at the time Frank accelerates, Bert's clock reads 105 in the ground frame (60 at the start, plus 45). Frank's reads 60. The difference in clock times in the ground frame is 45 as you note.
The proper distance between the ships is the ground distance times gamma, or 65 * 1.667 = 108.333. Both ships are at rest with respect to each other (in the same reference frame). If the clocks are still synchronized in their frame, then Bert's should be ahead of Frank's in the ground frame by the product of proper distance and velocity, or 108.333 * 0.8 = 86.667. But it is only ahead by 45. So Bert's clock has fallen behind in their frame.
So, the example shows that:
Ships that accelerate at the same rate cannot maintain their proper distance. The proper distance increased by 8.333 in the example. The front ship has to accelerate at a lower rate to maintain proper distance. If the two ships accelerate Born rigidly, then they will maintain their proper distance at all times. Consistent with another post above, same proper distance at all times = at rest with respect to each other at all times = in the same reference frame as each other at all times = agree on simultaneity with each other at all times.
Their clocks will run at different rates in their own frame, admittedly. As the example shows, the rear clock actually runs at a slower rate in the ships' frame (thinking about this leads to the equivalence principle, with Bert being lower in the gravity well than Frank). But if they accelerate Born rigidly, with Frank accelerating at a lower rate than Bert, they can maintain their proper distance, stay at rest with respect to each other, remain in a common reference frame, and as a result agree on the simultaneity of events.
0 -
Getting back to the initial posts, I will go out on a limb and say that yknot is not nuts.
There are three events: (1) emission of light, (2) light striking O1, and (3) light striking O2. The light emission and the light strikes are all events, and serious physicists would agree. Witness Taylor and Wheeler, Spacetime Physics, page 10: "Another event is the emission of a flash of light from an atom . . . A fourth event . . . is the strike of a lightning bolt on the rudder of an airplane." See also the (less august) wikipedia entry on "Spacetime": "Events which occur to . . . a photon along its path (i.e., while traveling at c, the speed of light), all have light-like separations." yknot correctly described the events that occur to the photons (striking the observers) as events, and correctly described them as being light-like events (perhaps better to say, like wikipedia, that they have light-like separation).
Also, it is not necessary to have a second light source to show the relativity of simultaneity (although Einstein uses one in the train example, and admittedly yknot is using the train example). All you need is a light source that flashes spherically outward. Then, when the light strikes observers who are equidistant and on opposite sides of the light source in its frame, the strikes will be simultaneous in the light source's frame. But they will not be simultaneous in other frames that are in motion relative to that frame. See Spacetime Physics at page 176.
yknot, in your original post you say that the two strikes are absolutely in the order O1 first and O2 second because they are light-like. But it is not the case that all events that have light-like separation occur the same order in all inertial reference frames, as Taylor and Wheeler show. I agree with the early responses that the relative motion is important, and that it is fundamentally what special relativity is all about. If you use a second light source on the opposite side of the observers, or if you separate the two observers slightly at inception and put the light source between them, there will still be differences in how the observers observe the light (just as you point out in your original post), but as the other posters say this just illustrates special relativity. It is not inconsistent with SR.
0 -
This site says 20% of all humans who ever lived past age 65 are alive today:
http://www.trinity.edu/mkearl/ger-biol.html
So I suspect you have to go a lot higher than age 50, perhaps age 90 or 100.
0 -
md65536,
Here is a good exercise to start to work through the questions. It uses instantaneous acceleration, even though it cannot generate exact Born rigid motion (and even though many scientists say instantaneous acceleration is not physically possible). It comes up with answers between Born rigid motion and Bell's spaceship paradox. But it has the advantage of simplicity.
Start with Bert (back ship) and Frank (front ship) at rest with respect to each other, separated by 100 in their frame, their clocks synchronized in their own frame showing time 0, and in inertial 0.6c motion relative to the ground. Q1: how do they present in the ground frame (what is the ground distance between them, and what does Bert's clock read in the ground frame if Frank's clock reads 0 in the ground frame).
Next, at their time 0 and simultaneously in their reference frame, each accelerates instantaneously to 0.8c relative to the ground.
Ground frame questions:
Q2: in what order do they accelerate in the ground frame? Q3: how much ground time passes between the first of them accelerating and the second of them accelerating? Q3: how much ground distance apart are they when both have accelerated? Q4: what does each clock read in the ground frame at the instant that the second of them accelerates?
Ships' frame questions: After their accelerations (which were simultaneous in their own frame), when they are both at rest with respect to each other and in the same frame in inertial movement relative to the ground at 0.8c:
Q5: how far apart are they in their own reference frame? Q6: are their clocks still synchronized, and if not whose clock is ahead in their frame, and by how much?
0 -
The generally given answer is that the object length contracts in the observer's reference frame from the object's rear forward. A good way to think about it is to use the relativity of simultaneity and an object already in motion relative to the observer. The object accelerates simultaneously along its length in its own frame. That is not simultaneous in the observer's frame. The acceleration at the rear occurs first in the observer's frame, then the accelerations of each remaining part of the object occur successively later and serially from back to front. So the farther back along the object, the greater the head start in acceleration in the observer's frame. So the contraction occurs from the rear forward.
If you want the object to start at rest and then accelerate, here is a good illustration of the rear forward contraction:
0 -
It is possible for a row of objects to accelerate and maintain their proper distance in a single shared accelerating reference frame, although there is a limit of front end acceleration for a given proper row length beyond which rearward parts of the row cannot keep up and so fall behind (and out of the others' frame). A good explanation is here:
http://www.mathpages.com/home/kmath422/kmath422.htm
A very comprehensive article (behind a pay wall) is Taylor and French, "Limitation on proper length in special relativity," Am J Phys 51 (10), Oct 1983, page 889.
0 -
Thanks. Hopefully someone with full GR math skills can help us

Is it possible to run the actual numbers and compare them? Here is a stab at the numbers for acceleration.
Assume an elevator that is 1LY wide, at rest in an inertial frame. Light is flashed into the elevator horizontally at time t=0. Simultaneously, the elevator begins to accelerate upward at 1g, which I believe is 1.0326 LY/Y/Y. In the inertial frame, the flash takes 1Y to strike the opposite wall. In 1Y, an object accelerating at constant proper velocity 1.0326 LY/Y/Y travels 0.4236 LY in the inertial frame. So an observer in free float in the elevator would observe that the light was bent, with a total 0.4236 movement downward for 1.0 movement across.
Is this a fair way to interpret the accelerating elevator in the equivalence principle? Can anyone confirm or correct those numbers? If they are correct, how do they compare to what GR shows to be the amount of bending in a homogeneous 1g gravitational field?
It turns out that there was already a thread covering the question of the amount of bending, although it does not seem to have reached consensus. It is here: http://www.scienceforums.net/topic/64305-why-does-light-bend-during-acceleration/
0 -
So, what does the Andromeda Paradox add to the age-old and never ending philosophical debate on determinism, free will, and all that? Nothing. At least that is my opinion. Per the physics as we know it, the only events I can see / observe / measure are those that are on or inside my past light cone. The only events I can somehow influence are those that are on or inside my future light cone. My "now" lies in that no-mans land of uninfluenceable, unobservable events that lies between my past and future light cones.
Here is a different version of the paradox that may illustrate DH's view.
If an earthling's acceleration to a high velocity toward Andromeda causes Andromeda's distance to length contract and its clock to advance (in both cases in the earthling frame), then a subsequent earthling deceleration should cause Andromeda's remaining distance (after reduction for the earthling's actual travel during the acceleration and deceleration) to length expand backward, and its clock to regress. But you can't turn back time by decelerating, and so you cannot always reconcile the earthling and Andromeda reference frames.
Consider a rocket and a probe that are at rest with respect to each other 100 apart (example uses consistent unitless dimensions, such as years, light years, and light years per year^2). The probe is programmed to self destruct at probe time Tp=99.8. The rocket and probe have clocks set at the same time 0 in their common rest frame. The rocket then accelerates at proper rate 300 for probe time Tp=0.07, then decelerates at the same rate back to rest over Tp=0.07. In the inertial probe frame, very little happened. The rocket began and ended at rest, and it traveled probe frame distance Xp of only Xp=0.133, in only Tp=0.14 (all calculations are based on the relativistic rocket formulas from http://math.ucr.edu/home/baez/physics/Relativity/SR/rocket.html). The probe is nowhere near exploding.
In the rocket frame, the acceleration takes rocket time Tr=0.0125 (significantly less than Tp=0.07 because of time dilation). If the distance to the probe contracts and the probe clock advances per the formulas above, then the probe clock reads Tp=99.82 to the rocket at the end of the acceleration. During the rocket's acceleration (specifically, at Tr=0.0121), the probe reaches its programmed destruction time and blows up in the rocket's frame -- and then for an additional Tp=0.02 scatters some debris (but not the core) in all directions (including some toward the rocket), and sends a flash of light from the explosion in all directions (including toward the rocket).
Next, the rocket decelerates in its frame over Tr=0.0125, and ends at rest only 0.133 closer to the probe than at the start. What happens in the rocket's frame to the flash of light from the explosion? What happens to the debris? Does the probe reassemble and race backward during the deceleration? Debris that flew forward cannot distance expand backward to meet the core, because the expansion should be proportional (like the contraction). The light flash that went forward also cannot distance expand backward to disappear into the core for the same reason. Yet the rocket has returned to rest and rejoined the probe in a common frame, and the probe is unexploded in that frame when the rocket has returned to rest in that frame.
0 -
Thanks for all of the responses. To follow up:
ajb, do you have thoughts on Einstein's counterfactual thought experiment? Assume that gravity is homogeneous (1g whether you are here, 100 km higher, or 100km to the right, etc.). Then would that make it globally impossible to tell that you are in gravity?
xyzt, I don't think that IM Egdall is disputing that GR gets the bending of light right. He suggests that the amount by which light bends in the elevator is wrong -- light does not bend enough in an accelerating elevator, so an occupant of the accelerating elevator can tell that he is not in a gravitational field. The problem with the form of the equivalence principle as quoted above is not that an elevator occupant can observe anything unusual when the elevator is at rest in a gravitational field and he is falling downward; it is that he can observe something unusual when he is in free float and the elevator is being accelerated upward.
Length contraction is important in this case because the observer can measure the distance between (a) where the light started out horizontally at one wall, and (b) where it strikes the opposite wall after bending. If the walls are not only moving upward (which gives the observer the sense that he is falling), but also length contracting upward, the length contraction will have an independent effect on where the light hits the opposite wall. This might cause the light to strike the wall at a different place than it does in the case of an elevator at rest in a homogeneous gravitational field.
Again, this is no argument about GR. Everyone agrees that GR shows the correct amount of light bending in the case of gravity. The question is, does the accelerating elevator frame get the wrong amount of bending? If it gets the wrong amount of bending, then the broad equivalence principle quoted above is not globally correct. But the reason that it is not globally correct is not because of something that the observer measures due to gravity. It is because of something that the observer measures due to acceleration. The other examples I give of length contraction or proper length expansion are just other ways that an observer in free float can tell that an elevator in which he lives is being accelerated.
It should be possible to determine whether the light flash hits the opposite wall in the same place in an elevator at rest in a gravitational field as in an elevator undergoing constant acceleration, at least in the case of actual (non-uniform) gravity (because the GR formulas describe actual gravity). I don't know whether it is possible to compare the results of homogeneous gravity versus constant elevator acceleration.
Toffo, let's push the question a bit further. Are you using homogeneous gravity or actual gravity? Also, say the observer carries his own meter sticks. Does the light bend the same amount in his meter sticks in both the gravitational field and the accelerating elevator? If the light hits the same place on the wall in both cases, it might be because of the offsetting effects you describe, which means that the observer could use his own meter sticks to determine that light bent a different amount in the two cases, so the two frames are not equivalent.
It would be great to be able to make the equivalence principle true globally by restricting it to the case of homogeneous gravity. But it seems that the accelerating reference frame has a lot of unique features that an observer can actually identify, which would mean that you cannot make the principle globally true that way.
It also raises the issue about how to define locality in the more narrow definition of the equivalence principle that ajb utilizes. It is not enough to restrict your measurements to a small enough region of spacetime to avoid being able to measure tidal effects. You also have to restrict yourself to a small enough region of spacetime to avoid being able to measure the effects of acceleration on the elevator. You have to restrict to the lesser of the two. Although I do not know which requires a smaller area.
0 -
A typical objection to the equivalence principle is that you can tell that you are falling in gravity because you can see that an item falling alongside you compresses horizontally and stretches vertically. However, this results from tidal effects of non-uniform gravity, whereas Einstein stated the equivalence principle very clearly to apply in the case of homogeneous (that is, uniform) gravitational fields. See post here, http://www.scienceforums.net/topic/79255-distinguishing-between-acceleration-and-gravity/?p=772228, and Einstein quotation from 1907:
We consider two systems S1 and S2… Let S1 be accelerated in the direction of its X axis, and let g be the (temporally constant) magnitude of that acceleration. S2 shall be at rest, but it shall be located in a homogeneous gravitational field that imparts to all objects an acceleration –g in the direction of the X axis. As far as we know, the physical laws with respect to S1 do not differ from those with respect to S2; this is based on the fact that all bodies are equally accelerated in a gravitational field. At our present state of experience we have thus no reason to assume that the systems S1 and S2 differ from each other in any respect, and in the discussion that follows we shall therefore assume the complete physical equivalence of a gravitational field and a corresponding acceleration of the reference system.
Quoted at: http://www.mathpages.com/home/kmath622/kmath622.htm
So it seems that the typical objection is wrong, and it may not be possible to identify anything in S2 that is distinguishable. Is there anything that you can identify in S2, given a homogeneous gravitational field, that is distinguishable?
Alternatively, if the equivalence principle does not hold true over extended spacetime (but only over small local spacetime), then is the reason because of something identifiable in S1 (the accelerating frame), rather than S2 (the frame at rest in a homogeneous gravitational field)? Consider someone in a really tall Einstein elevator in space (far from any gravitational mass). The elevator is accelerated upward relative to him at a constant magnitude for a very long time before the floor comes up and strikes him. He observes the walls and everything on them racing upward past him and thinks that he is falling down in the elevator. Here are two potentially identifiable things in the upwardly accelerating elevator that could distinguish it from an elevator at rest in a gravitational field. Are they correct? Do they distinguish acceleration from gravity over extended spacetime, such that the equivalence principle can hold only in small extensions of spacetime?
1. It has been suggested that the degree to which light bends in the accelerating frame is less than that which light bends in equivalent gravity. See post here: http://www.scienceforums.net/topic/67141-equivalency-principle/?p=684962. The "falling" observer could theoretically determine this by measuring the light bending and the rate at which his speed relative to the walls grows. Then S1 and S2 would be distinguishable. Does this occur, so would it distinguish the two reference frames?
2. Accelerating the elevator at a constant magnitude raises Bell's spaceship paradox issues. If you accelerate all parts of the elevator at a constant rate (same magnitude over the entire height of the elevator, which is equivalent to length in this context) then the elevator will keep its same height in the "falling" observer's frame rather than length contracting; the observer will notice this (contrary to the elevator at rest in a homogeneous gravitational field, which an observer falling within it should observe as length contracting upward toward him). Also, the accelerating elevator would increase in proper height, and it would tear apart (which the "falling" observer would note).
If instead you accelerate the elevator's parts in a Born rigid manner, the bottom will accelerate at a greater rate in the observer's frame than the top, so the elevator should length contract at a greater rate than the elevator at rest described above (which the "falling" observer could presumably measure). And, if the elevator is really tall (such that its proper length is greater than c^2 divided by the proper acceleration of the top end), then even Born rigid acceleration will not prevent the elevator's proper height from expanding, and the elevator will tear apart toward its bottom. The "falling" observer will be able to observe this. Does any of this occur, such that it could distinguish the two reference frames?
0 -
Xyzt, I will have to leave it to someone else to do the mathematical proof you request. Hopefully Iggy has time.
Separately, though, I think that two of your posts are inconsistent.
In post 81 above, you say the following about two particles accelerated the way that we call Born rigid: "the only correct claim he makes is a trivial one 'A and B agree at all times on their common velocity'. Yes, this is obvious, so what?" This seems to say that the two particles share a "common velocity," which is to say that they have the same velocity.
In post 94 above you say that we "are dealing with three particles that all have different speeds in any frame you consider". This implies that the no two of the particles share a common velocity.
Do the particles have a common velocity, or not, in your view?
0 -
Here is a recap and a reopening of the question of the coordinate speed of light in the accelerating frame as a function of the distance from the rear (which should be like the distance from a gravitational mass). I think that the result utilizes parts of the posts from each of md65536, Iggy and xyzt.
As md65536 suggests, consider a row of separate ships at rest in an inertial frame that are then simultaneously accelerated (rather than trying to accelerate a single object that has the same length as the row). Each ship accelerates at a proper rate inversely proportional to its distance from the origin. For example, the ship that starts at x=0.5 accelerates at a=1/0.5, or a=2. The ship that starts at a=1 accelerates at a=1/1, or a=1. As Iggy states, under these conditions the ships undergo "Born rigid" motion: they remain together in a shared accelerating reference frame; they keep their same proper distance in that accelerating frame; they agree on simultaneity; they always have the same velocity relative to the inertial frame; and their worldlines in the inertial frame are hyperbolas. Their clocks do not run at the same rate in their frame. The farther forward a ship is, the faster its clock runs. However, the rate is proportional to distance, so each ship behind the front can program its clock to automatically scale up its elapsed time proportionately and thus keep its clock synchronized with the front clock. Iggy advises that the front clock's time is the conventional measure of time in the accelerating frame; it is called the coordinate time of the frame. The time that we measure in that frame when we determine the speed of light in the frame is coordinate time, and so I think that the speed of light in that frame is its coordinate speed.
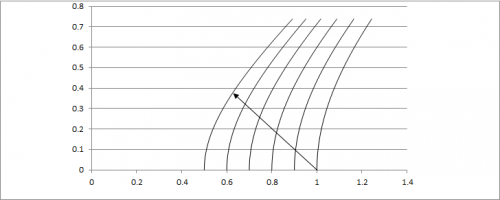
As the ships start to accelerate, the front ship flashes a light toward the rear. The Minkowski diagram for the inertial frame is as follows (ships' worldlines are hyperbolas; light flash's worldline is the arrow):
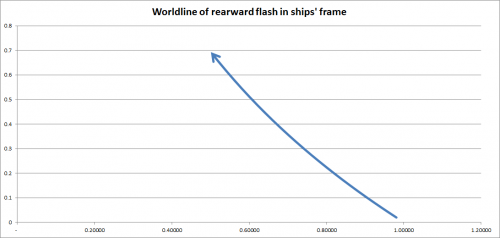
Because the ships are all in the same (accelerating) reference frame, we can Lorentz transform the light's path into the ships' frame. The light's worldline is no longer a straight 45 degree line. Rather, it is curved:
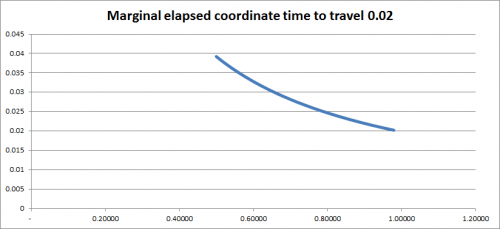
To make the effect clearer, we can diagram the marginal amount of coordinate time that it takes for the light to travel successive equal segments in the ships' frame (here done using distance increments of 0.02). It takes successively greater coordinate time to travel equal segments the farther toward the rear of the row (left in the diagram) that the light is traveling. In coordinate time, light is always traveling less than c, and increasingly less as it moves rearward:
Notice that the curve flattens out toward the front of the row (toward the right). This suggests that the coordinate speed of light over successive equal increments is higher toward the front (the right), but at a decreasing rate. It suggests that the coordinate speed will not exceed c. This agrees with xyzt, who states that the speed of light is not proportional to the distance from the origin, and more specifically that the speed of light will not exceed c at distances farther away from the rear. Xyzt prefers not to use calculations, but Iggy you can confirm that the coordinate speed of light does not exceed c as follows.
Start with two ships, one at x=99.98 and the other at x=100. They accelerate simultaneously and flash a light at each other. Their acceleration rates are 1/99.98 and 1/100, respectively. Next, as you did before use the relativistic rocket formulas to determine the coordinate time that each light flash takes to cross the 0.02 proper distance and strike the other ship. You should find it to be 0.020002 (same in both directions). The coordinate speed of light is still less than c (0.02/0.020002), but it is getting very close to c. This is just an example, but I expect that those of you with better math skills than I have can prove that at any distance away from the origin the coordinate speed will remain below c (I think that it will asymptotically approach c, but I cannot be sure).
1 -
Here is one approach (which I think follows the alternative you mention that one might not be able to separate out the slow ticking from the effect of changing simultaneity), along with a couple of citations objecting to it.
In order for there to be relative motion, someone has to accelerate. When he accelerates and gains speed, the other frame length contracts toward him, and a row of clocks laid out along the length of the other frame desynchronizes because of the relativity of simultaneity. The more distant the clock is from the accelerated observer, the farther ahead in time it will present in his frame after the contraction. Think of the clocks in the other frame as odometers, spinning up as they length contract the original distance toward the accelerated observer. The farther away a clock originally was, the more distance it has to cover in the contraction to keep the contraction proportionate -- so the more distant the clock the more it contracts toward the observer and the more it advances in the observer's frame, like an odometer advancing as a vehicle moves a great distance. Each clock thereafter ticks slower in the observer's frame, but each successive clock that he passes is ahead of the prior one. The net result -- the clock advancement effect exceeds the slower ticking rate, so as the observer passes along the row of clocks in the other frame and reads their times in series, they run (as a series) faster than his clock. Every clock in the other frame remains synchronized in that other frame (because that frame did not accelerate), so time is passing faster throughout that frame (including for a stay at home twin) than it is for the accelerated observer. This clock advancement effect is from our other discussion at: http://www.scienceforums.net/topic/80036-relative-aging-without-acceleration/, which has links to more detailed explanations, including the use of this to explain the twin paradox.
That said, others object to this concept of clock advancement. See for example this response to the claim that the clock advances as described above and explains the paradox:
"No, I am as against quick advancing of the clock (I called it scrolling) from 7.2 years to 32.8 years as I am against the clock being 7.2 years one moment and 32.8 years the next." from http://www.physicsforums.com/showthread.php?s=c51bf4a98b8d0910836daef7b994a123&t=257843&page=3
Here's another that seems to object to the concept, based on the view that the math does not work out:
"The point of using an abrupt acceleration (and long outward and return journeys) is that the amount of clock-advancement that the earth observer /might/ see during the turnaround acceleration stage can't possibly compensate for the timelag that builds up in the coasting stage, unless the earth observer sees clocks going backwards or signal overlaps or some other sort of apparent breakdown of visual causality that's not supposed to happen in current theory." from http://sci.physics.relativity.narkive.com/YPFnUziq/what-killed-special-relativity.2
I find that the math always works out if the accelerated observer completes the trip along the row of clocks, but there are some issues if he does not. Say the observer accelerates quickly to a very high speed, then just as quickly decelerates back to rest. The clocks in the other frame would advance as described above with the acceleration, then regress with the deceleration (actually spin backwards in the decelerating observer's frame). This seems unusual. The final difference in proper clock times between the accelerating observer and the stay at home twin depends on the amount of time that the accelerating observer spends at speed, so a quick acceleration followed by a quick deceleration will not generate very much final difference in proper time between him and the stay at home twin -- yet it seems to lead to a lot of clock advancement followed by clock regression, which does seem odd.
0



Sagnac explanation question
in Relativity
Posted
I agree that it is tough, but that is part of what makes it interesting. The light emitter and the photographic film that recorded the fringe shift were fixed on Sagnac's rotating disk, so what he recorded was from the POV of the rotating disk, not the inertial frame attached to the center. Trying to understand the effect from the POV of the disk is worthy of effort.
And I agree, the c+v and c-v refer to closing speeds.
If the observers on the rim try to synchronize their clocks using the Einstein convention sending signals in one direction, then yes I think that each clock is ahead of the one behind it (or vice versa, if the signal were sent in the other direction). I don't know, however, what is simultaneous with what if you synchronize clocks with any given convention (a light signal from the center, or some other method). I am not sure what simultaneity convention properly applies to a rotating rim. So I was focusing first on the explanation of the Sagnac effect; if the closing speeds of the signals measured on the disk relative to their source (on the disk) are the same as the closing speeds of the signals in the lab frame relative to their source (on the disk), i.e. c+v or c-v, that might give some information to help with the subsequent question of simultaneity. But it seems as if the closing speeds are different on the disk.