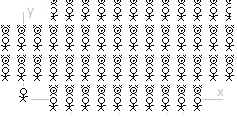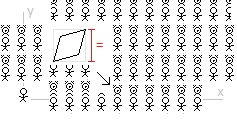Thales et al

Awesome! The first link is exactly what I've been looking for. (And thank you for the rounding out my knowledge of the available internet resources with the second link!) I would have up voted your last post twice but it only let me do it once. Thank you. [Opps. I keep forgetting my old account on Science Forums and then sing up for a new one, but then I forget that my browser might remember my old account and so I sign in with my old account after I've started a question under my new account. And ... yes, yes, yes ... I know Science Forums does not allow multiple accounts to prevent "sock puppetry" and so I know I'm not allowed to have multiple accounts. Please delete "Thales et al" I no longer have that email account and I don't remember the password of that account for this forum (even if my browser does remember it). Sorry for breaking the rules.]

madmac, There are clocks (with observers) at every theoretically possible point in the “original observer’s” inertial frame of reference. And all of these clocks, in the inertial frame of reference of the original observer, are synchronized. (Perhaps we can call him the “OG observer.”) All of the “clock/observers” are requested to report the “event” of the part of the square that is right next to him at one specified time (such as “12:00:00”). And so, when 12:00:00 rolls around on all of the synchronized clocks, one of the clock/observers will say the top right corner of the square is next to him and another will say that at 12:00:00 the lower left corner is next to him and so on (and not just for the four corners but for every point along each side there will be a clock/observer at 12:00:00 who can report what “event” is next to him at this time). And this way we can find out the “height” of the length contracted square in the inertial frame of reference of the “original observer.” (If the square is moving at a constant relative speed this this same “height” will be found no matter what agreed upon time we use (11:59:59 or whatever).) And the same thing is done for the “height” (the y displacement) of the vertically moving rectangle. This is why I don’t think “Relativity of Simultaniety” is the solution here. (I’ve tried but I still don’t see it.) The clocks that are relevant to the measurements here of the square and rectangle are in the rest frame and so are not un-synchronized. (But it’s possible that when we switch to the square’s rest frame or to the rectangle’s rest frame this “relativity of simultaneity” with the square or the rectangle then pops up from this switch and saves the day (paradox-wise) … but I can’t see it yet.) However … After reading your link Mike-from-the-Bronx … I may be able to start seeing this other way to the solution. I’m definitely not there yet … but I think I’m beginning to understand the basics of the kind of switching (double-switching) you are talking about. I’m still thinking … I can start to see something. Thank you. And thank you all!

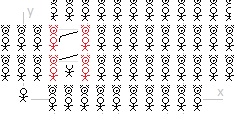
Right. I understand that now. When I was first thinking about this idea, I was thinking that "relativity of simultaneity" had no relevance here (and I said as much in some previous posts). I don't understand how this "paradox" is resolved yet, but I understand that it has to do with "switching frames" and the "relativity of simultaneity" and "the square/diamond losing its square/diamond" shape. Again, I don't understand (yet) how this all works and how this "paradox" is then resolved ... but I will ... thank you (and everyone else) for the direction. By "what is missing is a lattice of clocks" I believe is "what is missing" in my OP in terms of madmac's question. - In the Wikipedia link to "Thomas precession" it reads: "Although Thomas precession (net rotation after a trajectory that returns to its initial velocity) is a purely kinematic effect, it only occurs in curvilinear motion and therefore cannot be observed independently of some external force causing the curvilinear motion such as that caused by an electromagnetic field, a gravitational field or a mechanical force, so Thomas precession is usually accompanied by dynamical effects.[1" In this thought experiment ("the diagonal motion paradox") there is no external force ... right? When we go from looking at this from the "third observer's" frame of reference and then looking at this from the square's frame of reference there is a "shift" that takes place. It is a "shift" in perspective. There is no "external force" like that from an "electromagnetic field" or from an "gravitational field." Does "Thomas precession" apply to this thought experiment? I am confused. - - I’m trying to understand “relativity of simultaneity” as it relates to this “paradox.” One thing that can be noticed, is that if the square has four clocks, one on each corner, and if it is moving diagonally, then while the four clocks will be all synchronized in the square’s inertial frame of reference, with the diagonal motion, in the “third observer’s” inertial frame of reference the square’s two clocks perpendicular to the direction of the motion (A and B) will be synchronized while the leading clock © will be behind A and B and the trailing clock (D) will be ahead of A and B. Am I on the right track for a resolution?

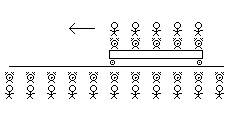
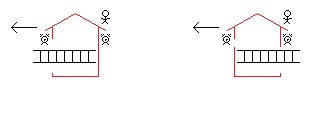
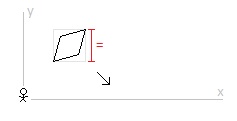
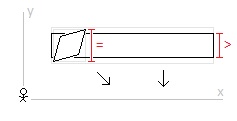
madmac, I believe I can answer your questions. You are right that it takes time for light to reflect off an object and then reach the observer’s eyeballs. I made the mistake in my OP of just talking about “the observer.” In these kind of thought experiments the idea is not that there is only one observer or only one observer per frame of reference. I was using the term “the observer” to distinguish his frame of reference from the frame of references of the square and the rectangle. What is missing from my OP is the idea of a “lattice of clocks.” If we were trying to do something as simple as see how long a moving car is in the frame of reference of the road at rest and how long the car is in the frame of reference of the car at rest, we would need a lattice of clocks with an observer next to each clock. And we would need a lattice of clocks (with observers next to them) in the road’s rest frame and in the car’s rest frame. (Obviously, no matter how close the observers are to each clock it will take an amount of time, very very small perhaps, for the light reflected clock readings to reach the observer’s eyes. But, it’s my understanding that the professional academics just kind of allow for this to be so small so as to be reasonably ignored.) And, yes, just as in the drawing above where there are observers in both frames of reference, in the OP, I should have included observers in the square’s frame of reference and observers in the rectangle’s frame of reference (as well as more observers in, what I’ve been calling, “the observer’s” frame of reference). And so, there are some times when things appear to perhaps violate the Special Theory of Relativity. For example, if someone had a laser pointer and moved it across the night’s sky really fast someone could try to make the claim that it is moving faster than the speed of light from one distant body in the night’s sky to the next. But, if you could make this argument, it’s only an argument about appearances. Nothing is actually moving faster than the speed of light. If I understand Special Theory of Relativity “paradoxes” right, then they are only true paradoxes if the paradoxical thing is actually happening physically. If it only appears to be a parardox, it is not. And if it is actually a paradox (occurring in physical reality), but doesn’t appear that way, it still is a paradox. I hope what I’ve said here addresses what you were getting at. Bottom line: I should have included a whole bunch of clocks (with observers by each one) in the “observer’s” frame of reference as well as in the square’s and rectangle’s frame of references. And I should have stipulated that all of the clocks in the observer’s frame of reference are synchronized with one another and all of the clocks in the square’s frame of reference are synchronized with one another and all of the clocks in the rectangle’s frame of reference are synchronized with one another. (The Special Theory of Relativity allows for clocks in the same inertial frame of reference to be synchronized.) Sorry for the confusion.

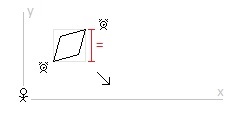
Okay … maybe I am wrong. If a square is moving diagonally across an inertial frame of reference is that square’s height knowable? Is the square’s height one thing if we look at it one way and is the square’s height a different thing if we look at it a different way (at the same time in the same inertial frame of reference)? If that’s what I’m hearing that doesn’t seem right to me. It seems like the square’s height and the rectangle’s height should be knowable and solely based on their direction of motion relative to the given inertial frame of reference. And so, it seems to me that in the inertial frame of reference of the observer the height of the diagonally moving square should stay the same and the height of the vertically moving rectangle should decrease. But … that would mean a paradox. I’ll keep studying! Thanks for the links!

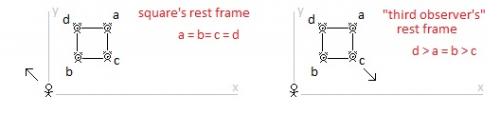
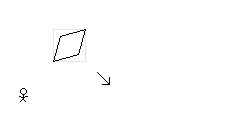
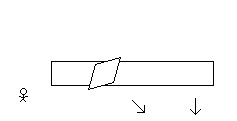
In the observer’s frame of reference, the square’s motion is diagonal. However, we can talk about the vertical component of the square’s velocity and the horizontal component of the square’s velocity. It is my understanding of the Special Theory of Relativity that length contraction only occurs in the moving body’s actual direction of motion. It is my understanding of the Special Theory of Relativity that length contraction does not occur in a moving body’s “component” directions. No? The square is moving diagonally and so it should contract diagonally. The square has a component of its motion moving vertically, but it does not (… or so I believe …) contract vertically. Nor should it contract horizontally. “Moving bodies contract in their direction of motion.” Am I right? "The key I would focus on is that a square contracted diagonally in 2 steps does not have the same shape as a square contracted diagonally in 1 step. That's how it still fits in the rectangle." Can we do length contraction like this? Am I wrong that length contraction occurs in the direction of overall motion of a body?

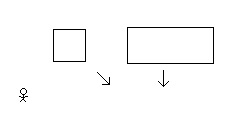
Alright … first things first … the most important question first … are you really from the Bronx? “Switch reference frames from initial setup to Third Observer. Rectangle now moving diagonally(with additional contraction). Square now moving diagonally (with contraction). Third Observer at rest.” In the third observer’s inertial frame of reference the rectangle is moving vertically (not diagonally) but the square is moving diagonally. In the third observer’s inertial frame of reference the rectangle is contracted vertically and the square is contracted diagonally. Well, at least that’s what I tried to say. More questions? And thank you for taking my idea here seriously. If there is a way to use “relativity of simultaneity” to resolve this “paradox,” I can’t see it. 1. Clearly in the square’s rest frame the square remains within the rectangle. 2. And clearly in the rectangle’s rest frame the square remains within the rectangle. And so, It must be that in the observer’s rest frame the diagonally moving square also remains in the vertically moving rectangle (… for there not to be a paradox). And so I suppose you could say that the bottom of the diagonally moving square is inside the vertically moving rectangle but at an earlier time and the top of the diagonally moving square is also inside the vertically moving rectangle but at a later point in time? But this leads to the contradiction of the diagonally moving square being both longer and shorter (in its y dimension) at the same time (in the inertial frame of reference of the observer). Using relativity of simultaneity in this way would mean contradicting basic relativistic length contraction. As far as I can tell, in the inertial frame of reference of the observer the length contracted square is outside the bounds of the length contracted rectangle. ?

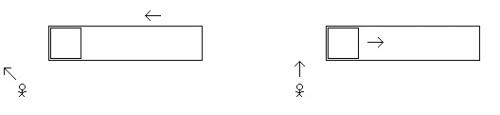
Hello Mike from the Bronx, I’m from Mesa. “but the rectangle will have diagonal motion and be a parallelogram. You don’t show that.” Right. In this thought experiment, three frames of reference are noted: the observer, the square, and the rectangle. If I were to add more frames of reference there would be a frame of reference in which the rectangle is moving diagonally and so it would contract diagonally in that frame of reference. In the three frames of reference noted here, however, the rectangle happens to not be moving diagonally in any of them. In the observer’s frame of reference the rectangle is moving vertically, and so it contracts vertically. In the square’s frame of reference the rectangle is moving horizontally, and so the rectangle contracts horizontally (… and the square remains within the rectangle). In the rectangle’s frame of reference the square is moving horizontally, and so the square contracts horizontally (… and the square remains within the rectangle). The Special Theory of Relativity, as I’ve come to understand, leads us to some weird conclusions, … but … in the end whatever happens in one frame of reference (e.g. the square colliding with the rectangle) must also happen in every other frame of reference (e.g. the square cannot not collide with the rectangle). We can look at this from the perspective of the rectangle moving diagonally. But, it seems to me just looking at this from the perspective of the observer vs from the perspective of the square (and rectangle) there is already a problem. No? I am always willing to learn! Hello studiot! In the ladder and barn “paradox” the two clocks in question are in motion (… from the perspective of someone at rest relative to the moving barn). And when clocks are in motion “leading clocks lag.” And so, the ladder is within the closed barn doors even though the ladder is too long to fit but it’s able to do so due to synchronized clocks in one inertial frame of reference not being synchronized in another inertial frame of reference. In this thought experiment (the “diagonal motion paradox”) the height of the square is not being measured by moving clocks in the square’s inertial frame of reference. The two clocks in the drawing above, … measuring the length contracted square … are necessarily in the observer’s frame of reference. The observer measures the square based on clocks in his inertial frame of reference and not based on clocks in another (the square’s) inertial frame of reference. And since the two clocks are in the observer’s inertial frame of reference, the Special Theory of Relativity allows for them to be synchronized (… for the observer). No? Please advise!

In the ladder/barn/pole "paradox" the ladder and the barn doors only encounter each other at a specific moment in time. The ladder moves through the one door and then the ladder moves through the other door. Here, time is not necessarily a factor. This thought experiment could be modified to say "the square and rectangle are moving like this relative to one another over 1 billion year" or "the square and rectangle are moving like this relative to one another over an infinite amount of time" If there is a way to get the square to break through the rectangle in the square's rest frame and if there is a way to get the squrae to break through the rectangle in the rectangle's rest frame with "time" and with "non-synchronous events" I haven't been able to do that yet. But, perhaps you seem to have made it work. I don't know.

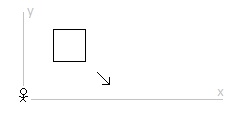
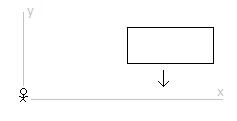
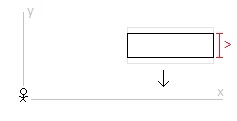
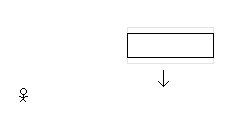
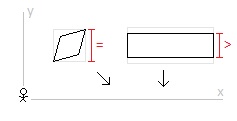
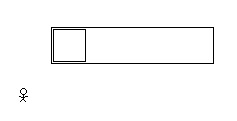
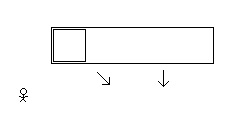
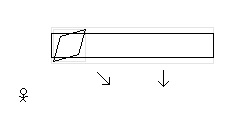
There is a square moving at a constant speed across an inertial frame of reference. Relative to an observer at rest in the inertial frame of reference the square is moving diagonally. The moving square is length contracted in its direction of motion. (A diagonally moving square is diamond in its direction of motion. Contracted, it becomes a rhombus.) And so, from the perspective of the observer, the height of the diagonally moving and length contracted square is the same when it is at rest or when it is in diagonal motion. There is also a rectangle moving at a constant speed across this same inertial frame of reference. Relative to the same observer the rectangle is moving vertically. The moving rectangle is length contracted in its direction of motion. And so, from the perspective of the observer, the height of the vertically moving rectangle is less when in vertical motion than when at rest. From the perspective of the observer, in the inertial frame of reference of the observer, the height of the diagonally moving square in motion is the same as when it is at rest and the height of the vertically moving rectangle in motion is less than when it is when at rest. The square is inside the rectangle. When at rest, the height of the square is slightly less than the height of the rectangle. The square moves diagonally down and to the right. The rectangle moves straight down. The vertical component of the square’s velocity is the same at the rectangle’s vertical velocity. The moving square contracts in its direction of motion. The moving rectangle contracts in its direction of motion. (The velocity of the square is more and so it contracts more in its direction of motion.) The height of the square remains the same when at rest. And the height of the rectangle decreases. And so, with the height of the square only slightly less than the height of the rectangle when at rest, then, assuming the velocities relative to the observer are considerable, the length contracted square will be beyond (break through, depending on the materials) the bounds of the length contracted rectangle. The Special Theory of Relativity predicts, in the inertial frame of reference of the observer, the square will not remain within the walls of the rectangle. 1. From the perspective of the square at rest, where the rectangle and the observer are in motion, does the square remain within in the rectangle or does the square break through the rectangle? 2. From the perspective of the rectangle at rest, where the square and the observer are in motion, does the square remain within the rectangle or does the square break through the rectangle? 3. Does the square break through the rectangle in one inertial frame of reference while the square remains with the rectangle in other inertial frames of reference? 4. Is this a paradox?

This thread ended a long time ago. But I found a page that includes a pretty good description of what is physically happening in the Ives-Stilwell experiment. http://spiff.rit.edu/classes/phys314/lectures/doppler/doppler.html And so I figured I'd post it here if anyone is interested. Cheers!

Okay. I think I'm starting to get it. Thank you all for helping me out!

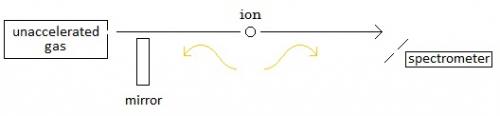
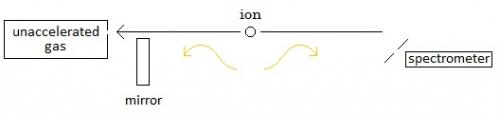
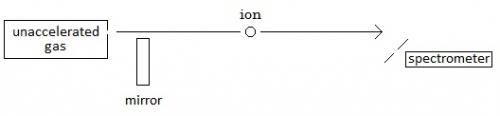
zztop: This is my current drawing: In my drawing the positive ion moves from the container on the left to the spectrometer on the right. However, you said: “1. Light coming directly from the ion is redshifted because the source (the ion) is moving AWAY from the receiver 2. Light going into the mirror has the same frequency as the light reflected from the mirror (due to the energy conservation). So, light reflected by the mirror into the receiver is blueshifted because the source (the ion) is moving TOWARD the mirror.” And so I’ve changed my drawing: (I changed the arrow on the moving ion from left to right to right to left) Is this now right? If so, then this clears up my red-shift/blue-shift confusion. Cool. But, then … if this is correct … my basic understanding that the ion comes out of the container of gas … and so would then move from left to right is all askew. My question (simple, like all of my previous ones): how does the ion end up moving from right to left? (This is so simple, I know it must be dumb.) Thank you.

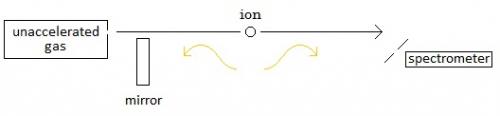
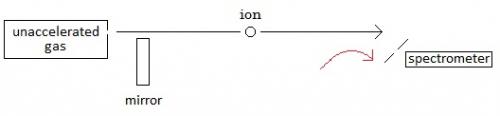
Cool. More progress. Okay, in my drawings the grate and the spectrograph are left pretty much untouched/unexplained. I want to get to their description, but I still have a question about what has been said up to this point. I have a question about what is in my drawings in post #17: I show the light coming from the ion and to the receiver as red-shifted and I show the light coming from the ion and to the mirror (and then to the receiver) as blue-shifted. But shouldn’t it be the other way around? Shouldn’t it be that the light coming from the ion and moving in the same direction as the ion is blue-shifted and the light coming from the ion and moving in the opposite direction as the ion is red-shifted? No? Thank you!

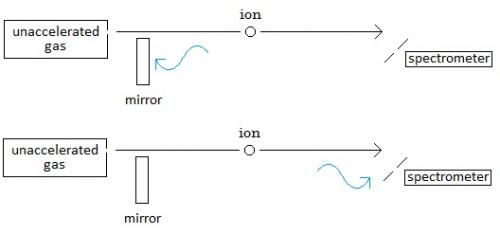
zztop,I reread post #13, and if I’m reading it correctly now, that means I misread it before. This is what I’m now thinking. Please correct me where I’m wrong. --- Positive ions move from the gas filled cathode towards the spectrometer. The ions emit electromagnetic waves (light). Some of these move towards the spectrometer. And some of these move in the other direction towards the mirror. The waves that have come directly from the moving ion (the waves that were emitted in the same direction as the moving ion) arrive at the spectrometer red shifted. And the waves that first bounce off of the mirror (the waves that were emitted in the opposite direction as the moving ion) arrive at the spectrometer blue shifted. The amounts of red and blue shift are measured and compared. The amount of red and blue shift from the Doppler effect from the velocity of the moving source can be calculated. If this calculated amount is removed from the measured amounts, then what we are left with is the amount of additional red shift due to relativistic time dilation. --- Do I have this right? Please let me know. And please correct me where I’m wrong. And thank all of you for helping me with my problem.