

Tassus
-
Posts
12 -
Joined
-
Last visited
Content Type
Profiles
Forums
Events
Posts posted by Tassus
-
-
-
0
-
A Correction: After the 5th line (at the previous picture), replace v->+infinity with y->+infinity
Thank you all for your help!
So according to your comments, I sum up:
see the attached picture.
0 -
-
So, the application of this approximation to the Gamma function is independent of the number set that the argument of Gamma belongs to? i.e. wether the argument is natural or real number etc
Thank you!!!
I guess you can just apply the Stirling formula listed below to get the desired result.
[Remember that x!=Gamma(x+1)]
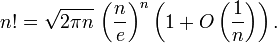 0
0 -
-
Ι think that the derivatives are the following, Is there anyone to confirm this?
Assume A= A' and B=B' then
φ(τ) = ln(det(τΑ+λΙ))
φ'(τ) = tr(τΑ+λΙ)-1A
ψ(τ) = tr(τΑ+λΙ)-1B
ψ'(τ) = tr(τΑ+λΙ)-1B(τΑ+λΙ)-1)A
ψ''(τ) = -2tr(τΑ+λΙ)-1B(τΑ+λΙ)-1)A(τΑ+λΙ)-1)A
0 -
I see no reason to expect a simple or elegant expression for the derivatives that you seek.
Take a look at simple case, say 2x2 diagonal matrices, and see how messy the expression is. It gets uglier from there.
I think that there must be some expressions in terms of traces, determinants and things like that, notice that in the special case where λ=0 the function φ(τ) = ln(det(τΑ))=ln(τkdet(A))=klnτ+lndet(A) so the first derivative for example is just k/τ. So for the general problem I think that it can be written in a compact convenient form, for example in case of 2x2 matrices (k=2) φ(τ)=ln(τ2det(A)+λτtr(A)+λ2) which is an expression where the derivatives can easily be derived.
0 -
I hope someone could explain how to calculate the following derivatives,
Assume A, B are kxk full rank matrices I is identity matrix of the same order and τ is a nonnegative scalar variable and λ real number then define the following two functions
φ(τ) = ln(det(τΑ+λΙ))
ψ(τ) = tr((τΑ+λΙ)-1)B
which are the first and second derivatives of φ(.) and ψ(.) w.r.t. the argument τ?
A proof and/or references should be usefull.
Thank you
0 -
This looks a lot like a homework question. We generally don't provide complete answers to such things.
Perhaps you could explain what you've done so far? People will be more inclined to help then.
Basically what I want to do, is show that anexpression that involves traces is bounded. A is a Positive definite matrix and B is either positive definite or positivesemi definite (it depends on the assumptions of the other matrices that included in B, which I it set so for convenience). Ithink I can show it by the fact that tr(AB)>0 or tr(AB)>=0.
0 -
Hi, I would like some help with this,
Assume A and B nxn matrices
1. If A,B are positive definite matrices what about the sign of tr(AB)?
2. If A is positive definite and B is positive semi definite what about the sign of tr(AB)?
Thanks!
0

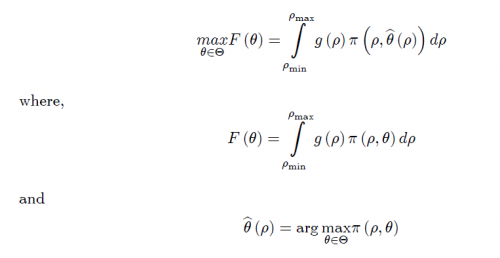

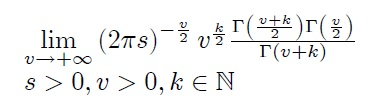
The maximimum of a Functional
in Analysis and Calculus
Posted
Please see the updated version:
Under what conditions can we state the following?
[latex]\max_{\theta>0} F \left( \theta \right)= \int_{\rho_{min}}^{\rho_{max}} g \left( \rho \right)\pi\left(\rho,\widehat{\theta \left( \rho \right)} \right)d\rho[/latex]
where,
[latex]F\left ( \theta \right )=\int_{\rho_{min}}^{\rho_{max}}g\left(\rho \right )\pi\left(\rho,\theta \right)d\rho[/latex]
and
[latex]\widehat{\theta\left( \rho \right)}[/latex] is the argument that maximize [latex]\pi(\rho,\theta)[/latex] with respect to [latex]\theta[/latex]
Let [latex]\rho_{min}=0[/latex] and [latex]\rho_{max}=1[/latex]. Assume also that [latex]g(\theta)[/latex] and [latex]\pi(\rho,\theta)[/latex] are proper unimodal densities of [latex]\rho[/latex] and the parameter [latex]\theta>0[/latex]
Alternatively, we can state the problem in the following way: Determine the conditions that satisfy
[latex]\max_{\theta>0} F \left( \theta \right)= \int_{0}^{1} g \left( \rho \right)\max_{\theta>0}(\pi\left(\rho,\theta \right))d\rho[/latex]