little boy

HCI _(s) <=> H⁺_(s) + Cl^-_(s)

Is there many kinds of infinity? e.g. some infinity is larger that other infinity

 

such as lim x->0, 1/x=infinity and lim x->0, 2/x=infinity

 

both are equal to infinity, but actually the "second infinity"=2*"first infinity"

Are there any alternative computing engine of WolframAlpha?

the video is wrong and misleading! They play trick!

 

The two series start at the same time.

 

That means the upper"2" doesn't start with the lower"-2", instead it start with lower "-1",

 

and then after you cancel out the upper number and lower number,

 

that will be 1+2+4+8....... (the same as the original one),

 

then you get the right answer as infinity!!

 

I think the above is the simplest way to explain. Is it helpful?

The denominator of the main fraction is undefined and and the answer should be zero, as 1/undefined = 0

 

"undefined" has no meaning, how does it result in 1/undefined = 0?

Kind of but not really, it depends how you look at the reaction. Read this link, it gives a good explanation of the limitations using your example.

 

Truth be told, the Arrhenius definition is inherently limited in its application. Generally we consider amines as acting as either a Lewis base, since amines can donate a lone pair of electrons, or as a Bronsted-Lowry base (which is more or less the same as the Arrhenius definition, but not as limited), as they can accept H^+.

 

The page states :

 

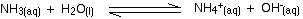
"Nevertheless, there are hydroxide ions there, and we can squeeze this into the Arrhenius theory."

so I think it is Arrhenius base

Is NH₃ a Arrhenius base? I don't know whether a Arrhenius base requires a OH^- in the molecule.

wow.. very detail

Could you perhaps provide some more context? Are you asking this in terms of chemical reactions?

 

yes, They are chemical reactions.

Is it legal to simplify

a->b->c as a->c

a <=> b <=> c as a <=> c ?

Why is NH4Cl(aq) acidic and CH3COOHNa(aq) basic?

It's infinite.

 

I said it is not a limit, and it is 1/(1/0), not 1/0.

1/(1/0)=? (not limit)

 

Is it zero or undetermined?

 

w=R1, x=R2, y=R3, R4=z, s=R5, v=voltage of cell, a=voltage of point A, b=voltage of point B, then,

 

Inputting"a-(a-s*((v-a)/w-a/x))=s*((a-s*((v-a)/w-a/x))/z-(v-(a-s*((v-a)/w-a/x)))/y), solve a" on wolframalpha, then a is found

 

 

Inputting"(s*(b/z-(v-b)/y)+b)-b=s*((v-(s*(b/z-(v-b)/y)+b))/w-(s*(b/z-(v-b)/y)+b)/x), solve b"on wolframalpha, then b is found

 

 

It is certainly correct as I have tested it many times.

I had been calculating it for about 6 hours.(so crazy..... )

How is V1-V2 (stage 3, point 6) used in calculation? Why is it needed to know?

 

clear image

 

I even didn't know it is called bridge circuit, therefore I had not searched the internet. Now I found a possible solution.

 

voltage A=V[R2/(R1+R2)], voltage B=V[R4/(R3+R4)]

 

It is deduced by My link, please check whether I am correct.

Assuming the voltage of the negative terminal is 0, how calculate the voltage of point A and B? And can anyone draw a simpler equivalent circuit for me. God bless the people helping me.

 

picture

 

beside, why am I not allowed to use the image extension on this board?

The first thing to realise is that long after the switch is closed the current through the capacitors will cease to flow( they will have accepted all the charge they can). This means that after that time you can ignore the capacitors when you calculate the voltages across the resistors. When you look at it this way, the resistors are in series and the formula used is correct. This is the standard voltage divider formula. http://en.wikipedia....Voltage_divider

 

what happen after the switch is closed? I am confused.

It might help to look at the circuit like this:-

 

Thank, now I am clear

 

How does it deduce that V1=R1/(R1+R2) x V while R1 and R2 are not in series? (highlighted)

 

image link

R1 and R3 are in parallel and together are in series with parallel R2 and R4.

 

Then it is incorrect to say that R1 and R2 are in series?

My link Is it correct to say that R1 and R2 are in series , R1 and R3 are in parallel? God bless the people answering me.

 

Is there a simpler equivalent circuit?

now I understand, thankyou

My link This is a the page of my exercise. After the switch is moved to position B, it says a parallel circuit is established, but circuit seems not completed because one terminal of the cell is not connected.

God bless the people answering me.

What is electric breakdown? Can anyone explain it briefly? The results from Google are too complicated and not understandable.