Rian00077

-- In general: -- In fact, I did not change the definitions of the classical parameters (time, mass, etc.), but introduced the corresponding generalized parameters with similar names. These generalized parameters fully include the classical ones (and their numerical values), but are more informative. This is due to the fact that they are described by more than one real number, unlike the usual ones. That is, several real values correspond to a vector (complex numbers also have this property). For example, the classical mass corresponds to a "projection" generalized to a specific axis (for more details, see paragraphs 2a, 2b, 2c). And the classical time shift corresponds to the modulus of the time vector in A1. -- Example: -- An example of how this works, Consider a transition between reference frames that uses this time difference and depends on mass (Fig.). We have the law of additivity for the es-vectors that define the system: s0 + s1 + s2 = 0 (vector form) Where s1 and s2 are the es-vectors from for an arbitrary point (or rather an object, which is important with a certain mass) s0 is the es-vector between reference frames (their centers) It is the modulus of the parameters in A1 (s-vectors, time, etc.) that are directly used in the calculations, and their direction is determined directly through this modulus, for simple geometric reasons. That is, having the modulus of the es-vectors s1, s2, and s0, we precisely define the corresponding triangle with our objects at its vertices (this is the use of the spatial additivity of the es-vector). Next (all for the module), s1 = m1 t1 s2 = m2 t2 Where m1 and m2 are the "projections" of the mass of an arbitrary object on a perpendicular plane to the directions of the s1 and s2 vectors, respectively. From the law of conservation in A1 (point 2b): m12 u12 = m2 c2 m22 u22 = m2 c2 u1 and u2 are the "rms projections" of the mass of an arbitrary object on a perpendicular plane to the directions of the s1 and s2 vectors (more detail about u definition in the file or shortly above). And accordingly, u12 = c2 - v12 u22 = c2 - v22 Where v1 and v2 are the projections of the object's velocity on the s1 and s2 axes of the vectors, respectively. In total, it turns out: s1 = m t1 /(1 -v12/c2)1/2 s2 = m t2 /(1 -v22/c2)1/2 Then we can express t2 through t1. -- Time difference an its relationship to mass: -- Now what do these t1 and t2 mean. These are distances in classical space, more precisely, if multiplied by c; r=c*t (from the definition of time in A1), r is a classical distance. As you can see, these distances are different for different reference frames (according to Lorentz transformations). More precisely, the space (of these classical distances) is different for different reference frames. And it is precisely the mass that affects whose transition between systems that will determine this curvature of space. The fact is that classical space is not affected by mass at all. That is, the classical distance to an object is not affected by its mass, which is consistent with common understanding. Therefore, to determine the classical distance, the time vector itself in A1 is used, not the es-vector (which corresponds to this "ignoring of mass"). These "usual ideas" stem from the fact that we (with the eye) determine the distance to an object through the movement of light from it (i.e., through the time of this movement) and do not take into account the internal structure of this object, i.e., its mass (we do not take it into account for distance). The es-vector takes into account mass, which is why it is an invariant. By defining everything through the es-vector, we also get this "multiplier" of mass near the time in A1 (and, according to the previous considerations, near the classical distance). And it is this multiplier that deforms space during transitions. We can find these spaces and, accordingly, this deformation as follows. We have defined the spatial location of objects in A1 through the modulus of the es-vectors and their "spatial adjacency" (i.e., through the triangle, etc.). We can also define the location in a classical (non-invariant) space. Only for this purpose, instead of the modulus of the es-vectors, we need to use the modulus of the time vector in A1. Which were expressed in the formulas above. And the distortion of the modulus of the time vector (compared to the es-vector) due to this "multiplier" of mass will lead to a different placement of objects and just the same deformation (Lorentz transformation). The "time shift" for different reference frames is expressed by finding the change in the location of objects over time in each reference frame. This is done using the formulas described above. And then we divide the displacement by the velocity, etc. * time motion is determined by the velocities used in the formulas. Here we consider an example without force interactions and acceleration. ------ I could give a lot of specific examples, but I was afraid to write even more text (though it would be less if I only could know that my file was read ... but I maybe shouldn't expect ... that anyone would read it). (What I have directly stated is a relatively short summary that came at the end, so it should not be directly understandable) Do I write too much?

I forget to quote, so your answer is above. it's just that it's big, so I don't want to duplicate it.

... Alright, but how should i post these over than 10 pages (with figures and formulas) ... here? So, perhaps the way for it somehow related with a forum post system, but i don't know how. Thank you for saying that, because a lot of people didn't read it for that reason. Although, I can publish a short version of this theory here (but it will be too unclear; in this case, the full version is needed), --------------------------------------------==== == Full functionality of the A1 == I will summarize how the system will work in the complex === 0) Everything in A1 is defined in terms of es-vectors: s = m· t where m is the mass for the corresponding direction, which determines the "projection" of the internal energy of the object to the perpendicular (relative to s) direction. This energy is kinetic in nature, which was converted to internal energy to consider the "perfectly straight" motion of the object (to avoid the ARM of the direction). t is the time vector, which is responsible for both classical space and time. The correspondence to classical space is straightforward, i.e., it is enough to multiply the time vector by the speed of light (r = c·t ). The correspondence to classical time is more conditional. In short, the modulus of the time vector corresponds to the time difference of objects (connected by a vector), but to get the exact value, you need to take into account the ratio of the masses of these objects (i.e., simply multiply by it). === 1a) The es-vector is an invariant (unlike time or mass), as is the whole of A1. Moreover, A1 is completely relative in terms of parameters, and does not require direct transitions between reference frames. That is, we can say that it has all the necessary parameters at once. 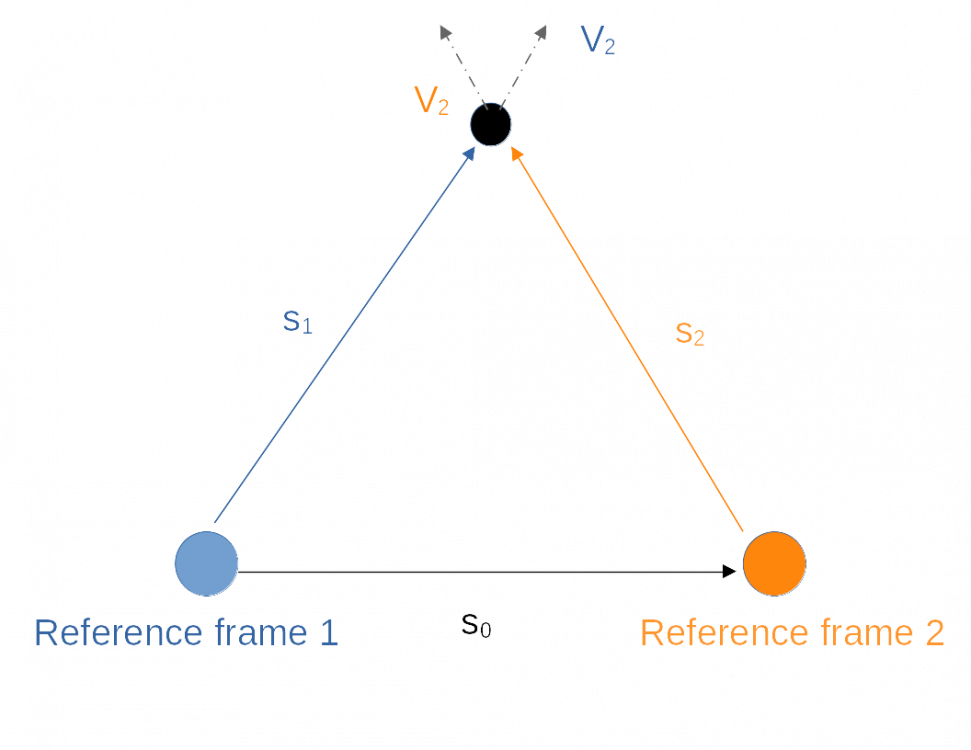=== 1b) Also, the s-vector has classical spatial additivity. That is, if you imagine drawing a contour in space and it returns to the starting point, the sum of the s-vectors "on the way" will be zero (s1 + s2 + s3 + … = 0). === 1c) In accordance with the homogeneity of classical time and space, the s-vector varies linearly in time. That is, the first derivative of the es-vector in time is a constant*, although time itself depends on the point of view (i.e., the analog of the reference frame in A1). By the way, these descriptions describe both the homogeneity of classical time and space. * The acceleration of classical space occurs due to changes in mass. === 2a) In A1, there is a more specific definition of mass. Based on this idea of "additional indefinite motion" (AIM), we can define mass more precisely. Mass is a characteristic of an object's inertia, i.e. how difficult it is to change its speed. And as a result of AIM, a particle gains additional inertia and energy. To find this energy, it is enough to find the rms velocity in the perpendicular direction. In this representation, the particle always moves at the speed of light. The projection (of the speed of light) on the principal direction will be the classical speed. The projection on the perpendicular plane will determine the additional inertia. Fig. This additional "energy" is equal to E0 = m0^2 · u0^2 , where u0^2 is mean square in the perpendicular plane m0 is the mass corresponding to this direction (different for each). Moreover, E0 is a constant, the same for all directions and equal: E0 = m^2 · c^2 where m is the classical rest mass of the particle Also for geometric reasons: υ^2 + u0^2 = c^2 , υ is the classical velocity (projection on the principal direction) As you can see, m0 can be determined if we know υ (and E0 ). Note that it is the mass of m0 that is taken into account when determining the es-vector (the direction of which is the main one). Now the usual mass change with speed is displayed: u0^2 = c^2 – υ^2 m0^2 = E0 / u0^2 = m^2 · c^2 / u0^2 = m^2 / (1 – υ^2/c^2) m0 = m / (1 – υ^2/c^2)^1/2 Energy in A1 is responsible for the kinetic energy that has been made internal (thereby increasing the mass). That is, when we simplify* the trajectory of a particle, we neglect some of its movements, which takes away some of the kinetic energy. Which, according to energy considerations, is converted into mass. Here it is the law of conservation of energy (conservation of the sum of internal and kinetic energy). * for example, to a straight line, to determine the speed *. Given that these "simplifications" of the trajectory depend on the direction, the mass also depends. And other considerations described above (about mass). === 2b) This leads to an alternative law of energy conservation. The classical law can often coincide with the law of mass conservation. But here the mass is determined separately for each direction. In this case, the following product is always conserved: E0 = m02 · u02 = m2 · c2 (where m is the classical rest mass of the particle) This product is the same for all directions. And the "conservation" of this product is an alternative law of energy conservation. As you can see, this total energy E0 in A1 uses only invariant parameters, so E0 itself will be invariant. That is, the energy in A1 does not depend on the reference frame or the particle with respect to which the parameters are taken. (E0 = m0^2 · u0^2 , where u0^2 is the rms velocity, m0 is the mass corresponding to this direction) Let me remind you that in the s-vector, the mass is taken for the perpendicular direction relative to the direction of the s-vector itself. When in the law of conservation of energy, the mass is taken for the same direction (or plane) as u0^2 (Fig.11). === 2c) In fact, when transitions between frames of reference, there is a redistribution of speed (rms). From the direct speed of υ to the additional u (and the total one is equal to this). Energy for each direction is also collected, which can be seen from formulas. The fact that in the energy the square of mass appears A1 is a consequence of the fact that everything is expressed here in general through the es-vector and conditionally through its derivatives in time. The square of mass is a reflection of these dimensions. And what about the fact that the law if not for linear (which contradicts what I said earlier). Then at the base it is linear, just the very concept of velocity that is shown in it is based on a discrete representation of particles. Because of this, the law takes on this form (although in fact it is linear). === 3a) The effect of additional motion is also important. No matter how hard we try to get to the center of mass of the system, in practice the "real "* center of mass will be circling around somewhere. But for some unknown reason, the "law of space" (s1 + s2 + s3 + … = 0) will not work perfectly. Although the amplitude of these additional oscillations is determined by the mass. This effect is not actually chaotic, but rather a consequence of the "oscillations" of the universe itself. These oscillations are in fact "ordered and organic", not chaotic. Only the complexity of these fluctuations is difficult to describe with the usual mathematical apparatus, because they are fluctuations of the whole universe. === 3b) In total, all the work in A1 is work with the s-vectors of different systems (and their intersections), and the definitions of mass and time. But because of this effect, we cannot exactly match the s-vectors (i.e., the end of one with the end of the other). As a result, we know the s-vectors between objects, but we cannot know exactly between which objects they are drawn. That is, these objects may not completely coincide as systems of particles (i.e., not all particles will coincide). === 3c) By the way, it can be noted that, given the linearity of all laws and formulas here, the whole of A1 is completely analogous in continuous or differential form. It is enough to replace the mass with its density in the s-vector and then integrate it. === 4a) Also, in A1, there is a key possibility of "collapsing" an arbitrary set into a system. Only in A1, no matter how inaccurate the information is (about the location of particles, their motion, etc.), there will always be a system (set of elements) for which the s-vector will have a specific numerical value. This property is evident from the definition of the s-vector. Moreover, it is important for this property that the description in terms of s-vectors is complete. This property follows from the following. If our information is approximate, then when it is expressed in terms of s-vectors, their value will be limited in some region, in the space A1. In this case, this area can be "collapsed", i.e., the value of the s-vector for the system corresponding to this area can be determined. This will be the value of the s-vector for the center of mass of this system, i.e., as if for the "center of mass of our inaccurate information". Logically, it will have a specific value. === 4b) By the way, all prerates in A1 do not have to be real numbers. All formulas and reasoning are valid for any type of number. That is, they can be complex numbers, etc. (i.e. numbers of the next order of complexity after the complex one). === 5a) One more thing about the center of mass. As you might have noticed, its definition (m1 T1 + m2 T2 + m3 T3 + … = 0; (T1)^2 = (T2)^2 = (T3)^2 <=> |T1| = |T2| = |T3| = T ) may not give solutions for a large number of particles. That is, for two particles, one dimension is enough to locate the center of mass, for three particles, a two-dimensional space will be needed, for 4 particles, three dimensions, and then ... , there will not be enough dimensions. So the point is that these restrictions are for a really significant T, and it can be any (complex, etc.). === 5b) Now about force interactions and acceleration. And here, it turns out, there is no need to introduce something new to describe it. The acceleration (and, accordingly, the force) is a consequence of the change in the mass of the particle. That is, as I said, the s-vector snakes linearly. And if the mass does not change, then the time vector will change linearly as well (I remind you that we are talking about the acceleration of the classical r = c·t ). But when the mass of the particle changes, the time vector will not change linearly. This directly determines the acceleration. === 5c) To describe this acceleration, it is enough to use only a part of the object's mass in the es-vectors (s = m· t ; Δs = Δm· t). Then you can split each object into parts. Now we will have several systems with their own centers of mass (Fig. 10). Let's assume that everything in the refined model is linear (es-vectors, motion of the centers of mass). Then if the centers 2 and 3 move relative to each other, there will be a redistribution of masses in the simplified model (due to the averaging of masses, because the mass will be shifted to one of the particles). And, accordingly, acceleration in the simplified model. Although in the refined model everything was linear. That is such a breakdown can be used to define force interactions, while still maintaining linear motion of the es vectors and everything else. ------------ Just a reminder that this is only the short version. The full version is on the file (and, probably, it is better to read it first) Ghideon, I apologize for the delayed response, The thing is that I distinguish between two concepts related to the speed of light. The first is photons. Of course, I did not mean that they do not exist. I only meant that a photon (like any other object) cannot have completely zero mass. But it can be as small as possible (which corresponds to reality). It's just that if we take into account the conservation law in A1, the complete zeroing of mass will lead to the zeroing of u0 (which cannot happen in AIM). The same law shows that when the rest mass tends to zero (and therefore u0), the translational velocity v will tend to the speed of light (which corresponds to the photon) And the second (which you asked about) is the phenomenon of the motion of the boundary of each particle at the speed of light. This is a mathematical boundary in the form of a sphere with a particle in the center. On this boundary, the mass density tends to zero, which corresponds to the definition of "boundary". And accordingly, its speed tends to c. In fact, the first concept corresponds to ordinary light, which literally glows. It is a more conditional concept, so it depends on the "appearance" (color, etc.) of the luminous object. Therefore, it is formed in a less uniform (discrete) way, i.e. by photons, as particles. And secondly, it corresponds to the concept of light as a speed of information transmission. It is not formed by photons and is not discrete. But it is responsible for the movement of that "boundary" and, accordingly, the exchange of information between particles (for example, about their existence, time delay, and mutual placement). It is also responsible for the relationship between time and space and their homogeneity. That is, with homogeneous time, space is formed so that the "boundary" is spherical. * Note that only the "boundary" can have a velocity equal to c, and not just be moving towards it (photons). Of course, given the presence of other particles, this boundary is not directly "visible". But given the linearity of A1, its position is still determinable. I hope I have answered your question. (You probably meant that I should have derived the photoelectric effect in a different way). ...a lot of text, but it's just not in the file.

Please, take a look at a theory I've created. This is the theory about a different space and time definition. I've really tried to take this work as seriously as possible. And will be glad to get any feedback. Here I will consider a slightly different interpretation of space and time, and try to describe how the world will look like in it, and how different laws will work. The theory based on this another interpretation (I will call it A1) is analogous to classical spacetime. But in it, in addition to the placement (of particles, objects, points, etc.) in a "space", it is also possible, through the properties of this "space" in A1, to set the laws themselves. That is, the laws of interaction between objects that allow us to fully describe the world and its change over time. A1_v1.0.pdf