

Z.10.46
-
Posts
69 -
Joined
-
Last visited
Content Type
Profiles
Forums
Events
Posts posted by Z.10.46
-
-
yes, but there's nothing preventing transitioning from an approximation to an equality, for instance, if π~3 then I can state that π=3+a with a=π-3, thus If the symbol ~ gives you trouble, then I can even avoid using the integer part to make it an equals sign: if n/ln(n)~N and (n+2)/ln(n+2)~N+1, then n/ln(n)+a=N and (n+2)/ln(n+2)+b=N+1, with a and b being real numbers .
So, if there exists an infinity of twin primes, the equation (n+2)/ln(n+2)+b=1+n/ln(n)+a would have a solution where n is very large. If this equation does not have a solution for very large n, then there exists a finite number of twin primes that are less than a specific n..
0 -
Hello,
I have π(x)~x/ln(x), the larger the value of x, the more true this relationship becomes.
Suppose I have two very large twin prime numbers, then I would have n/ln(n)~N so E(n/ln(n))=N and (n+2)/ln(n+2)~N+1 so E((n+2)/ln(n+2))=N+1 with Using E to denote the floor function.
So, if there exists an infinity of twin primes, the equation E((n+2)/ln(n+2))=1+E(n/ln(n)) would have a solution where n is very large. If this equation does not have a solution with a sufficiently large n, then there are a finite number of twin primes that are less than a specific value of n.
This equation is true only if I have infinity = 1 + infinity,So, twin prime numbers are infinite.For your information: When proving the infinitude of prime numbers, it is also demonstrated through this type of equation: q = p1 * p2 * ..{pi}.. * pn + 1/pi. It is stated that the only possibility for q to be an integer based on this equation: infinity = infinity + 1/Pi. Thus, we conclude from this that prime numbers are infinite.
And similarly, to demonstrate an infinity of twin primes, I also use the equation infinity = 1 + infinity.0 -
What is the mathematical equation in 2D and 3D for your body?
Is there a mathematician in our world who could find the mathematical equation in 2D and 3D for their own body?
For your information, 2D refers to surface equations, and 3D refers to volume equations.
This passage is just for laughter and to encourage participants to try finding the equation for their own body:
It's amusing that no mathematician has thought of writing their own body equation, who knows perhaps this equation hides a great mathematical secret.😀
Some legends about the city of Atlantis mention that the foundation of their highly advanced civilization, far more advanced than ours, lay in the discovery of these equations of the human body...😉
It's a buzz that can be noticed by many people, even those who aren't mathematicians. If a mathematician could find the equation of their body, it would create a significant buzz. They could gain notoriety and might even be paid by celebrities and wealthy individuals to write their body equations as well...🤑
0 -
3 minutes ago, Bufofrog said:
I thought you weren't suppose to bring this up again.
I have corrected the unit of measurement problem, so now the mathematical formulation of the theory is 100% correct. Now, I am seeking your opinion on how to interpret it.
0 -
Yes, but they have a total negative energy -m0c^2.
That can explain dark matter or dark energy, as we can see its negative energy effect after this transformation by this phenomenon...
-3 -
Hello ,
The present theory explores the behavior of the expression of relative mass M(v) with respect to the speed of light (v=c)\ and suggests that dark matter or dark energy could be composed of ordinary particles with mass that have reached the speed of light.
The theory delves into a mathematical analysis of the series representing the relative mass function, M(v), and discusses its divergence at v=c, drawing parallels with the regularization of the Casimir effect using the Riemann zeta function, which gives M(c)=-M(0) at v=c.
It proposes the existence of a natural phenomenon that accelerates ordinary matter with mass to the speed of light and transforms it into dark matter or dark energy with negative relative mass and finite energy.1.Representation of the Divergence of Relative Mass at v=c:
Consider the function of Relative

2.Application of zeta function regularization on the divergence of relative mass at :
You can just separate off the divergent part of and define it via zeta function regularization.
Define:


4.Representation of the Divergence of Relative energy at v=c:
Due to the definition of the energy-momentum four-vector, in particular its time coordinate, we end up with the expression of the total energy of the particle in the laboratory reference frame, that with respect to which the particle is animated with the speed v because the energy depends on the frame of reference in which it is calculated!) in the form of:
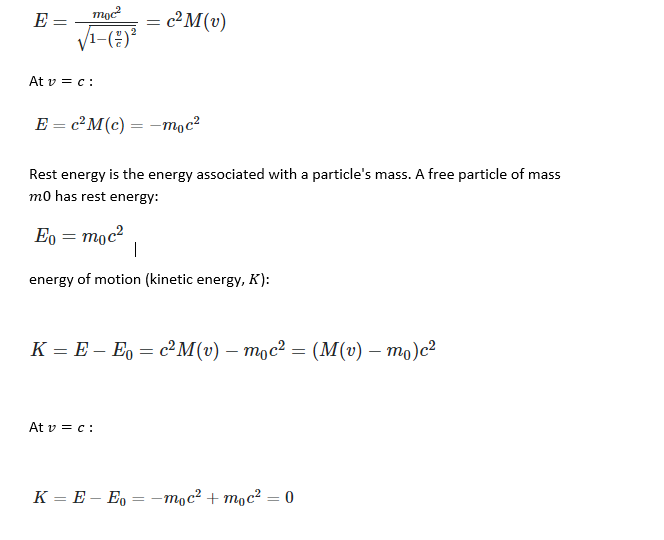
If we interpret its results, there may exist particles with a mass m0 and a negative relative mass -m0, having a negative total energy and a positive rest energy, along with zero kinetic energy. These particles could be generated by a physical phenomenon that accelerates particles with mass to the speed of light and could be linked to dark energy or dark matter.
3.Analogy of the theory with Casmir effect:
Here is an example of using regularization via the zeta function in the Casimir effect:
Mathematical calculations lead to the famous divergent series
1+2+3+4\ldotsHowever, the physical results do not correspond to infinite values for the energy of the moving plates.
To resolve this issue, we applied regularization through the Riemann zeta function. Eventually, we obtain a finite value of -1/12 for the divergent series1+2+3+4\ldots and this result provides a good explanation for the Casimir effect.
In analogy with the Casimir effect, it is possible that the value -M(0) obtained from the divergent series representing the relative mass at v=c,
U0+U1+U2+U3..., has a physical meaning to explain 95% of the missing energy in the universe.Hence, my hypothesis suggests the existence of a natural phenomenon that accelerates ordinary matter with mass to the speed of light and transforms it into dark matter or dark energy with negative relative mass and finite energy.
Could you please point out any possible errors in this new theory? The issue with the unit of measurement has been resolved.😀
-2 -
And here's another argument: at v=c, 1/(c-v)=1/(c-c)=1/0=infinity, and infinity has neither quantity nor unit of measurement. Therefore, I have no problem setting x+2=1/c-v.
0 -
To further support my argument, I give an example with f(x) and g(y), where f(x)=x and g(y)=1/y. I set f(x)=g(y), so I have x=1/y, which is true for any real x and y, even if I set y=0, and I get x=infinity. This equality remains valid even if x is no longer a number and equals infinity because I have infinity=1/0.
Next, with f(x) and g(v), where f(x)=x+2 and g(v)=1/(c-v). I set f(x)=g(v), so I have x+2=1/(c-v), which is true for any real x and v, even if I set v=c, and I get x+2=infinity. This equality remains valid even if x+2 is no longer a number and equals infinity because I have infinity=1/0. Therefore, at v=c, I have x+2=1/(c-v)=1/(c-c)=1/0=a/0, where c can have any unit, so x+2 does not have a unit of measurement.
I believe this argument is clear. If not, could you please point out any errors in this argument as well?
0 -
14 minutes ago, MJ kihara said:
Where did +2 come from....did you just fixed it to suit your arguments?
No, I didn't change 2 ,here we are discussing something else, we are talking about an equality and not a limit. And why does x+2 in this equality have no unit...😀
if they agree with my argument, we can move on to calculating the limit.😀
0 -
1 hour ago, joigus said:
Agreed. Not a language issue to me. Just plain wrong.
Dear @Z.10.46, there is a game in town that's very similar to what you're trying to play here. It's called asymptotics.
From: https://en.wikipedia.org/wiki/Asymptotic_analysis
In asymptotics we have to be very careful though. We never use the = sign. But we use an equivalence relation ≈ . If, eg, x is "very small", you're allowed to do things like (1+x)2≈1+2x , but never things like x≈0 , which lead to sorry mistakes. There is no such thing as "infinity" in asymptotics; only very big quantities, which must be either possitive or negative. Otherwise --like in your quite absurd, dimensionally inconsistent expression--, the "quantity" x defined by x+2=1/(c−v) with c=v is:
1) +infinity? That is, the right limit, or,
2) -infinity? That is, the left limit.
Of course infinity +2 = infinity, but also infinity + 3 = infinity, infinity +17=infinity-1/pi, etc.
And -infinity+2 = -infinity, etc. "Infinity" is not a number. It breaks all the algebraic rules. Example infinity + x = infinity + y does not imply x=y.
I like to think of infinity more like a topological entity (the boundary of the real numbers). I think that's the way in which modern mathematics we tend to look upon it. But that's another story.
And Swansont's objection about units still stands.
Yes, I know that. I didn't write x+1~x or x^3+x^2+x+1x^3~x^3.
I wrote x+2=1/c-v=1/c-c. You notice that I have two different notations, x and c.
Why am I choosing ~?
It's like saying I have f(x)=g(y)=1/c-c=1/0=a*1/0 with a in R+*.
 1 hour ago, swansont said:
1 hour ago, swansont said:If v=c you do not have a valid equation
1/c-v is a function, valid for v≠c. If you choose v=c (or any fixed value) you do not have a function.
You can do one or the other. Not both.
Functions are not equal simply because they both diverge to the same limit.
x and x+2 both go to infinity, but x ≠ x+2
Is it true that 1/(c-v) = 1/(c-c) = 1/0 = a*1/0 with a in R*+ when v=c?
If it is true, then I would set x+2=1/c-c=1/0=a/0 with a>0. Therefore, x+2 would not have any unit because even if I change the value of c, I would still have x+2=1/c-c=1/0=a/0, and thus x+2 would not have any unit.
0 -
29 minutes ago, swansont said:
1/c-v is not infinite; you can graph it and see that it tends to infinity as v approaches c, but you wrote is as a function. x+2 is not infinite either. You can’t arbitrarily set them equal to each other, and can’t use them as equations where x and v are variables, because you aren’t treating them as variables.
It also looks like you are saying that two functions that tend to infinity in some limit are equal, which is just wrong.
Here, I am not just saying that v tends to c, I am saying that v=c, so 1/c-v egal infinity not just tends to infinity , if I set x+2=1/c-v, it's like having the equality infinity+2=infinity
I agree with you that it is impossible to do this for a finite quantity but 1/c-v is not finite at v=c and in this case setting x+2=1/c-v is valid without a fixed unit as I demonstrated.
0 -
54 minutes ago, joigus said:
My Dunning-Kruger effect sensor went off the scale here.

Your handling of units and zero/infinity is appaling.
Yes, but it's a very solid mathematical proof to justify that x+2 has no unit because the equation x+2=1/c-v is true for any unit of measurement chosen for c, due to the property that infinity=a*infinity, similar to the '1' in the equation 1=c/c which has no unit of measurement as this equation is true for any unit of measurement chosen for c.😁
16 minutes ago, swansont said:Which isn’t a language issue; the math is just flat-out wrong.
Could you point out a possible error in this proof?
0 -
6 minutes ago, MJ kihara said:
Clarification pliz line 3 to line 4 where is denominator c^2 going?
1. M = m0 / √(1 - v^2/c^2) =
2. = m0 / √(c^2 - v^2)/c^2 =
3. = m0 / √(c + v)√(c - v)/c^2 =
Here 1/√1/c^2=c
4. = m0c / √(c + v)√(c - v) =
here c+v=c+c To isolate the divergence (c - v).
6. = m0c / √(c + c)√(c - v) =
7. = m0c / √2c√(c - v) =
8. = m0√c / √2√(c - v) =
9. = m0√c / √2√n
0 -
20 minutes ago, studiot said:
You have shown it to this Mathematician.
And I thought there were too many misunderstndings in it to be worth detailed consideration.
So +1 to Genady for the patience to do this.
+1 also to PhiforAll who got in before me when I was about to complain.
A word of advice.
You can expect ridicule as answers when you make such wildly and obviously incorrect statements.
Such as claiming the non existence of zero.
Consider this sequence of integers
...-4, -3, -2, -1, 1, 2, 3, 4...
...Even, odd, even, odd, odd, even, odd, even...
Do you notice anything missing ?
It implies that there are more odd numbers than even numbers.
By the way do you understand the ... symbol?
It is called an ellipsis.
You have also been arguing wrongly about the meaning of the equals sign.
It stands for two different properties - Identity, and simple equality.
Sometimes the identity symbol with three bars not two is used instead for this.
It seems like you are searching for errors where there is no ,mathematical demonstration that is 100% correct.
In this discussion, those who understand mathematics and physics very well have highlighted the only flaw in this proof, which is to assume x+2=1/c-v without considering the unit of c.
However, the counterproof was very strong because the relationship remains valid regardless of the unit of c, just like the equation c/c=1, which is always true regardless of the unit of c.
The discussion about the non-existence of 0 in physics is just off-topic. Here, you are talking about mathematical zero, while I am talking about the non-existence of a physical zero.
-2 -
12 minutes ago, Genady said:
Yes, there is an error.
After you set c=v on line 5, you get m0c/0 on line 6. Anything after that is meaningless, because there is no such thing as dividing by 0.
I haven't done it. The purpose of this is to let the divergence appear in order to apply regularization using the zeta function.
in other words, Md is a simplification of M in the vicinity of v=c that is equivalent.
0 -
8 minutes ago, Genady said:
I've asked a mathematician and he wanted to clarify, if this is what you are saying:
1. M = m0 / √(1 - v^2/c^2) =
2. = m0 / √(c^2 - v^2)/c^2 =
3. = m0 / √(c + v)√(c - v)/c^2 =
4. = m0c / √(c + v)√(c - v) =
5. = √(c + c)√(c - v) =
6. = m0c / √(c + c)√(c - v) =
7. = m0c / √2c√(c - v) =
8. = m0√c / √2√(c - v) =
9. = m0√c / √2√n
?
1. M = m0 / √(1 - v^2/c^2) =
2. = m0 / √(c^2 - v^2)/c^2 =
3. = m0 / √(c + v)√(c - v)/c^2 =
4. = m0c / √(c + v)√(c - v) =
5.c=v so (c+v)=c+c=2c
6. = m0c / √(c + c)√(c - v) =
7. = m0c / √2c√(c - v) =
8. = m0√c / √2√(c - v) =
9. = m0√c / √2√n
0 -
5 minutes ago, Genady said:
I don't think your mathematical calculation is correct. To make it readable, break it down line by line. Then I think you will see an error.
no it's correct you can show it to any mathematician, I'm not going to give a theory either where there is a calculation error and without verification by mathematicians😁
And the journal wouldn't have offered me the possibility to publish this theory if it were mathematically invalid.😄
13 minutes ago, MJ kihara said:Where there is smoke...their is fire ....keep following the smoke...when did you start developing this concept?
several years I thought about this idea but I just reformulated it mathematically less than a year ago thanks to the help of online mathematicians.
0 -
7 minutes ago, Genady said:
It is a mathematical calculation for example:
M = m0 / √(1 - v^2/c^2) ~ m0 / √(c^2 - v^2)/c^2 ~ m0 / √(c + v)√(c - v)/c^2 ~ m0c / √(c + v)√(c - v)=√(c + c)√(c - v) ~ m0c / √(c + c)√(c - v) ~ m0c / √2c√(c - v) ~ m0√c / √2√(c - v)~ m0√c / √2√n
0 -
29 minutes ago, Bufofrog said:
I see part of the problem. In the above you did not change the units.
The units are m/s, the exponents are 8 and 5.
Go ahead, you can choose any unit for c. Does the relationship remain true even if I change the unit for c?😁
If the relationship is true for any unit of c, that means it does not depend on the unit of c to pose x+2=1/c-v at v=c and x tends to infinity .😀
Why we say, for example in this equation 1=c/c, it does not depend on any unit of c, is because regardless of the chosen unit, you always obtain 1. Similarly, here in the equation x+2=1/(c-v), when c=v and x tends to infinity, this relationship holds true. Hence, it does not depend on any unit of c, just like c/c=1.😇
0 -
30 minutes ago, Phi for All said:!
Remarque du modérateur
Non. Ils n'ont pas les mêmes unités.
Vous avez eu 5 pages pour nous persuader que votre idée a du mérite, et ce n'est pas la première erreur que vous commettez. Vous n'arriverez à convaincre personne que si vous faites preuve de plus de rigueur dans vos explications. Si vous ne pouvez pas le faire, nous devrons fermer ce fil.
The problem with units is that if I change them, for example, to (c-1), I will obtain a different value each time. But here, when I state x+2=1/c-v, it poses no problem because regardless of the unit of c, this formula x+2=1/c-v will always hold true since infinity=infinity=a*infinity. Here's an example, let c=3.10^8 m/s, and I have x+2=1/c-v. Now, if I change the unit to c=3.10^5 m/s or any other unit, I will still have this relation true, x+2=1/c-v. Thus, this relationship does not depend on any unit of measurement as it is an equation involving divergences or infinity=infinity=a*infinity, unlike (c-1) where its value changes depending on the unit of c And it depends on the unit of c that I choose.
Here is a very solid proof to set x+2=1/c-v because this equality relationship between infinities does not depend on any unit of c, it is true for any unit of c.
.
.
0 -
1 hour ago, swansont said:
Cela ne fonctionne pas ainsi.
L'idée que vous pouvez multiplier un côté de l'équation par un facteur et penser que cela reste une égalité souligne à quel point cette affirmation est ridicule.
I don't see anything ridiculous about x+2=1/c-v, as x, 2, and 1/c-v all have the same unit. Even if I write x+a=1/c-v, I still obtain M(c)=-M(c-1), even if the unit of c changes. So, regardless of the units used, it doesn't pose any problem, and I always get M(c)=-M(c-1).
In essence, x+a=1/c-v is valid for any value of a, so even if the unit of c changes, it doesn't pose any problem because it corresponds to a specific value of a where this equality is always true x+a=x+2=1/c-v at v=c .
here exemple c=3^10^8 and c=1 x+2=1/c-v with x et 2 and 1/c-v have the same unit is true.😁 becouse infinty=infinity=a*infinity=infinity+a 😁
-1 -
(x+2) and 1/c-v have the same units because I've established an equality.
I can even set x+2/c=1/(c-v) and I will still have M(c)=M(c-1)
0 -
-
16 minutes ago, Genady said:
However, there is no such problem in this case. YOU make the problem up.
and why not do it since it is possible to open up new avenues in theoretical physics.?
0

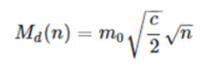

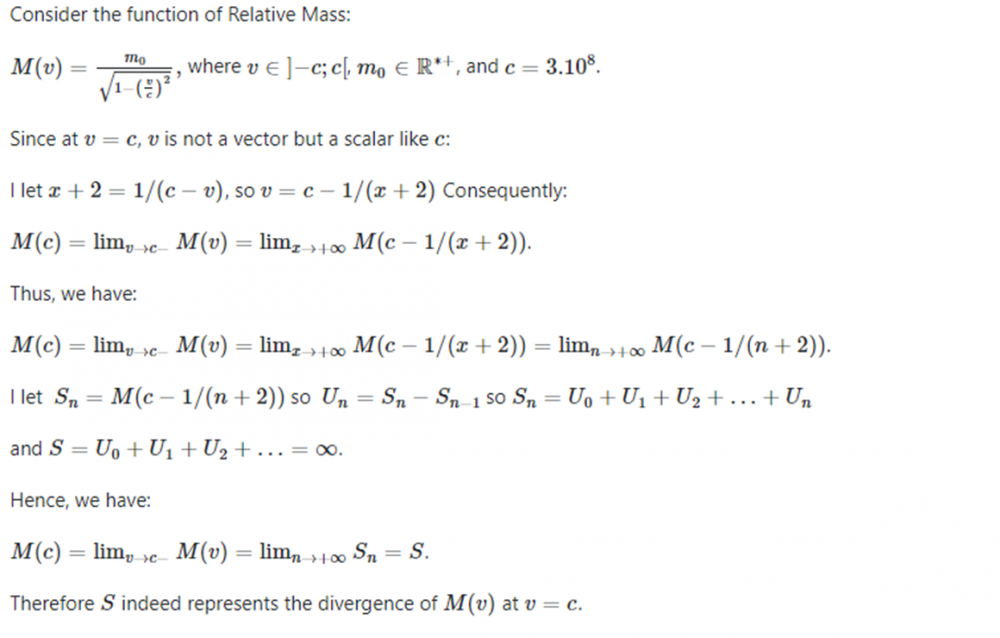
Proof that twin primes are infinite.
in Applied Mathematics
Posted · Edited by Z.10.46
For your information, even if 'a' and 'b' tend towards infinity, they would still be negligible compared to the infinity of 'n/ln(n)' and 'n+2/ln(n+2)', similar to, for example, 'n' or '-n' being negligible compared to 'n^2'. That's why the ratio π(x)/(x/ln(x)) tends towards 1, even as 'a' and 'b' tend towards infinity.
To be more mathematically rigorous, I choose 'a' and 'b' as sequences 'a_k' and 'b_k' with 'n/ln(n)+a_k = N' and '(n+2)/ln(n+2)+b_k = N+1', so '1+n/ln(n)+a_k = (n+2)/ln(n+2)+b_k' Even as 'a_k' and 'b_k' tend towards infinity, the equation remains true, thus indicating the existence of an infinite number of twin prime numbers. If there were not an infinite of twin prime numbers,This equation would admit only one solution for a specific small value of 'n'.