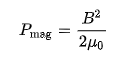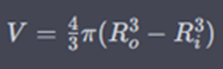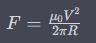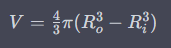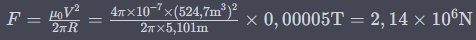Kassander

Wow, thanks’ a lot! This seems to be the answer why a type-I superconductor would never get enough uplift for any of my suggested usages. Exchemist gave me another formula yesterday and we also calculated a very small uplift of 0,5kg. But we were not sure if the formulas we used where appropriate in this case. Anyway, it seems to stabilize that an extension of the volume is not enough to increase the uplift capacity to a useful amount. So the only remaining question is if a flux pinned type-II superconductor would also not provide enough uplift in earth’s magnetic field for a practical usage. Or is the flux pinning-effect already part of your calculations? To be honest, I don´t understand every part of what you have calculated 😉. But I think ChatGPT had used the flux pinning-effect in his calculation. It choose the Niobium–titanium (Nb-Ti) superconductor probably because this is a type-II superconductor. According to all online sources I can find the flux pinning get stronger when the superconducting layer gets thinner. But I can´t find any formula for that. “I would think the relevant dimension of the superconductor is the area it presents to the magnetic field.” Since the volume is part of the equation the area should be considered. Anyway, TheVat calculated the lift capacity in detail. The result is pretty close to the 0,5kg. So increasing the volume and using a hollow superconductor is not the solution to get enough lift capacity in earth’s magnetic field for practical usage. The only remaining question is if the flux pinning-effect also not provides a significant increase in lift capacity. But I think we can assume that this is the case because we would see for sure many technical uses if this would be possible.

“How do you get this?” Here again the calculation of the magnetic pressure in pascal according to the formula: (0.00005²T)/(2(4π*(10^-7))) = 0.0009947Pa “How come B is in N?” There are two “B”. The first one seen in the formula for magnetic pressure is not in n Newton but in Tesla. So I filled in 0.00005T for earth’s magnetic field. The second “B” in the formula to calculate the buoyancy stands for buoyancy. Buoyancy is of course a force and that’s why it´s in “N” for Newton. “How do you get this?” Exactly as I said, I filled in p=0.0009947Pa and V=523.599m³ in this online calculator: https://www.omnicalculator.com/physics/buoyancy This calculator give than the mentioned result´s out B=5.108N and a Mass of displaced fluid of 0.5208kg. “What fluid?” The mentioned online calculator is made for buoyancy calculations in water. That´s why the programmer called it “Mass of displaced fluid”. However I think it would be proper to use this for our calculation.

Thank you for your answer. I´m not good at the usage of formulas. The same goes for the conversion of units. But according to the following Wiki-Article, which was previously linked by exchemist and was the base of my calculation, the result should be in pascals: https://en.wikipedia.org/wiki/Magnetic_levitation To avoid any further mistakes, I now used this online calculator: https://www.omnicalculator.com/physics/buoyancy When I now fill in p=0.0009947Pa and V=523.599m³ I get B=5.108N and a Mass of displaced fluid of 0.5208kg. Which is what I calculated bevor. Or got I something wrong?

The formula for the magnetic pressure you asked me to calculate gave out 0.0009947Pa. Pa or Pascal is the unit for pressure. If you multiply it with the volume of any object and g you should get the buoyancy/upthrust, not just in liquid water but in general I assume. Was not that what you wanted to know?

I also think it would be better if we try to do it ourselves. I have asked ChatGPT multiple times, and this is the only useful answer I have received: Here is the link to the Wikipedia article on the London Equations: https://en.wikipedia.org/wiki/London_equations When I input the numbers for Earth's magnetic field into the formula from your link, this is what I get: (0.00005²T)/(2(4π*(10^-7))) = 0.0009947Pa Now, when I use the formula for buoyancy in liquid water, I get: B = pVg | 0.0009947Pa * 523.599m³ * 9.81 = 5.11N 5.11N is a very low number - you could lift just about 0.5 kg, and the weight of the construction has not yet been subtracted. So this may be the reason why no one uses this concept, if the calculation is correct. However, I am not sure if it is appropriate to use the formula for buoyancy in liquid water in this particular case. ChatGPT mentioned the London Equations, which are also related to the Meissner–Ochsenfeld Effect: https://en.wikipedia.org/wiki/Meissner_effect I also think that ChatGPT chose a Niobium-Titanium (Nb-Ti) superconductor because it is a Type-II superconductor, which can be used for "flux pinning", this would generate a much greater force than just the magnetic levitation, but no formulas are mentioned: https://en.wikipedia.org/wiki/Flux_pinning I believe that with this Wikipedia article, I have found the key to what I was previously looking for. It mentions that “the ability to fix the superconductor in space can be used as a damping device, like a spring. This idea has been proposed for isolating vibrations for parts in satellites.” This is a pretty similar idea to my suggestion of using it in a spacecraft for deceleration. No, an AI is not necessarily necessary. I think we are already close to a solution at this point.

Sorry for my late reply. During my first few days, I could only post five comments per day, so I had to wait. Before his last calculation, ChatGPT wrote, "The magnetic field strength of Earth's magnetic field is about 0.5 Gauss or 0.00005 Tesla." He correctly included this value of 0.00005T as he multiplied it with the formula. However, I am not sure if he calculated the formula correctly afterwards. I obtained a very small number when I used my calculator, but it's possible that I made a mistake when converting the units. Sorry, I could not answer earlier because I can only publish five comments a day since I signed up yesterday. I told ChatGPT that it made a mistake in the calculation and it figured out the problem without any help. That is what it wrote: But I have found another problem. When I calculate the formula, the result is (((4π*(10^-7))(523.91)²)/(2π5.01))0.00005 = 5.4786810^-7. This is a very small number, but I am not sure if it needs to be converted to another unit. If a conversion is necessary, it may explain how ChatGPT calculated 209t. However, when I asked for an explanation, I received answers with more mistakes. As far as I can see, these answers are completely useless: According to ChatGPT 1mm should be enough to keep magnetic fields out. I discussed this with him before the calculation and he wrote: ChatGPT: The thickness of the superconducting layer depends on various factors, such as the specific superconducting material composition and the desired levitation parameters. A rough estimate could be made based on the critical current density of the superconducting material. For example, if we take niobium-titanium (NbTi) as the superconducting material and assume a critical current density of 100 A/mm², then a required area of about 0.01 m² is obtained for a load of 1000 kg. From this, an approximate thickness of the layer can be calculated by dividing the volume of the required material by the required area. For a layer thickness of 1 µm, for example, a required volume of 10^-11 m³ is obtained. With a layer thickness of 10 µm, the required volume increases to 10^-10 m³. However, these values are only rough estimates and can vary significantly depending on the specific circumstances. Me: So, if we take a 1mm thick layer, are we on the safe side? ChatGPT: A 1mm thick layer should be sufficient to ensure the superconductivity of the material and enable sufficient load capacity. However, the actual thickness of the layer also depends on other factors, such as the type of material and application. Therefore, it may be useful to conduct further investigations to determine the optimal layer thickness for a specific application. I asked him again and he wrote:

Ah, okay, so this would be the correct calculation: First, we need to calculate the volume of the wall of the sphere using the formula that ChatGPT provided but did not calculate. The calculation would be: ((3/4)π)((5+0.01)³-(5-0.1)³=19.09m³ So the volume of the wall of the sphere is V1=19.09m³. Next, we need to calculate a second volume to use in the formula that calculates the force. For this, we need the entire space enclosed by the superconductor, which has a radius of 5.01m. According to an online calculator, the result of this calculation is 523.91m³. This is slightly less than the 524.7m³ that ChatGPT calculated, and the 523.3m³ that you calculated, so it seems to be fairly accurate. Thus, we have V2=523.91m³. So we need to use V2=523.91m³ instead of 524.7m³ and a radius of 5.01m instead of 5.101m in the formula for the force. But would this change really make that much of a difference?

ChatGPT has calculated a volume of 524.7m³, which is exactly the same as the volume calculated by an online calculator for a sphere with a radius of 5m. In the last formula ChatGPT used 5.101m to put this in for the Radius witch is also correct. The last formula should calculate the force required to hold the payload. Therefore, there is no need to calculate the volume of the sphere's wall. In the final sentence, ChatGPT states that after subtracting the weight of the superconductor, a payload of 209t can be calculated. To know the weight of the superconductor it´s necessary to know the volume of the sphere's wall. However, ChatGPT has not shown the calculation for the volume of the wall. I don´t get where are you seeing the 20cm thickness and volume of 62.8 m^2?

I have also noticed that, which is why I am now asking here 😉.

Yes, in the case of the first possible usage, that could certainly pose a major problem. However, the other two would likely only be restricted by it. But I hadn't thought of that, thank you for the response!

First of all, sorry for my bad English, I am from Austria, so it's not my mother tongue. I know that an ordinary superconductor could not levitate in Earth's magnetic field because its weight is higher than the force that Earth's magnetic field can carry. But the simple solution is to use superconductors that are hollow inside. This would drastically reduce their weight without reducing their lifting capacity. Even smarter would be to cover a light and solid material with a thin layer or foil of some superconducting material. To increase the stability of the object even more, you can choose a stable structure like a sphere and use struts in an optimized way. This would reduce the weight even more because less material would be needed to keep the structure stable. I asked ChatGPT how much a hollow sphere with a diameter of 10m and wall thickness of 10cm that is covered with a 1mm layer of superconducting Nb-Ti could carry in Earth's magnetic field. This was its answer: “The load capacity of a hollow aluminum sphere with a shell thickness of 10cm and a 1mm thick superconducting niobium-titanium layer in Earth's magnetic field can be calculated using the following formula: where F is the maximum load capacity of the superconductor, μ_0 is the magnetic field constant, V is the volume of the superconductor, and R is the radius of the superconductor. The volume of the hollow aluminum sphere with an outer radius of 5m and a wall thickness of 10cm can be calculated as follows: where R_o is the outer radius and R_i is the inner radius of the sphere. Thus, we get: Therefore, the radius of the superconductor is R = 5m + 0.1m + 0.001m = 5.101m. The magnetic field strength of Earth's magnetic field is about 0.5 Gauss or 0.00005 Tesla. The maximum load capacity of the superconductor can thus be calculated as: Subtracting the weight of the superconductor, the maximum payload is about 209 tons.” Since I cannot calculate this on my own, I cannot say if this is correct, but if it is, this would be a highly energy-efficient way to transport things since you don't need energy to hold the payload up. Due to the Meissner-Ochsenfeld effect, the object would be locked in the magnetic field lines. I know you could not use the full capacity of 209 metric tonnes because you need an isolation layer and a cooling system, but there would still be a lot of payload capacity available. A second possible use of this technique would be to reach space with it. Normally, you are locked in the magnetic field lines due to the Meissner-Ochsenfeld effect. However, if you use two or more spheres and switch the superconductivity on and off, you can climb up to space like a gecko. It sounds strange and would look strange for sure, but if the calculations are correct, it would be absolutely possible. Of course, you would not have escape velocity or even enough velocity to reach an orbit, but for cheap and safe space tourism, this would be enough. A third possible use would be to reduce costs and risks in the re-entry phase of every space-flying object. To decelerate from the high velocities needed for spaceflight, a huge amount of energy is needed. Heat shields such as those seen on the Space Shuttle or Starship are expensive and a huge risk factor in space travel. Due to the Meissner-Ochsenfeld effect, a smaller version of the calculated sphere would decelerate every spacecraft in the re-entry phase. It has to be calculated whether the amount of energy saved because of the deceleration is higher than the amount of energy needed to bring this structure in the spacecraft up to space. But since the enormous amount of energy needed to break through the magnetic field lines when a superconducting object is locked, I'm optimistic that there would be a positive outcome. In the future, when space mining and space manufacturing become topics, this could possibly save a lot of energy and money in bringing goods back to Earth. So there are three possible ways to use this technology. But why is no one developing it? Or is there something wrong with ChatGPT's calculation?