xyrth

I corrected the comparison about the factor (t1-t0) and (t1-t0)², the text in red color. I'm looking for another mistake.

 

No external gravity. No friction. No external motor.

 

 

Rotational velocity of the disk at start: w0

The distance of the center of mass of the screw-thread from the center of the disk at start: d

The mass of the screw-thread: m

The mass of the disk: md = 0

Radius of the screw-thread: R

The inertia of the thread in its main own axis (when the thread rotates around itself) : Ir

The inertia of the thread in axis y: Iy

At start, time t = 0 s

The force of the device composed of several springs is constant: F

 

The center of mass of the screw-thread moves away the center of the disk at the speed √3/2*2πR for each turn of the screw-thread on the disk. The rotational velocity of the screw-thread relatively to the disk is w(t)*cos(30°). So, the center of mass moves at v(t)=√3/2*2πR*w(t)*cos(30°)/2/π = √3/2*R*w(t)*cos(30°) = 3/4*R*w(t)

Like there is no external motor the rotational velocity of the disk is a function of time: w(t)=d/(d+v(t)*t)*w0

The screw-thread is turning at ws(t)=√3/2*w(t) on the disk

 

When I attach at time ‘t0’ the spring the angular velocities are changed and I need to take in accound the inertia of the screw-thread. At time = t1, I stop to count the energies.

 

With the spring the angular velocity of the disk is changed:

wr(t)=w(t)-(√3/2+1/2)RF/Ir*(t-t0)

 

For a delta time t1-t0, the angle is :

 

wr(t)*(t1-t0)

= (w(t)-(√3/2+1/2)RF/Ir*(t1-t0) ) * (t1-t0)

 

The major part of the angle is changed by w(t) * (t1-t0) not by (√3/2+1/2)RF/Ir*(t1-t0)²

 

And the angular velocity of the thread is also changed by the spring in:

wsr(t)=√3/2*wr(t)-1/2*RF/Iy*(t-t0)

 

For a delta time t1-t0, the angle is :

 

wsr(t)*(t1-t0)

= (√3/2*wr(t)-1/2*RF/Iy*(t1-t0)) * (t1-t0)

 

The major part of the angle is changed by wr(t)* (t1-t0) not by 1/2*RF/Iy*(t1-t0)²

 

The energy won by the spring is :

 

+(wsr(t1)+wrs(t0))/2*(t1-t0)*2*RF

= +( √3/2*wr(t1)-1/2*RF/Iy*(t1-t0) + √3/2*wr(t0)-1/2*RF/Iy*(t0-t0) ) /2 *(t1-t0) *2*RF

= +( √3/2*(w(t1)-(√3/2+1/2)RF/Ir*(t1-t0))-1/2*RF/Iy*(t1-t0) + √3/2*(w(t0)-(√3/2+1/2)RF/Ir*(t0-t0))-1/2*RF/Iy*(t0-t0) ) /2 *(t1-t0) *2*RF

 

The energy lost from the torque of the force F on the disk, at distance R from the center of the disk is :

 

-(wr(t1)+wr(t0))/2*(t1-t0)*√3/2*RF

= -(w(t1)-(√3/2+1/2)RF/Ir*(t1-t0)+w(t0)-(√3/2+1/2)RF/Ir*(t0-t0))/2*(t1-t0)*√3/2*RF

 

The energy lost from the force F on the axis ‘y’ on the disk is:

 

-(wr(t1)+wr(t0))/2*(t1-t0)*1/2*RF
= -(w(t1)-(√3/2+1/2)RF/Ir*(t1-t0) + w(t0)-(√3/2+1/2)RF/Ir*(t0-t0) )/2*(t1-t0)*1/2*RF

 

 

The energy lost by the center of mass is:

 

 -3/4*RF*(wsr(t1)+wsr(t0))/2*(t1-t0)

=  -3/4*RF*(√3/2*wr(t1)-1/2*RF/Iy*(t1-t0) + √3/2*wr(t0)-1/2*RF/Iy*(t0-t0))/2*(t1-t0)

= -3/4*RF*(√3/2*(w(t1)-(√3/2+1/2)RF/Ir*(t1-t0))-1/2*RF/Iy*(t1-t0) + √3/2*(w(t0)-(√3/2+1/2)RF/Ir*(t0-t0))-1/2*RF/Iy*(t0-t0))/2*(t1-t0)

 

 

For a small angle from the time t0 I attached the spring, (t1-t0) near equal to 0 but -(√3/2+1/2)RF/Ir*(t1-t0)² is near 0 at square and for -1/2*RF/Iy*(t1-t0)² it is the same, I can approximate the sum of energy. For example if t1-t0=0.01 then (t1-t0)²=0.0001.

 

 

The sum of energy is well at:

 

- 0.28*RF*(t1-t0)*(wr(t1)+wr(t0))/2

 

In fact, it is logical because the angular velocity for the disk is w(t)=w0-k*t with 'k' a constant and the angle of rotation is w(t)*t = (w0-k*t)*t and if t is small the factor kt² is negligible. So, one work I calculated is wrong.

28 minutes ago, Strange said:

Perhaps you need to think of some way of checking each step of your calculation individually to find the error. (You do know there is an error, yes?)

It is what I'm doing, I found a little mistake but it is more for the expression of the angular velocity of the disk due to the movement of the center of mass:

 

No external gravity. No friction. No external motor.

 

 

Rotational velocity of the disk at start: w0

The distance of the center of mass of the screw-thread from the center of the disk at start: d

The mass of the screw-thread: m

The mass of the disk: md = 0

Radius of the screw-thread: R

The inertia of the thread in its main own axis (when the thread rotates around itself) : Ir

The inertia of the thread in axis y: Iy

At start, time t = 0 s

The force of the device composed of several springs is constant: F

 

The center of mass of the screw-thread moves away the center of the disk at the speed √3/2*2πR for each turn of the screw-thread on the disk. The rotational velocity of the screw-thread relatively to the disk is w(t)*cos(30°). So, the center of mass moves at v(t)=√3/2*2πR*w(t)*cos(30°)/2/π = √3/2*R*w(t)*cos(30°) = 3/4*R*w(t)

Like there is no external motor the rotational velocity of the disk is a function of time: w(t)=d/(d+v(t)*t)*w0

The screw-thread is turning at ws(t)=√3/2*w(t) on the disk

 

When I attach at time ‘t0’ the spring the angular velocities are changed and I need to take in accound the inertia of the screw-thread. At time = t1, I stop to count the energies.

 

With the spring the angular velocity of the disk is changed:

wr(t)=w(t)-(√3/2+1/2)RF/Ir*(t-t0)

 

For a delta time t1-t0, the angle is :

 

wr(t)*(t1-t0)

= (w(t)-(√3/2+1/2)RF/Ir*(t1-t0) ) * (t1-t0)

 

The major part of the angle is changed by w(t) * (t1-t0) not by (√3/2+1/2)RF/Ir*(t1-t0)²

 

And the angular velocity of the thread is also changed by the spring in:

wsr(t)=√3/2*wr(t)-1/2*RF/Iy*(t-t0)

 

For a delta time t1-t0, the angle is :

 

wsr(t)*(t1-t0)

= (√3/2*wr(t)-1/2*RF/Iy*(t1-t0)) * (t1-t0)

 

The major part of the angle is changed by wr(t)* (t1-t0) not by 1/2*RF/Iy*(t1-t0)²

 

The energy won by the spring is :

 

+(wsr(t1)+wrs(t0))/2*(t1-t0)*2*RF

= +( √3/2*wr(t1)-1/2*RF/Iy*(t1-t0) + √3/2*wr(t0)-1/2*RF/Iy*(t0-t0) ) /2 *(t1-t0) *2*RF

= +( √3/2*(w(t1)-(√3/2+1/2)RF/Ir*(t1-t0))-1/2*RF/Iy*(t1-t0) + √3/2*(w(t0)-(√3/2+1/2)RF/Ir*(t0-t0))-1/2*RF/Iy*(t0-t0) ) /2 *(t1-t0) *2*RF

 

The energy lost from the torque of the force F on the disk, at distance R from the center of the disk is :

 

-(wr(t1)+wr(t0))/2*(t1-t0)*√3/2*RF

= -(w(t1)-(√3/2+1/2)RF/Ir*(t1-t0)+w(t0)-(√3/2+1/2)RF/Ir*(t0-t0))/2*(t1-t0)*√3/2*RF

 

The energy lost from the force F on the axis ‘y’ on the disk is:

 

-(wr(t1)+wr(t0))/2*(t1-t0)*1/2*RF
= -(w(t1)-(√3/2+1/2)RF/Ir*(t1-t0) + w(t0)-(√3/2+1/2)RF/Ir*(t0-t0) )/2*(t1-t0)*1/2*RF

 

 

The energy lost by the center of mass is:

 

 -3/4*RF*(wsr(t1)+wsr(t0))/2*(t1-t0)

=  -3/4*RF*(√3/2*wr(t1)-1/2*RF/Iy*(t1-t0) + √3/2*wr(t0)-1/2*RF/Iy*(t0-t0))/2*(t1-t0)

= -3/4*RF*(√3/2*(w(t1)-(√3/2+1/2)RF/Ir*(t1-t0))-1/2*RF/Iy*(t1-t0) + √3/2*(w(t0)-(√3/2+1/2)RF/Ir*(t0-t0))-1/2*RF/Iy*(t0-t0))/2*(t1-t0)

 

 

For a small angle from the time t0 I attached the spring, (t1-t0) near equal to 0 but -(√3/2+1/2)RF/Ir*(t1-t0)² is 10 times smaller and -1/2*RF/Iy*(t1-t0)² is 10 times smaller, I can approximate the sum of energy.

 

 

The sum of energy is well at:

 

- 0.28*RF*(t1-t0)*(wr(t1)+wr(t0))/2

No external gravity. No friction. No external motor.

 

 

Rotational velocity of the disk at start: w0

The distance of the center of mass of the screw-thread from the center of the disk at start: d

The mass of the screw-thread: m

The mass of the disk: md = 0

Radius of the screw-thread: R

The inertia of the thread in its main own axis (when the thread rotates around itself) : Ir

The inertia of the thread in axis y: Iy

At start, time t = 0 s

The force of the device composed of several springs is constant: F

 

The center of mass of the screw-thread moves away the center of the disk at the speed √3/2*2πR for each turn of the screw-thread on the disk. The rotational velocity of the screw-thread relatively to the disk is w(t)*cos(30°). So, the center of mass moves at v(t)=√3/2*2πR*w(t)*cos(30°)/2/π = √3/2*R*w(t)*cos(30°) = 3/4*R*w(t)

Like there is no external motor the rotational velocity of the disk is a function of time: w(t)=w0-d/(d+v(t)*t)

So the screw-thread is turning at ws(t)=√3/2*w(t) on the disk

 

When I attach at time ‘t0’ the spring the angular velocities are changed and I need to take in accound the inertia of the screw-thread. At time = t1, I stop to count the energies.

 

With the spring the angular velocity of the disk is changed:

wr(t)=w(t)-(√3/2+1/2)RF/Ir*(t-t0)

 

For a delta time t1-t0, the angle is :

 

wr(t)*(t1-t0)

= (w(t)-(√3/2+1/2)RF/Ir*(t1-t0) ) * (t1-t0)

 

The major part of the angle is changed by w(t) not by (√3/2+1/2)RF/Ir*(t-t0)

 

And the angular velocity of the thread is also changed by the spring in:

wsr(t)=√3/2*wr(t)-1/2*RF/Iy*(t-t0)

 

For a delta time t1-t0, the angle is :

 

wsr(t)*(t1-t0)

= (√3/2*wr(t)-1/2*RF/Iy*(t1-t0)) * (t1-t0)

 

The major part of the angle is changed by wr(t) not by 1/2*RF/Iy*(t-t0)

 

The energy won by the spring is :

 

+(wsr(t1)+wrs(t0))/2*(t1-t0)*2*RF

= +( √3/2*wr(t1)-1/2*RF/Iy*(t1-t0) + √3/2*wr(t0)-1/2*RF/Iy*(t0-t0) ) /2 *(t1-t0) *2*RF

= +( √3/2*(w(t1)-(√3/2+1/2)RF/Ir*(t1-t0))-1/2*RF/Iy*(t1-t0) + √3/2*(w(t0)-(√3/2+1/2)RF/Ir*(t0-t0))-1/2*RF/Iy*(t0-t0) ) /2 *(t1-t0) *2*RF

 

The energy lost from the torque of the force F on the disk, at distance R from the center of the disk is :

 

-(wr(t1)+wr(t0))/2*(t1-t0)*√3/2*RF

= -(w(t1)-(√3/2+1/2)RF/Ir*(t1-t0)+w(t0)-(√3/2+1/2)RF/Ir*(t0-t0))/2*(t1-t0)*√3/2*RF

 

The energy lost from the force F on the axis ‘y’ on the disk is:

 

-(wr(t1)+wr(t0))/2*(t1-t0)*1/2*RF
= -(w(t1)-(√3/2+1/2)RF/Ir*(t1-t0) + w(t0)-(√3/2+1/2)RF/Ir*(t0-t0) )/2*(t1-t0)*1/2*RF

 

 

The energy lost by the center of mass is:

 

 -3/4*RF*(wsr(t1)+wsr(t0))/2*(t1-t0)

=  -3/4*RF*(√3/2*wr(t1)-1/2*RF/Iy*(t1-t0) + √3/2*wr(t0)-1/2*RF/Iy*(t0-t0))/2*(t1-t0)

= -3/4*RF*(√3/2*(w(t1)-(√3/2+1/2)RF/Ir*(t1-t0))-1/2*RF/Iy*(t1-t0) + √3/2*(w(t0)-(√3/2+1/2)RF/Ir*(t0-t0))-1/2*RF/Iy*(t0-t0))/2*(t1-t0)

 

 

For a small angle from the time t0 I attached the spring, (t1-t0) near equal to 0 but -(√3/2+1/2)RF/Ir*(t1-t0)² is 10 times smaller and -1/2*RF/Iy*(t1-t0)² is 10 times smaller too, the energies are counted from t0 to t1, the energies are:

 

 

The sum of energy is well at:

 

- 0.28*RF*(t1-t0)*(wr(t1)+wr(t0))/2

 

Ok, I done calculations without any motor.

 

No external gravity. No friction. No external motor.
Rotational velocity of the disk at start: w0
The distance of the center of mass of the screw-thread from the center of the disk at start: d
The mass of the screw-thread: m
The mass of the disk: md = 0
Radius of the screw-thread: R
The inertia of the thread in its main own axis (when the thread rotates around itself) : Ir
The inertia of the thread in axis y: Iy
At start, time t = 0 s
The force of the device (I drew a spring but it is a composition of springs) composed of several springs is constant: F

The center of mass of the screw-thread moves away the center of the disk at the speed √3/2*2πR for each turn of the screw-thread on the disk. The rotational velocity of the screw-thread relatively to the disk is w(t)*cos(30°). So, the center of mass moves at v(t)=√3/2*2πR*w(t)*cos(30°)/2/π = √3/2*R*w(t)*cos(30°) = 3/4*R*w(t)
Like there is no external motor the rotational velocity of the disk is a function of time: w(t)=w0-d/(d+v(t)*t)
So the screw-thread is turning at ws(t)=√3/2*w(t) on the disk

When I attach at time ‘t0’ the spring the angular velocities are changed and I need to take in accound the inertia of the screw-thread. At time = t1, I stop to count the energies.

With the spring the angular velocity of the disk is changed:
wr(t)=w(t)-(√3/2+1/2)RF/Ir*(t-t0)

And the thread is also changed in:
wsr(t)=√3/2*wr(t)-1/2*RF/Iy*(t-t0)

For a small angle from the time t0 I attached the spring, (t1-t0) near equal to 0 so -(√3/2+1/2)RF/Ir*(t1-t0) near to 0 and -1/2*RF/Iy*(t1-t0) near to 0, the energies are counted from t0 to t1, the energies are:

The energy won by the spring is :

+(wsr(t1)+wrs(t0))/2*2*RF=√3/2*(wr(t1)+wr(t0))/2*2*RF

The energy lost from the torque of the force F on the disk, at distance R from the center of the disk is :

-(wr(t1)+wr(t0))/2*√3/2*RF

The energy lost from the force F on the axis ‘y’ on the disk is:

-(wr(t1)+wr(t0))/2*1/2*RF

The energy lost by the center of mass is:

 -3/4*RF*(wsr(t1)+wsr(t0))/2  = - 3/4*√3/2*RF*(wr(t1)+wr(t0))/2

The sum of energy is well at:

- 0.28*RF*(wr(t1)+wr(t0))/2

16 minutes ago, swansont said:

And for that you can't assume the spring has a constant force. 

Why ? for a small angle of study δ=1e-10rd, the distance increased by the spring is sqrt(3)*δ*R, it is 3.46e-11 m, the force is constant for that small difference of length. And it is possible in theory to have a "device" like a spring but with a constant force.

22 minutes ago, swansont said:

and you were doing an analysis for a complete turn

No, for a small angle of rotation δ. And it is possible to have a device composed of several springs to have a constant force:

 

 

1 hour ago, swansont said:

how do you account for the change in the moment of inertia without the mass of the bolt being known?

For example, with a bolt of 1000 kg with a radius for the bolt at 0.2 m, the moment of inertia could be at I=20 (it is an example), a spring with a force of 1N, with w=10rd/s and a study for δ=1e-10 rd. The time of study is dt=δ/w=1e-11 s. The torque is T=0.2 Nm. The angular acceleration will be  T/I=0.01 rd/s². The angular velocity at the end of 1e-11s will be 1e-13 rd/s compared with w = 10 rd/s, I supposed it is constant or don't change the result enough to have the sum at 0.

2 hours ago, swansont said:

That's the sort of detail you should include when presenting a problem such as this.

Of course, sorry for that miss.

 

2 hours ago, swansont said:

And I have explained why it's not. 

The angular velocity I supposed constant ?

 

2 hours ago, swansont said:

Some of the energy terms here have to be mass dependent, and I don't see any mass terms in your equations. The torque exerted by the spring will depend on the spring constant, and I don't see that referenced anywhere in your analysis.

I thought I could only do the sum of energy without the mass IF I compare with the same device but without the spring and for a small angle of study.

 

So, like I'm not able to study the transient sum of energy, I take a motor, I will count the energy I give to the motor to let constant 'w'. Before I attached the spring, I supposed all the parameters of the device like constant, I mean the bolt doesn't rotate around itself (no friction), the center of mass of the bolt rotates at 'w', the disk rotates at 'w' and the center of mass of the bolt is moving more and more far away from the center of the disk. The sum of energies of the closed device :{external power + motor + bolt + disk } is constant. The motor needs an energy but the center of mass will increase its kinetic energy.

 

At time=0, I add the spring:

The motor need to give an extra energy because there is the spring:

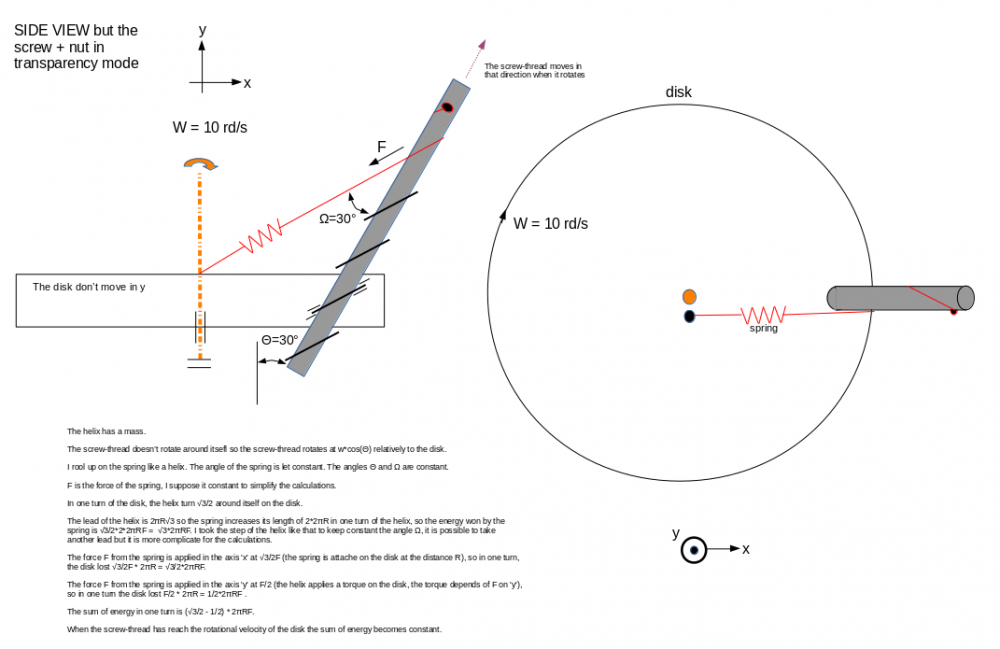
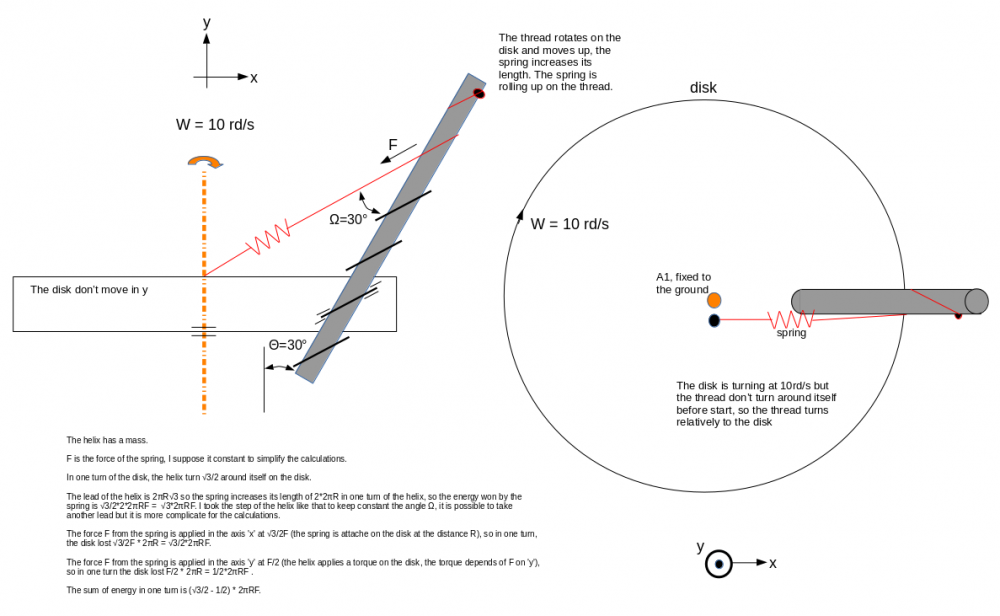
b) The force F from the spring is applied in the axis 'x' with an angle of 30° on the disk, then the force that works is √3/2F, so in δ, the disk lost -√3/2F * δR = - √3/2*δRF.

c) The force F from the spring is applied in the axis 'y' with an angle of 60° so the force that works is F/2 (the helix applies a torque on the disk, the torque depends of F on 'y'), so in δ the disk lost F/2 * δR = - 1/2*δRF

I win the potential energy from the length of the spring:

a) The lead of the helix is 2πR√3 so the spring increases its length of 2*2πR in one turn of the helix, so the energy won by the spring is √3/2*2*δRF = + √3*δRF. I took the step of the helix like that to keep constant the angle Ω

And I lost the energy that the spring recovers from the movement of the center of mass (farther from the center of the disk):

d)/ The center of mass of the helix changes its radius, the difference of length is δR*sqrt(3)/2  for a δ angle of the helix but the helix rotates at cos(30°) of the rotational velocity of the disk and the force is at 30° so the energy lost is - 3/4*sqrt(3)/2*δRF. I lost that energy because I can’t recover it with another device.

For a small angle of rotation, the bolt doesn't have time to rotate around itself because its angular velocity is 0 rd/s when I attach the spring. So the center of mass will move like no spring. I can take an angle of study of 1e-10 rd, with a mass of the bolt at 1000 kg and the force of the spring at 1 N.

 

 

 

9 hours ago, swansont said:

The bolt rising adds potential energy,

Do you mean potential energy from gravity ? There is no external gravity.

The sum of energy of the closed device: disk + bolt is conserved (there is no friction). The center of mass of the bolt moves more and more far away from the center but this will change the angular velocity of the disk. It is possible to add a motor to the disk and keep constant the rotational velocity of the disk. The energy from the motor goes to the kinetic energy of the bolt. Again, the sum of energy is conserved in the close device (even composed of a motor if I take in account the energy I give to the motor).

 

My work, suppose the energy is conserved without the spring. And for a small angle of rotation I have the energies due to the presence of the spring:

 

a) The lead of the helix is 2πR√3 so the spring increases its length of 2*2πR in one turn of the helix, so the energy won by the spring is √3/2*2*δRF = + √3*δRF. I took the step of the helix like that to keep constant the angle Ω

b)/ The force F from the spring is applied in the axis 'x' with an angle of 30° on the disk, then the force that works is √3/2F, so in δ, the disk lost -√3/2F * δR = - √3/2*δRF.

c) The force F from the spring is applied in the axis 'y' with an angle of 60° so the force that works is F/2 (the helix applies a torque on the disk, the torque depends of F on 'y'), so in δ the disk lost F/2 * δR = - 1/2*δRF .

d)/ The center of mass of the helix changes its radius, the difference of length is δR*sqrt(3)/2  for a δ angle of the helix but the helix rotates at cos(30°) of the rotational velocity of the disk and the force is at 30° so the energy lost is - 3/4*sqrt(3)/2*δRF. I lost that energy because I can’t recover it with another device.

The sum of energy for an angle δ is (√3/2 - 1/2 -3/4*√3/2) * δRF = - 0.28 * δRF

 

1 minute ago, swansont said:

It won't have time to rotate?

I mean around itself. For a small angle and because the bolt has a mass. The center of gravity of the bolt rotate like the disk but the bolt doesn't rotate around itself.

 

2 minutes ago, swansont said:

Why will it do this? Are you claiming there is no friction between the threads, and the bolt is otherwise unimpeded?  

The disk rotates around itself at w. The bolt rotates with the disk but the bolt doesn't rotate around itself at start. The bolt inside the disk is fixed to the disk, the disk rotates clockwise at w, so if you are on the disk you see the bolt rotates counterclockwise. No friction, correct.

 

6 minutes ago, swansont said:

You might be better served starting with a simpler system and see if you can solve that.

I added the consequences about the energy because I add the spring. Without the spring is conserved, I add the spring and I calculate the energies. I gave only the differences.

35 minutes ago, swansont said:

And you have a spring attached to it, which would tend to keep it fixed with respect to the disk.

The spring will give a clockwise torque to the bolt and it will start to rotate. I gave the calculation for an angle of 2pi but it is possible to study for a small angle, in that case the thread don't have time to rotate (around itself).

 

35 minutes ago, swansont said:

But why would it remain fixed?

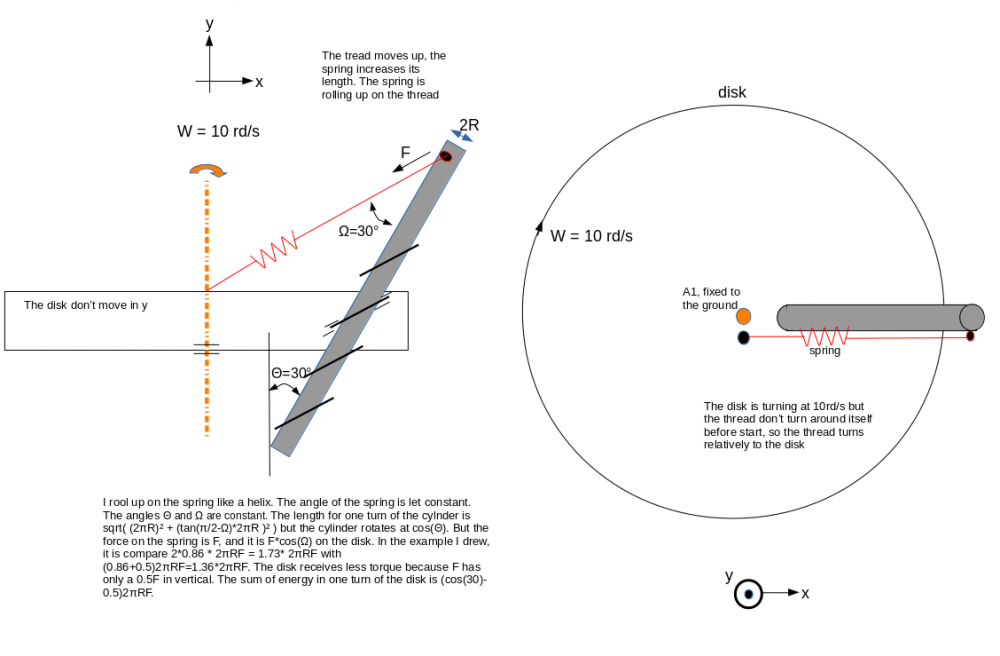
The bolt will rotate relatively to the disk and move. The center of gravity of the bolt will move more and more far away from the center of the disk. In my calculations I forgot the work lost because the center of gravity moves it is 2piRF  *  3/4*sqrt(3)/2, because in one turn of the disk, the bolt rotates only at w*cos(30°) and the angle of the force is at 30°. In one turn of the bolt the center of gravity moves of 2pi*R*sqrt(3)/2. Even, with that work, the sum is not at 0.

On 9/24/2018 at 6:20 AM, swansont said:

There is no relative motion of anything that would affect the bolt.

The disk rotates but the bolt doesn't rotate around itself so if you are on the disk you see the bolt rotates counterclockwise. Without friction nor the spring it is always like that.

 

 

23 minutes ago, swansont said:

why is the turning of the bolt coupled to the rotation of the disk?

Because there is a nut inside the disk. The disk rotates at 'w' when I start to count the energy. The bolt doesn't turn around itself when I set on the nut, the bolt is at -w*cos(30°) relatively to the disk when the spring is attached and the nut is set on.

 

28 minutes ago, swansont said:

You don't really show your work in enough detail.  

I give only the energies in comparison with the device without the spring (the energy is conserved with or without the spring). When I add the spring there is only the energy wins by the length of the spring and the energies lost by the torques from the force F on each axis 'x' and ''y'. What do you need ?

I redraw the start position without transparency and corrected the images:

 

 

 

 

 

8 hours ago, Strange said:

(an illegible image doesn’t count)

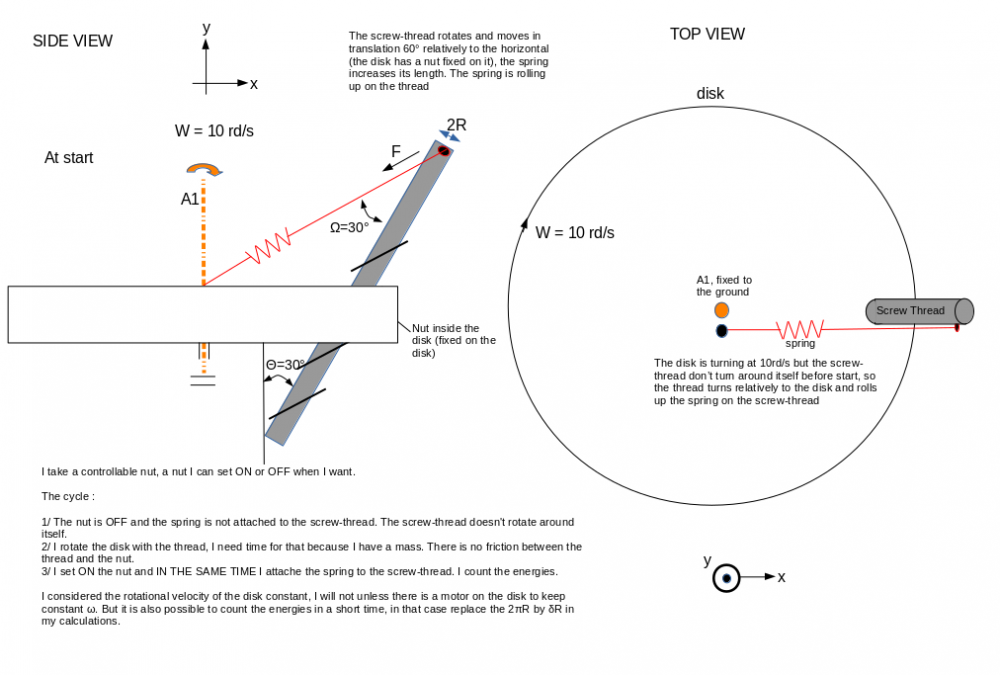
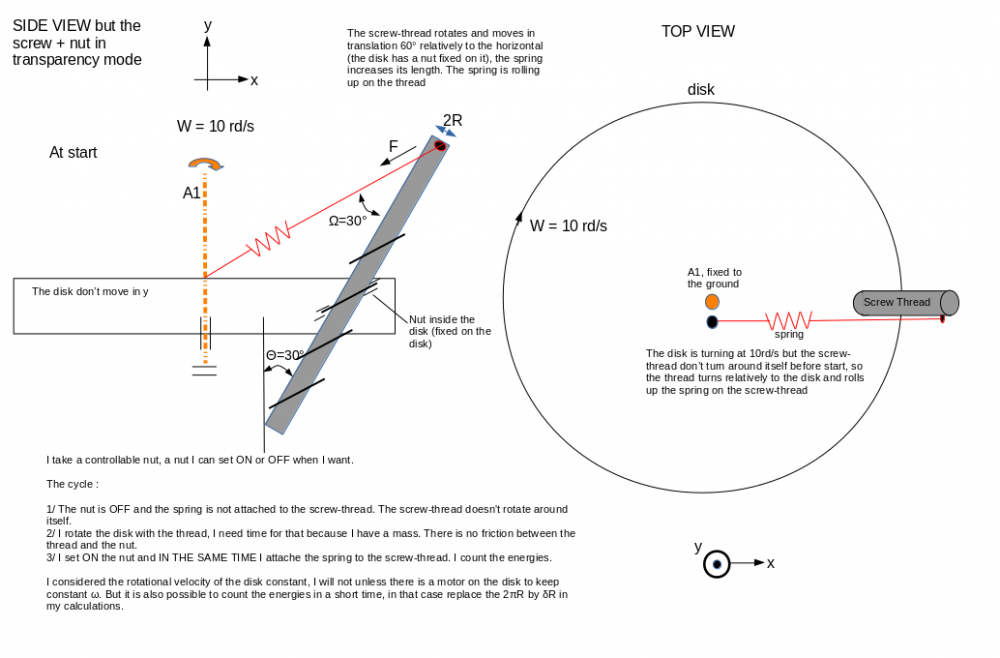
The device is a disk in rotation around the orange axis. The disk rotates only, don't move in vertical translation. There is a hole inside the disk (hole at 30° relatively to the orange axis). In that hole I fixed a controllable nut. Controllable nut because I want to control the time the nut works, I can set OFF/ON the nut, it is simply walls that moves. I passed through the nut a screw thread. That's all. I drew 2 views, the left view is a side view and the right a top view. In the left view, I drew the thread by transparency to see the thread. Before start, the screw thread doens't rotate around itself. The device-nut is OFF, the spring is not attached on the thread. After, I rotate the disk at w=10rd/s for example, I need time for that. I set ON the device-nut and I attached in the same time the spring to the thread, and I count the energies.

It it easier to take a controllable nut, because I know the rotational velocity of the disk (it is not an acceleration). The controllable nut is only retractable walls, it is just to simplify the calculations.

 

 

 

 

Nothing relative to my old post. I try to find my mistake. It is a classical simple mechanics device. Maybe the rotational velocity of the helix ?

I try to find my mistake about that device:

After a while the device is like that:

 

My logic : the device without the spring conserved the sum of energy, so I add the spring and I watch what I recover and what I need, the sum must be at 0  too. But here I find a difference, I don't find my mistake.

@Mordred: thanks for your help, yeah, I will study again my device with your advices, I think there is a problem too with the geometry when the device is deformed.

 

36 minutes ago, Strange said:

As you are either too lazy or too stupid to find your own mistakes, why should anyone here help you?

Waouhh, you can close all forums on earth. I hope the life will help you to understand what you are.

Note: the device is not isolated but the external device that controls the device counts all the energy in/out so the sum of the energies in/out must be at 0.

13 hours ago, Strange said:

What is the point? You have created an example that is so complicated that (1) you are not able to find your mistake and (2) you are unable to explain it to anyone else so they can find your mistake (if you were able to explain it, you would probably find the error).

I suspect the error is because you are making all sorts of physically impossible assumptions and so your example is meaningless. But I dont know and I don’t care (and I doubt anyone else does).

Energy IS conserved so your broken example is pointless.  

So, again, what is the point of this thread? Shall we just ask the mods to close it as a a waste of everyone’s time?

You asked me some questions, tell me details about springs, etc. I replied with that document. Have you read the 30 pages ? I explained all the device in detail. It is not because I took simplifications the device is false, in the contrary, it could be easier to find the mistake. The point of this thread is to break the law of conservation of the energy, with a counterexample, nothing else.

I translate a resume, maybe it could be clear like that.

det2.pdf

3 minutes ago, swansont said:

But you don't have gravity. Balls on a spring don't act like water under gravity.

Ok,I understood.

1 minute ago, Strange said:

But molecules of a fluid are not attached to springs.

Each is attracted by gravity. My springs are theoretical. I calculated several devices and each time I found the sum of the energy at 0.

 

3 minutes ago, Strange said:

It doesn't make much sense.

It is because you focused yourself on the technology not the theory.

1 minute ago, Strange said:

But it isn't water. It is a collection of (non-physical) spheres all pulled in one direction by (magical) springs. How can they exert pressure? What are they made of? How rigid or compressible are they? You would need to know these things to calculate the pressure they cause.

Even, it is a theoretical device, the sum of energy must be at 0. I can choose the perfect spheres in theory, to have the pressure. Molecules of a fluid does it so theoretical spheres can do the same.

1 minute ago, Strange said:

The springs only press (or pulls?) on the bottom of the container.

The springs pull.

 

1 minute ago, Strange said:

Not the sides.

Why not the sides ? The sides have pressure like the sides have pressure in a glass of water under gravity.

 

3 minutes ago, Strange said:

What is the source of this pressure? 

All the spheres are attracted in direction of the green line, so they pressure all they can, like molecules of water can do under gravity.

 

4 minutes ago, Strange said:

How do you calculate the pressure on the sides the container?

I have the force of the springs, so I have the pressure. I gave the force of the springs per volume like that I can change the diameter of the blue spheres.