SophiaRivera007

I have question regarding moles conversion. What are the mole conversion formulas involving grams & formula units?

First, let V_A represent the volume of liquid A, and let V_B represent the volume of liquid B, in 1 kg of mixture. Then, 850x(V_A+V_B) = 1 kg (of mixture). In addition, 1000V_A+600V_B = 1 kg (of mixture). We have here two equations with two unknowns (V_A and V_B). Solve for V_B. The mass of liquid B in 1 kg of mixture is 600V_B, which is equal to 264.7 grams.

Thank you AshBox. I find the perfect solution.

The density of two liquids (A and B) is given as 1000 kg/m³ and 600 kg/m³, respectively. The two liquids are mixed in a certain proportion and the density of the resulting liquid is 850 kg/m³. How much of liquid B (in grams) does 1 kg of the mixture contain? Assume the volume of the two liquids is additive when mixed.

Assuming you are not including air resistance (which would make this problem far, far harder) the kinematic equations would be the usual [math]s= (a/2)t^2+ vt+ d[/math] where a is the acceleration vector, v is the initial velocity vector, and d is the initial position vector. Separating x (horizontal) and y (vertical) components and taking the initial speed to be "v" and the intial position to be d= (0, 0), we have [math]x= v cos(30)t=(\sqrt{3}/2)v t [/math] and [math]y= (-g/2)t^3+ v sin(30)= -4.9t^2+ (0.5)vt[/math] where v is the initial speed.

 

Since the ball is to end up "20 meters away, the top edge is 5 meters above the throwing point", x= 20 and y= 5.

 

Solve the two equations [math](\sqrt{3}/2)v t = 20[/math] and [math]-4.9t^2+ (0.5)vt= 5[/math] for t and v.

Thanks For the solution. Is there any online solutions available to find Acceleration unit conversions or force unit conversion tools?

I am not from science student. I have to do some basic examples like this to help one of my friend.

Hello everyone,

Last day I had debate with my friend. She asked me this question:

Does entropy increase with time ? Or Does it make Time?

I have think on it but I couldn't answer it. Can anyone please help me to find this answer.

If a ball is thrown upward at an angle of 30 with the horizontal and lands on the top edge of a building that is 20 meters away, the top edge is 5 meters above the throwing point, what is the initial speed of the ball in meters/second?

Help me with initial steps.

Thank You AshBox, This will help me.

The modern loadline - the descendent of the plimsoll line is quite complex at first glance but easy if you look hard.

 

There are two sections - a roundel with a horizontal line through it with two letters (AB, LR, NV etc.). The letters tell you which Authority has classified the ship as safe and measured her safe load (American Bureau of Shipping, Lloyds Register, Det Norske Veritas etc.) The Horizontal line tells you where the sea will come up to when the ship is in a safely fully-loaded situation in salt water and in the summer. This is known as the Summer draft - this is the line from which the others are calculated.

 

Beside the roundel will be a branched symbol - this shows the level of the sea when the ship is in a safely fully-loaded condition in other sea conditions. All the other marks are calculated such that if a vessel is loaded to her summer draft and she goes into other situations (with a different density water) then the sea will come up to the other marks - and vice versa.

 

The Marks are as follows - on the left of the tree at the very top is TF for tropical fresh; this water is warm and has no salt in it. Below that is F Fresh water; no salt but not warm. On the right of the tree at the top is T for Tropical, and going downwards S Summer, W Winter, and the lowest line WNA Winter North Atlantic. Tropical fresh water is the least dense - it is warm and has no salt in it. Winter North Atlantic is the most - it is very cold and salty.

 

If the vessel is fully loaded in Arctic waters (ie the water is at the winter north atlantic marks WNA) when she gets to the warmer waters she will be slightly lower in the water (such that the water now reaches her Summer marks, if she then made a river passage into say Manaus she would be much lower in the water such that she was now riding with her Tropical Fresh Marks at the waterline.

 

The summer loadline is calculated by the shipyard which built the ship, the designers who laid the plans, the owners, and most importantly a group called the Classification Society. The Classification Society (the "Class") is an internationally recognized organisation who vet plans for ship, check the build process, survey the new ships for quality, and regularly inspect and survey ships during their trading life. The other loadlines are calculated using simple physics and agreed standards for the density and temperature of water in various parts of the world.

 

You ask about the stability of the ship - this has very little to do with the loadline; the stability depends on the overall design and most importantly the cargo plan - ie where the mass is. Basically, you have two centres of flotation; the centre of gravity and the centre of buoyancy - ideally you want the centre of gravity to be a little below the centre of buoyancy. This area is the purview of the Master Mariner (again with recommendations and rules from the Class) - a badly loaded ship will easily sink or break apart at the first sign of bad weather or adverse sea conditions

Thank you so much for guide me.

Can anyone help me to solve this?

A lifeguard who can swim at 1.2 m/s in still water wants to reach a dock positioned perpendicularly directly across a 550 m wide river.

a) If the current in the river is 0.80 m/s, how long will it take the lifeguard to reach the dock?

b) If instead she had decided to swim in such a way that will allow her to cross the river in a minimum amount of time, where would she land relative to the dock?

IMG_20161230_171327.jpg

 

If the above configurations are correct, it looks to me that the triangle can be either type 1, 2, 3.

I don't know how you can rule out triangle 2.

 

So IMO the answer is 5.

Thanks for easy solution Mr. michel123456

I have read about plimsoll lines, while loading a ship, care is taken it should not be overloaded. Its load depends on density of the see in which it floats. the ship will shink if its load exceeds.

Now my question is how to indicate depth up to which a ship can shink? And at what density value? which ensures stabilty and safety of

the ship.

Hello all,

I was practicing some problems and I come across this question :

Is triangle ABC with sides a, b and c acute angled?

1. Triangle with sides a², b², c² has an area of 140 sq cms.
2. Median AD to side BC is equal to altitude AE to side BC.

Which one is the right answer? And How?

1. Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
2. Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
3. BOTH statements (1) and (2) TOGETHER are sufficient but NEITHER statement ALONE is sufficient to answer the question asked.
4. EACH statement ALONE is sufficient to answer the question asked.
5. Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked; additional data specific to the problem is needed.

Golden ratio - Wikipedia

https://en.wikipedia.org/wiki/Golden_ratio

In mathematics, two quantities are in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities. ... where the Greek letter phi ( φ {\displaystyle \varphi } or ϕ {\displaystyle \phi } ) represents the golden ratio. Its value is: φ = 1 + 5 2 = 1.6180339887 … .

Decimal‎: ‎1.6180339887498948482... A...

Hexadecimal‎: ‎1.9E3779B97F4A7C15F39

Binary‎: ‎1.1001111000110111011

 

Thank you for great information.

Definition: The golden ratio, also known as the divine proportion, golden mean, or golden section, is a number often encountered when taking the ratios of distances in simple geometric figures such as the pentagon, pentagram, decagon and dodecahedron. It is denoted, or sometimes.

 

Using The Golden Ratio to Calculate Fibonacci Numbers

 

The Golden Ratio to calculate Fibonacci Series:

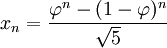
The answer will be equal to the addition of the previous two terms, as a whole number:

 

I.E.:

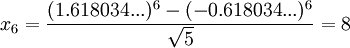
When I used an online calculator for this, I only enter the Golden Ratio to 6 decimal places & I got the answer 8.00000033. A more accurate calculation would be closer to 8.

Thank You AshBox. I have tried this equation and it gave me exact result which I was wondering about.

Hello, everyone

This is my first forum. I need help to find the nth term of Fibonacci series with the golden ratio. Can anyone help me to know about golden ratio and its equation? and how to find Fibonacci series from it.