Iggy

Perhaps.

 

Let me think about it...

 

If this is something that has never been explored then I think it would make an interesting problem to solve. For example, if fish under an amber or red light don't school together by color then we'd know it is a visual cue. Otherwise it may be a behavioral cue and fish may not actually know what color they are.

 

I wonder if it is a question that has been answered.

Ok. That all makes sense. But different races of people are built differently. Caucasians are built for power, throwing and lifting things. East Africans are great at distance running, and west africans/carribeans are built for speed. It's all in their bodies. For example, East Africans tend to be taller, with slender frames, and large lungs. But west Africans are shorter, and naturally have more muscle, and a chemical in their blood that helps with the large burst of power which comes in the form of sprinting? Are we more like dogs? Different breeds, yet we can breed together to make mixes

 

 

I have heard that genetic studies and other research has disproved the idea that physical and behavioral qualities are a function of breeding populations. Here are some applicable quotes:

• Keita, S O Y et al. 2004. "Conceptualizing human variation". Nature 36 (11s):

  "Modern human biological variation is not structured into phylogenetic subspecies ('races'), nor are the taxa of the standard anthropological 'racial' classifications breeding populations. The 'racial taxa' do not meet the phylogenetic criteria. 'Race' denotes socially constructed units as a function of the incorrect usage of the term."

• AAA 1998:

  "Evidence from the analysis of genetics (e.g., DNA) indicates that most physical variation, about 94%, lies within so-called racial groups. Conventional geographic 'racial' groupings differ from one another only in about 6% of their genes. This means that there is greater variation within 'racial' groups than between them."

• Lee et al. 2008:

  "We caution against making the naive leap to a genetic explanation for group differences in complex traits, especially for human behavioral traits such as IQ scores"

• Harrison, Guy (2010). Race and Reality. Amherst, Prometheus Books:

  "Race is a poor empirical description of the patterns of difference that we encounter within our species. The billions of humans alive today simply do not fit into neat and tidy biological boxes called races. Science has proven this conclusively. The concept of race (...) is not scientific and goes against what is known about our ever-changing and complex biological diversity."

• Roberts, Dorothy (2011). Fatal Invention. London, New York, The New Press:

  "The genetic differences that exist among populations are characterized by gradual changes across geographic regions, not sharp, categorical distinctions. Groups of people across the globe have varying frequencies of polymorphic genes, which are genes with any of several differing nucleotide sequences. There is no such thing as a set of genes that belongs exclusively to one group and not to another. The clinal, gradually changing nature of geographic genetic difference is complicated further by the migration and mixing that human groups have engaged in since prehistory. Human beings do not fit the zoological definition of race. A mountain of evidence assembled by historians, anthropologists, and biologists proves that race is not and cannot be a natural division of human beings."

Linking physical or behavioral standards to breeding groups or 'races' looks like something rather rejected by modern science.

A couple years ago 6 goldfish were born from the same batch of eggs and from the same female in my outdoor pond. 4 are black, 2 are orange, and one is yellow. They are all the same size. As they swim, the four black ones always stick together (usually touching or no more than a couple inches apart)—same for the 2 orange. The yellow one is usually by itself.

 

My question is, how does a goldfish know what color it is? I couldn't find a quick answer online.

though he claims that it agrees up to powers of [math]\frac{1}{c^2}[/math]).

I do.

 

It's quite approximate and weak-field-limit of me, but that's just the way I talk. Who can't talk in terms over c squared? Quite dielectric.

No, it doesn't, I think the term you are looking for is "dialectic", "dielectric" is something totally different and makes no sense in the context. Besides, I explained to you repeatedly that the two sentences are not connected logically so, why do you insist in beating up the strawman you have created?

So... you aren't just mistaking my meaning, you are literally mistaking my words?

 

How fun!

 

If we were involved in something dialectic then it would suggest that there were a difference of opinion, but I assure you that is not the case. It's just that you said two wildly different things, and that is *dielectric*. Perhaps you could look the word up, and consider your position, and get back to me, because either "Schwarzschild coordinates are the standard", or "the coordinate speed of light isn't physical". You'll have to pick one or the other, and I guarantee you the dictionary says that the two are dielectric.

 

As explained several times already, this is clearly incorrect. Using your notation:

It's good to terms of -c^2. If you're good to salt then you know exactly from whence it came, and I'm a little embarrassed you ask.

 

They are physically dielectric.

This sentence is meaningless.

 

Dielectric means that you can't get from one to the other.

 

My hope for you faded fast. We don't understand each other.

 

I'll welcome your solution to Shapiro delay as proffered in post 3, or I'll welcome your insistence that nothing non-local is physical. I'll welcome either thing you've said, but they are fiercely dielectric. You can't get from one to the other, you know?

 

The forces of the universe will keep those assertions apart despite your best efforts.

Sure it is, it points out that the variability is applied to a unphysical entity, to the coordinate speed of light

I apologize profusely.

 

Is the variable speed of light the unphysical entity, or the "standard answer", both of which you'd said.

 

Could you please just say one is right and one is wrong so I can understand what you mean?

 

You were right before and wrong now, or right now and wrong before? I can't tell until you say it explicitly. Is it that the "variability is applied to an unphysical entity" or is it that "Schwarzschild coordinates are standard"?

 

I'm happy with either. They are physically dielectric. Can't you choose one thing of which you've said?

Sure it is, it points out that the variability is applied to a unphysical entity, to the coordinate speed of light

I'm sorry... the "coordinate speed of light" is unphysical, or "Schoolchild coordinates are the standard". Which were you saying? It looks above like you just negated something you said earlier. Were you ok with that as long as you're interjecting with me now?

 

It's a bit difficult to tell. Can you just quickly say "the coordinate speed of light is unphysical, and therefore the earlier thing I said about it being the standard answer is just my best attempt at a pail stain on the carpet".

 

Can't you just say that? Or some humerus variation of it? It would end our confrontation immediately.

 

Tell me about it. The speed of light is variable in Schwarzschild coordinates.

Correction: the coordinate speed of light is variable in Schwarzschild coordinates.

 

That isn't a correction. That is something logically equivalent to what I said. I'm sure Euclid made some point about things logically equivalent to a mutual party are logically equivalent to themselves.

 

The speed of light in a certain set of coordinates doesn't need corrected as the certain coordinate speed of light in coordinates.

 

That is just you skipping the issue as always, I hope. I hope for you as always.

 

This unphysical effect is not used in the derivation of the Shapiro delay.

Please derive Shapiro delay in a way that reflects nothing of Schwarzschild coordinates. While you're at it, please say that post 3 has nothing to do with anything real or physical. Thank you.

The answer in terms of Schwarzschild coordinates is the standard, mainstream answer.

The use of the Schwarzschild metric in figuring out the delay does not validate in any form the fringe concept of "variable light speed".

Tell me about it. The speed of light is variable in Schwarzschild coordinates.

 

How wrong can one person be?

 

Which of the two above quotes would you like to retract? I'll be happy with either, but you still haven't answered.

The point was that you used the MINKOWSKI metric in your attempt to show that the distance between rockets is constant.

Yes, I'm perfectly capable of doing that.

 

When do you plan to retract your false statement that the Shapiro delay somehow proves the "slowing" of light speed?

If,

 

The answer in terms of Schwarzschild coordinates is the standard, mainstream answer.

then the radial coordinate velocity of light is,

 

[math]v_c = \pm \left(1- \frac{r_s}{r} \right)[/math]

 

and in terms of acceleration of gravity, g, and two radial points, A and B...

 

[math]v_{BA} = \left(1- \frac{gr}{2c^2} \right)[/math]

 

(where A is further than B and [math]v_{BA}[/math] is the average velocity of light between the two as measured by A)

 

If true then we get Shapiro delay for a round trip A->B->A...

 

[math]\Delta \tau = \Delta t_{flat} \left(1 + \frac{gr}{2c^2} \right)[/math]

 

and then light is slowed relative to flat spacetime, and many experiments have confirmed this, therefore,

 

Shapiro delay confirms it.

You have to decide if you're the sort of person that says "the answer in terms of Schwarzschild coordinates is the standard" or decide if you're the sort of person that denies that Shapiro delay originates in a variable speed of light.

 

Declaring both is incongruent.

 

Are you more interested in proving yourself (and post #3) correct, or proving me wrong?

You did not use the Rindler metric in computing the distance, aas you should have, you used the Minkowski metric.

Distance is constant in the Rindler metric a priori.

 

A rindler observer at x=1 is always at x=1, and the same with an observer at x=2. The distance between them is constant one by definition (it's assumed by the metric). Constant distance is proven in the derivation of the metric, not with the metric.

 

It's like asking someone to use a meter stick to prove that the meter stick is one meter. It's a confused question.

The simple answer is that you are trying to calculate the proper length using the Minkowski metric [math]ds^2=dx^2-(cdt)^2[/math], when , in reality, the metric is Rindler: [math]ds^2=(d \zeta)^2-(1+\frac{g \zeta}{c^2})^2 (c d \tau)^2[/math] where [math]\tau, \zeta[/math] are respecively, the proper time, proper distance measured by one of the accelerated observers. I have pointed out your mistake repeatedly in this thread, in different ways, this is yet another way to point out why your claims are wrong.

I appreciate your feedback, unfortunately we are no closer to a common understanding.

 

Both your metric and mine are Rindler, and they are physically equivalent. I will explain in a moment. I should first say that the t variable on the right hand side of your equation is not proper time, but rather coordinate time. This is common to all metrics (the t and r on the right hand side of the Schwarzschild metric, for example, are coordinate time and radial distance).

 

In fact, you rightly solve the metric above to get the following:

 

...null geodesics and to make [math]ds=0[/math] in the Rindler metric above. You would get... the correct formula of the coordinate speed of light for the accelerated observer is [math]\frac{d \zeta}{d \tau}=c(1+g \zeta/c^2)[/math]

If [math]d \zeta[/math] and [math]d \tau[/math] were proper distance and time then that wouldn't be a coordinate speed (which it should indeed be). It would be a proper speed.

 

More important to your point, however...

 

 

 

...is dependent on the acceleration and on the coordinate x. The elegant way of showing that is to remember that light follows null geodesics and to make [math]ds=0[/math] in the Rindler metric above. You would get [math]d \zeta=(1+g \zeta/c^2)(c d \tau)[/math]

That is, the correct formula of the coordinate speed of light for the accelerated observer is [math]\frac{d \zeta}{d \tau}=c(1+g \zeta/c^2)[/math].

 

According to your above logic, the observer at [math]x=0[/math] will measure the speed of light to be [math]v_x=0[/math], which is clearly absurd. The reason is that your formula, wherever you picked it up from (since you show no derivation) is incorrect. The correct formula is, as derived above , [math]\frac{d \zeta}{d \tau}=c(1+g \zeta/c^2)[/math]. This means that an observer at [math]\zeta=0[/math] measures the speed of light to be [math]c[/math] , as one would expect. As the observer accelerates away from the light source, the coordinate speed of light decreases, following the rule [math]\frac{d \zeta}{d \tau}=c(1-g | \zeta |/c^2)[/math]. At the Rindler horizon [math]\zeta=\frac{c^2}{g}[/math] so [math]c=0[/math]. A pulse of light emitted when the accelerated observer is already past the Rindler horizon, will never "catch up" with the accelerated observer.

The Rindler metric I gave is more common than yours (it is found on wiki you'll notice). Yours can be found on the last link I gave to JVNY (here).

 

Mine:

 

[math]ds^2 = (ax)^2(dt)^2 - dx^2[/math]

 

Yours:

 

[math]ds^2 = (1+ax_i)^2 dt^2 - {dx_i}^2[/math]

 

The difference between them is nothing more than a shifting of the x-axis origin by 1/a. In geometry it is called a coordinate translation. In other words, plug [math]x = x_i + 1/a[/math] into my line element and you will get yours. The x axis has been relabeled -- it has been shifted (which makes no physical difference).

 

The rindler horizon in my metric is at x = 0 and proper acceleration, a, starts at x = 1/a

The rindler horizon in your metric is at x_i = -(1/a) and proper acceleration, a, starts at x_i = 0

 

Of course, this means that the observer at x in my line element has a different speed of light from the observer at x_i in yours, because we are talking about two different observers with a distance 1/a between them.

 

 

As an analogy, if I said "Mt. Everest is 4,650 meters tall from its base", it makes no sense for you to object by saying "No, Mt. Everest is 8,848 meters tall from sea level". It is an obfuscation, not a disagreement.

 

 

My speed of light:

 

[math]v_c = ax[/math]

 

where my x is the same as your [math]x_i + 1/a[/math]... therefore my speed of light rewritten in your relabeled x-axis:

 

[math]v_c = a(x_i + \frac{1}{a})[/math]

 

[math]v_c = ax_i + 1[/math]

 

My speed of light is the same as your speed of light. You've just found a line element where the x axis is shifted by 1/a. Mt. Everest can be both one height from its base and another from sea level.

 

This absolutely does not change the conclusion I made -- that the coordinate speed of light is 100 times greater 100 times further from the horizon.

 

 

According to your above logic, the observer at [math]x=0[/math] will measure the speed of light to be [math]v_x=0[/math], which is clearly absurd.

No, that's either a typo or you're misunderstanding how to use the metric. The observer at x = 1/a will measure the speed of light to be zero at x = 0. The observer at x = 1/a does all of the measuring to determine the coordinate speed [math]v_c = xa[/math].

 

In my metric, the Rindler horizon is at x=0 which is why the coordinate speed of light is zero there (just like it would be zero at the Schwarzschild horizon).

 

In your metric the Rindler horizon is at x = -1/a (remember, the x axis has been shifted by 1/a between them), and the observer at x = 0 does all the measuring. That is why plugging -1/a into your speed of light equation gives zero. The observer at x=0 measures the coordinate speed of light to be zero at the horizon.

 

 

I understand that you are trying to show that coordinate speeds have no physical meaning, but if you understand what the coordinates mean I think there is a good amount of meaning. There is, after all, no way to discuss non-local speeds in GR except via coordinate speeds.

 

Denying physical meaning because GR works with any coordinate system is a bit like saying "this building could be measured in feet or meters and they give different values therefore the height of the building has no physical meaning".

---

 

 

 

I agree with this. What I did in the other exercises was to proportionately adjust all of the clocks' tick rates to the same rate (the farther rearward, the more elapsed ticks show on the clock than actual ticks of time for that rocket's clock). I think that you would call this putting all of the clocks on the same coordinate time. That eliminates the time dilation effect. It leaves only the distance effect. If you calculate the speed of light using the proper distance, then you get the speed of light slowing the closer the rocket is to the rear of the accelerating row (or the deeper in a gravitational well).

Ok, I think I gotcha.

Start with two ships, one at x=99.98 and the other at x=100. They accelerate simultaneously and flash a light at each other. Their acceleration rates are 1/99.98 and 1/100, respectively. Next, as you did before use the relativistic rocket formulas to determine the coordinate time that each light flash takes to cross the 0.02 proper distance and strike the other ship. You should find it to be 0.020002 (same in both directions). The coordinate speed of light is still less than c (0.02/0.020002), but it is getting very close to c. This is just an example, but I expect that those of you with better math skills than I have can prove that at any distance away from the origin the coordinate speed will remain below c (I think that it will asymptotically approach c, but I cannot be sure).

 

I forgot to answer this part, sorry.

 

It seems you're finding the coordinate speed of light where the t axis is made by the worldlines of the accelerating ships, and the x axis is made by the lines of simultaneity in the inertial frame. The problem I tried to touch on in a rush yesterday is that time dilation isn't accounted for in that case.

 

As an analogy, if someone sat near the event horizon of a black hole with rockets firing at enormous acceleration in order to hold their position then they would see the universe above them unfold at an extremely rapid rate. Light would move from one side of a galaxy to the other in an instant (from their perspective). If they set themselves up as the origin of a coordinate system then they'd need to account for time dilation to account for the increased coordinate speed of light above them.

 

The natural way to do this in the case of acceleration is rindler coordinates in which the speed of light is [math]v_x = x \cdot g / c[/math]. In your example, an observer at x=1 is considering the speed of light of someone at x=100. The speed of light in that case is,

 

[math]v_x = 100 \cdot 1 = 100[/math]

 

In other words, the speed of light is one hundred times less for someone one hundred times closer to the rindler horizon.

 

Let's do that in real-world numbers...

 

Let's say I am in a rocket accelerating at 100,000 km/s². To my right is a line of rockets with less and less proper acceleration, and to my left is a line with greater and greater such that we maintain proper distance. I calculate my distance to the Rindler horizon...

 

[math]x_0 = \frac{c^2}{g_0} = \frac{(299792 \ km/s)^2}{100000 \ km/s^2} = 898752.4 \ km[/math]

 

100 times this distance is 89,875,243 km, and the coordinate speed of light there would be...

 

[math]v_x = \frac{xg}{c} = \frac{89,875,243 \cdot 100,000}{299792} = 29,979,200 \ km/s[/math]

 

one hundred times the local speed of a ray of light.

Here is a recap and a reopening of the question of the coordinate speed of light in the accelerating frame as a function of the distance from the rear (which should be like the distance from a gravitational mass). I think that the result utilizes parts of the posts from each of md65536, Iggy and xyzt.

 

As md65536 suggests, consider a row of separate ships at rest in an inertial frame that are then simultaneously accelerated (rather than trying to accelerate a single object that has the same length as the row). Each ship accelerates at a proper rate inversely proportional to its distance from the origin. For example, the ship that starts at x=0.5 accelerates at a=1/0.5, or a=2. The ship that starts at a=1 accelerates at a=1/1, or a=1. As Iggy states, under these conditions the ships undergo "Born rigid" motion: they remain together in a shared accelerating reference frame; they keep their same proper distance in that accelerating frame; they agree on simultaneity; they always have the same velocity relative to the inertial frame; and their worldlines in the inertial frame are hyperbolas. Their clocks do not run at the same rate in their frame. The farther forward a ship is, the faster its clock runs. However, the rate is proportional to distance, so each ship behind the front can program its clock to automatically scale up its elapsed time proportionately and thus keep its clock synchronized with the front clock. Iggy advises that the front clock's time is the conventional measure of time in the accelerating frame; it is called the coordinate time of the frame. The time that we measure in that frame when we determine the speed of light in the frame is coordinate time, and so I think that the speed of light in that frame is its coordinate speed.

 

As the ships start to accelerate, the front ship flashes a light toward the rear. The Minkowski diagram for the inertial frame is as follows (ships' worldlines are hyperbolas; light flash's worldline is the arrow):

 

inertial.png

 

Because the ships are all in the same (accelerating) reference frame, we can Lorentz transform the light's path into the ships' frame. The light's worldline is no longer a straight 45 degree line. Rather, it is curved:

 

worldline.png

 

To make the effect clearer, we can diagram the marginal amount of coordinate time that it takes for the light to travel successive equal segments in the ships' frame (here done using distance increments of 0.02). It takes successively greater coordinate time to travel equal segments the farther toward the rear of the row (left in the diagram) that the light is traveling. In coordinate time, light is always traveling less than c, and increasingly less as it moves rearward:

 

marginal.png

 

Notice that the curve flattens out toward the front of the row (toward the right). This suggests that the coordinate speed of light over successive equal increments is higher toward the front (the right), but at a decreasing rate. It suggests that the coordinate speed will not exceed c. This agrees with xyzt, who states that the speed of light is not proportional to the distance from the origin, and more specifically that the speed of light will not exceed c at distances farther away from the rear. Xyzt prefers not to use calculations, but Iggy you can confirm that the coordinate speed of light does not exceed c as follows.

 

Start with two ships, one at x=99.98 and the other at x=100. They accelerate simultaneously and flash a light at each other. Their acceleration rates are 1/99.98 and 1/100, respectively. Next, as you did before use the relativistic rocket formulas to determine the coordinate time that each light flash takes to cross the 0.02 proper distance and strike the other ship. You should find it to be 0.020002 (same in both directions). The coordinate speed of light is still less than c (0.02/0.020002), but it is getting very close to c. This is just an example, but I expect that those of you with better math skills than I have can prove that at any distance away from the origin the coordinate speed will remain below c (I think that it will asymptotically approach c, but I cannot be sure).

I think the thing is that accelerated coordinates usually transform away from the horizontal Cartesian-like time coordinate. My understanding is that they should look more like...

 

 

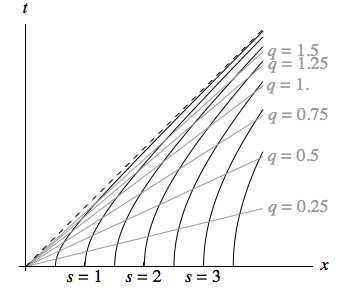
from this site. Or...

 

 

 

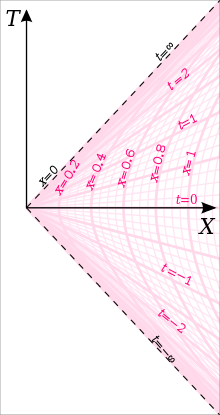
From wiki.

 

 

I think everything you're saying about the spatial coordinate is good, but the time coordinate would spread out as it fans right to reflect how clocks tick faster further from the origin. A light ray at 45 degrees around the middle of these diagrams would cross about one unit of t for every unit of x, but if you imagine traveling far from the origin where the temporal lines are really spread out, a light ray could cross a lot of hyperbolic spatial lines between each temporal coordinate line.

 

Hopefully I'm making sense.

 

I found, also, an interesting site comparing the speed of light in a uniformly accelerating frame, and a uniform gravitational field...

 

Speed of Light in a Gravitational Field

 

Actually, this site:

 

http://www.pitt.edu/~jdnorton/teaching/HPS_0410/chapters/general_relativity_pathway/uniform_acceleration.html

 

about the diagrams, for sure

Apologies for the delay in responding. I've been away from the site awhile. Hectic Holidays.

 

There is nothing special about "the v=0.6c frame".

Agreed.

 

Besides making the gamma factor an easy rational number, there's nothing significant about 0.6

 

 

Also what I said, is that you tried to demonstrate that the distance stayed constant in the launcher frame (and you failed).

 

[your bold]

But your attempt at proving that the "distance is constant" used length contraction, so you are contradicting yourself or you do not realize that you have actually (as you admitted at the end of your post) actually calculated the length in the lab frame. See your [math]L=L_0 \sqrt {1-v^2}[/math]

 

[your bold]

I didn't try (and fail) to calculate the v=.6 distance relative to the lab frame, nor did I actually calculate the v=.6 distance relative to the lab frame.

 

I very clearly showed (with JVNY's diagram), calculated (with equations), and explained (with words) that the *proper distance* remained constant, not the spatial distance in the lab frame.

 

Let me find the post...

 

 

 

 

Given JVNY's derivation (and illustration) of his thought experiment:

 

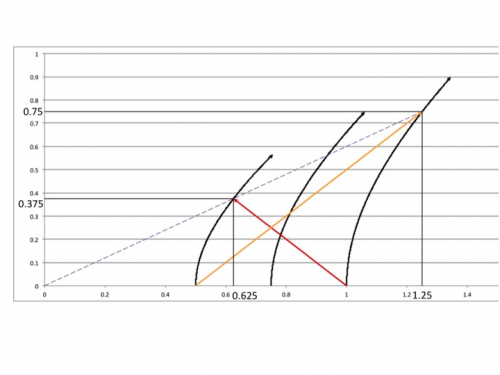
The proper distance at t=0 is given along the x axis as:

 

[math]\sigma = 1 - 0.5 = 0.5[/math]

 

The proper distance at the dotted line between the accelerated hyperbolic worldlines is given from the numbers in this frame by length contraction:

 

[math]\sigma = L_{0}\sqrt{1-v^{2}} = (1.25-0.625)(\sqrt{1-0.6^{2}}) = 0.5[/math]

 

 

 

So, I'm calculating the *proper distance* (an invariant quantity) between the fore and aft observers. The proper distance is what an at-rest observer measures between two simultaneous events.

 

The first equation calculates the proper distance by nothing more than taking the difference in x coordinates in the lab frame since the rest distance is the proper distance at t=0 in this frame. The answer is 0.5. One could more formally use the Minkowski interval to get the same answer:

 

[math]\sigma = \sqrt{\Delta x^2 - \Delta t^2} = \sqrt{0.5^2 - 0^2} = 0.5[/math]

 

 

The second equation finds the proper distance between v=0.6 events (along the dotted line). The events are simultaneous from the accelerating observers' perspective (i.e. in an inertial frame with v=0.6c rightward velocity relative to the launch frame).

 

It is done by length contraction,

 

[math]\sigma = L_{0}\sqrt{1-v^{2}} = (1.25-0.625)(\sqrt{1-0.6^{2}}) = 0.5[/math]

 

where [math]L_{0}[/math] is the spatial distance between events in the lab frame (where the events are not simultaneous), and [math]\sqrt{1-v^{2}}[/math] is the inverse of the v=0.6c gamma factor. Multiplying them gives [math]\sigma[/math] (the proper distance where the events are simultaneous). The answer is again [math]\sigma = 0.5[/math] meaning the *proper distance* is constant at the two times we sampled. And, considering the objection to length contraction above, we can again use the spacetime interval to verify:

 

[math]\sigma = \sqrt{\Delta x^2 - \Delta t^2} = \sqrt{0.625^2 - 0.375^2} = 0.5[/math]

 

 

Sorry to go on and on, but it's worth explaining in detail the actual purpose and successful results above. If you are still saying that the proper distance between uniformly accelerating observers can't be constant if the observers have different accelerations then it seems like you would have to explain why these observers with unequal accelerations have constant proper distance at two arbitrary times. That is to say, why does the lead observer measure the distance to the aft observer as 0.5 at both tau=0 and tau=0.6931?

 

The same calculation can be done, and the same question asked, at any velocity shy of c.

 

 

The motion is not Born rigid and this problem has nothing to do with Born rigidity, you are dealing with three particles that all have different speeds in any frame you consider, so, there is relative motion between them. As such, their relative distances, contrary to your claims, cannot be constant. Quite the opposite, it is variable.

 

In the launcher frame, the speeds are [math]v_i=\frac{a_i}{\sqrt{1+(a_it/c)^2}}[/math], i.e. they are all different (and they do not depend in any fashion of the initial positions [math]x_{0i}[/math]).

It looks like you're missing a variable in the numerator of that equation. The equation finds the velocities of the rockets relative to the launch frame, so it can only say when things have the same velocity in that one frame. The start of the thought experiment (t=0) should be the only time that is true.

 

In other words, that equation proves to us that...

 

 

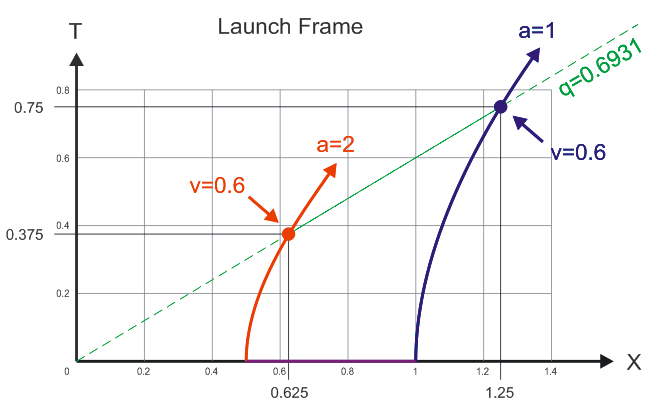
...the red dot and the blue dot are not horizontally aligned (neither is any other velocity we could mark on the hyperbolic worldlines except v=0 at t=0).

 

However, the green line is the line of simultaneity relative to the hyperbolic observers at those events, not a horizontal line. You wouldn't expect the events to be simultaneous in the lab frame -- you expect it in the 'momentarily comoving inertial frame'

 

 

As far as born rigidity... The uniform acceleration of Born rigid particles means the particles maintain their proper distance as they accelerate. You can imagine tying a string between the rockets/particles and having each accelerate such that the string doesn't strain. The OP imagines just such a system, and it is well-published that the following is true in such a system,

 

Trailing sections of the rod must undergo a greater acceleration in order to maintain Born rigidity with the leading end, and the required acceleration is inversely proportional to the distance from the pivot event

 

Born Rigidity, Acceleration, and Inertia

 

On the other hand, accelerating rockets that do maintain equivalent velocities in the lab frame would typically be called 'Bell's spaceships'. The rockets maintain equivalent accelerations and constant distance in the lab frame, but do not maintain a constant proper distance as they accelerate. In that case a string tied between them would stretch and break.

 

 

In the frame co-moving with any particle, the calculation is a little more complicated but the conclusion is the same, there is relative motion between the particles because, their speeds, as calculated from any such frames are variable and not equal. Indeed, the proper speed of the particle i=1 is [math]v_1=c * tanh (a_1 \tau/c)[/math].

That equation will tell you the velocity of the launch frame relative to the observer (it does it with tau rather than t is the only difference between it and the equation you just gave). By the principle of reciprocity, it gives numerically equal results. It is problematic for the same reasons I just was saying. It does not tell you the speed of one particle in a frame comoving with another.

 

 

The proper speed of particle i=2 is [math]v_2=c * tanh (a_2 \tau'/c)[/math]. [math]\tau'[/math] and [math]\tau[/math] are connected by the coordinate time [math]t[/math]:

 

[math]t=\frac{c}{a_1} sinh (a_1 \tau/c)[/math]

Again, the equation you have for 'coordinate time' is relative to the launch frame. I've said many times that the distance doesn't remain constant in any particular inertial frame. Because they're accelerating, the frame of measurement has to change as their velocity changes. The easiest way to do this is to set up an accelerating coordinate system (e.g. Rindler coordinates)

 

The solution in which we're interested is derived just above the paragraph and link I'll copy here:

 

This is the magnitude of the constant proper acceleration which the leading end of the rod must undergo in order to meet the stated conditions. Also, the reciprocal of this value represents the distance of the leading end of the rod from the pivot event. Trailing sections of the rod must undergo a greater acceleration in order to maintain Born rigidity with the leading end, and the required acceleration is inversely proportional to the distance from the pivot event

 

http://www.mathpages.com/home/kmath422/kmath422.htm

0.625/gamma

gamma = 1.25

Yeah, that's what I had

 

You may not realize that what you tried to prove is that [math]x_2(t)-x_1(t) = x_3(t)-x_2(t)[/math], i.e. the distance between the rockets stays constant in the frame of the launch pad.

No, it apparently stayed constant in the v=.6c frame, not the frame of the launch pad. JVNY calculated it earlier, and Md verifies the math. Also, Born rigidity has been around for about 100 years, I don't think you're about to disprove it. So...

 

there is no number since the proper distance between ships is a function of the proper time [math]\tau[/math].

No, not a function of tau. It is well-established science that the proper distance between accelerating observers stays constant if their acceleration is inversely proportional to their distance.

 

I, nevertheless, appreciate your insistence otherwise. It's like Christopher Hitchens said in Canada I think... He said "it might, in any case, give people to think about why do they know what they already think they know. How do I know that I know this, except that I've always been taught this and never heard anything else. It's always worth establishing first principles"

 

You've certainly challenged us to establish first principles, and I welcome the challenge and hope I haven't disappointed in the result.

 

Thank you, Md.

Md65536, do you wanna help us out?

 

A spatial distance of 0.625 in our frame is what in a frame of relative velocity v=.6c?

The answer in terms of Schwarzschild coordinates is the standard, mainstream answer.

Fair enough. Let's answer your Shapiro delay question in terms of Schwarzschild coordinates:

 

Q & A: How does Shapiro delay work

 

The rule about the speed of light being constant only applies locally to patches of spacetime small enough to be effectively flat, i.e. ones which can be described by special relativity. On a bigger scale, with gravity involved, phrases like "the same distance" become ambiguous.

 

Let's think of light from some distant star. There's an extra delay in how long it takes to reach us when the light happens to pass near the sun on its way. How come? We can describe it in a particular choice of coordinates, the Schwarzschild coordinates. Two things happen to the light as it goes near the sun:

 

1) Close to the sun, the effective rate at which time passes is slowed. According to local clocks there, the light is traveling at the usual speed, c, but we think those clocks are slow so from our point of view the light is going slower.

2. As it approaches and departs from the vicinity of the sun, the light travels extra distance, more than what you would calculate if you drew a big circle around the sun and took the diameter to be its circumference over 2pi. Space isn't Euclidean- the diameter of that circle is bigger than it should be based on the circumference. So the light has farther to go (as measured by local rulers) than it would if it weren't going near the sun.

 

These effects add up to give the Shapiro delay.

 

Should you say that under these circumstances the light travels farther? In our coordinate choice, that does account for half the effect.

 

Q & A: How does Shapiro delay work

You insisted earlier that Shapiro delay is due to light traveling farther than it would otherwise have to. In Schwarzschild coordinates that does account for half the effect. The other half is because "from our point of view the light is going slower".

 

Shapiro delay is an effect measured by our clocks here on earth, and it does indeed verify that light is slowed relative to our clocks here, and I am indeed happy that you accept Schwarzschild coordinates for proving this.

 

 

I ask the following question because you rejected my answer very aggressively: If a spatial distance is 0.625 in our frame, then what is the distance is a frame with a relative velocity of v=0.6c?

That is false, you are trying to act as a "teacher" but you keep piling up mistakes. For example, the most serious link you cite , the C.M.Will one, you took the citation not out of the Shapiro delay explanation paragraph but out of the following paragraph, his refutation of the Kopeikin paper (the one that claims to be measuring the speed of gravity). This nullifies your appeal to authority and invalidates your explanation. On the other hand, I provided the mathematical derivation of the Shapiro effect, there is nothing in it about the speed of light "slowing down". I also pointed out that the rays of light do not come anywhere close to the event horizon, contrary to your claim, you chose to sweep this error under the rug. The rays of light in discussion pass by at distances that are many orders of magnitude larger than the EH.

I will consider carefully what you say.

 

I explained this as well to you several times, last time in this post, that there is no number since the proper distance between ships is a function of the proper time [math]\tau[/math]. As such, it obviously varies with [math]\tau[/math]. What you are calculating is not the proper distance between the ships. You are calculating something else, I'll let you think about it.

The ships constitute a Born-rigid system, so the proper distance between them is not a function of [math]\tau[/math]. But, that isn't what I'm asking.

 

I'm saying that the following is an inertial frame:

 

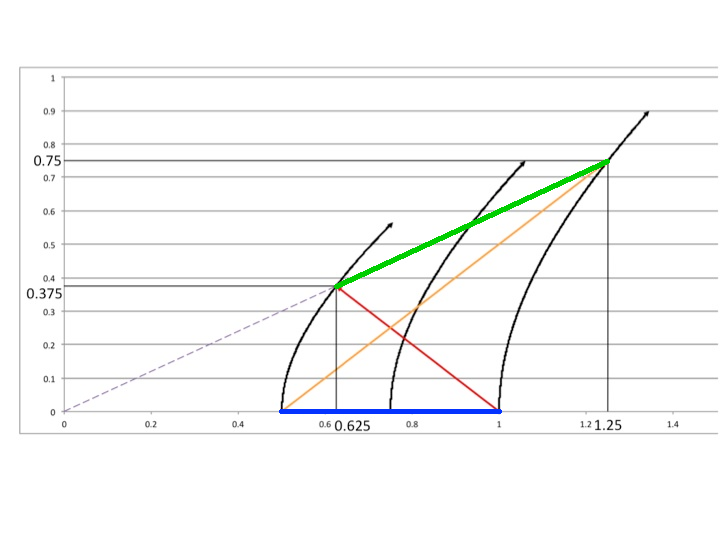
in which the spatial distance of the blue line is 0.5, and the spatial distance of the green line is 0.625. What is the distance of the green line in a v=0.6 inertial frame?

 

You say there is no number, but I assure you the question I just asked has a numerical answer.

 

 

 

 

 

---

 

 

 

 

 

First note, primarily to Iggy:

 

Aside from any reasoning mistakes you may or may not have made, you appear to be using fairly specific (but not widely used) definitions of a number of terms that become somewhat ambiguous in general relativity. If these terms are used at all, they will often be context dependent and should be defined for the purposes of a discussion if they are to be used at all. Velocity (outside of local velocity) is one such.

I've spoken of speeds in particular coordinate systems. For example, the first thing I said about the speed of light, and the first thing that found objection, and the thing that has been frequently quoted, is the following:

 

your diagrams in your pdf are Rindler coordinates. The speed of light in that case is [math]xg[/math] (where x is the x position and g is acceleration). As c and x are proportional in c = xg, the greater the x (i.e. the greater the distance from the mass) the greater the speed of light.

 

Is the speed in Rindler coordinates a coordinate speed? I dare say it is. But, I have not been ambiguous about what I was talking. From the start -- I didn't just say that it was a coordinate speed, I gave the specific coordinates to which I was referring, so I don't know why you are directing that comment at me.

 

 

You are also using terms like simultaneous and proper distance to refer to events relating to events that do not share an obvious inertial reference frame as if we are all on the same page (doing so is going to require further qualification).

If it isn't clear then I expect the following site would make it clear:

 

In other words, the accelerated clock's rate is identical to the clock rate in a "momentarily comoving inertial frame" (MCIF), which we can imagine is holding an inertial clock that for a brief moment slows to a stop alongside the accelerated clock, so that their relative velocity is momentarily zero.

 

Clock acceleration and timing

Any time I have spoken of simultaneity of an accelerating clock I have done so in the context of a 'momentarily comoving inertial frame'. I didn't think this was a problem because every participant in this thread spoke of light rays hitting distant accelerated objects simultaneously relative to accelerated observers before I joined the thread. I agreed with that conclusion, and spoke in the same terms.

 

Not to mention, you might note I wrote the following yesterday:

 

No doubt, any non-local speed in GR is ambiguous, but an ambiguous thing does not a constant and invariant thing make.

 

 

Thirdly, you appear to be privileging results derived from a specific coordinate system. The words/definitions/results derived are frequently only going to be useful within said coordinate system.

Indeed. If you open the PDF in the OP then you will see it is a diagram of a specific coordinate system. Subsequent questions asked by the OP dealt with that same coordinate system. It shouldn't be a surprise that I've been talking about that exactly.

 

 

 

These are all things that aren't really appropriate in a response to someone asking a question when they are learning SR/GR.

Let me ask you if post #3 is appropriate. It answers the OP entirely in terms of Schwarzschild coordinates which are irrelevant to the OP and the language of the OP -- like something copied out of the wrong book.

 

I'm glad you're here, and I welcome your participation in this thread immensely, but I think you've misjudged the previous discussion.

I asked you some questions, so please answer them. , I pointed out quite a few errors in your posts, may I suggest that you answer the points and stop trying to talk down to me?

 

I'm not trying to talk down. I gave my reasoning and cited three sources to answer your Shapiro delay question in post 73.

 

Before before you "pointed out quite a few errors" in that post I asked a very straightforward question.

 

Given that the blue line is 0.5...

 

What is the distance of the green line in a v=0.6c frame?

 

You have told me repeatedly that my use of the length contraction formula won't work, so I'm very curious what solution you find. Can you give me a number. This is literally the simplest question you could get in special relativity, and I'm just looking for a number.

 

Could you please give me a number so we can be on the same page?

Despite of your repeated claims, there is no "variable speed of light" and Shapiro delay doesn't "verify" any such thing, the Shapiro delay mainstream explanation (you can try MTW, Rindler, Moller, to name just afew), shows that the delay is due to the deviation of the geodesic from a straight line. I gave the mainstream explanation in this post, the one that you chose to ignore.

 

The blue line is 0.5 in the rest frame

Since you disagree with my calculation of the proper distance between the first and the third worldlines, could you please calculate the distance of the green line in a v=0.6 frame?

 

Thank you.

 

I should also mention -- I appreciate your persistence and dedication in neg-reppring all of my posts. Occasionally, I think you might forget one, but you are very meticulous and I can appreciate that quality.

 

Any case... the length of the green line?

You are playing word games

A site that says Einstein meant "velocity" rather than "speed" when he said "geschwindigkeit" is, itself, playing word games. I just corrected the site. Whenever Einstein says "velocity" in his early publications, one should never assume that he must be referring to a direction-dependent quantity.

 

Plus I gave two other quotes saying the same thing that use the english word "speed".

 

I'm sorry this appears to you as a word game.

 

so what would velocity/speed "slowdown" mean in your post on the explanation of the Shapiro delay be?

 

Contrary to your claims, there is no "speed slowdown" in the mainstream explanation of the Shapiro delay.

I didn't explain Shapiro delay -- I said that it verifies a variable speed of light. It is shown to do that because the speed of light approaches zero as light approaches an event horizon (either the horizon of a black hole or the horizon of rindler coordinates)

 

My claim also means that there are many sources saying the same:

The rule about the speed of light being constant only applies locally to patches of spacetime small enough to be effectively flat, i.e. ones which can be described by special relativity... Close to the sun... from our point of view the light is going slower.

 

University of Illinois - Department of Physics

On September 8, 2002, Jupiter passed almost in front of a quasar, and Kopeikin and Fomalont made precise measurements of the Shapiro delay with picosecond timing accuracy...

 

...several authors pointed out that this 1.5PN effect does not depend on the speed of propagation of gravity, but rather only depends on the speed of light [14, 288Jump To The Next Citation Point, 232, 49, 233]

 

- The Confrontation between General Relativity and Experiment - 3.43 - Clifford M. Will

since speed of light is reduced in the gravitational field, [math]c` < c[/math], travel time is increased... this is called the Shapiro delay

 

Gravitational Lensing - p.44 - Matthias Bartelmann (University of Heidelberg, Germany)

These are the citations, logic, and science I'm willing to devote to the subject. I would rather focus on the other thing we're talking about since it came up first and it's closer to the topic, so please forgive me if you keep talking about Sapiro delay and I keep failing to respond to it.

 

But your attempt at proving that the "distance is constant" used length contraction, so you are contradicting yourself or you do not realize that you have actually (as you admitted at the end of your post) actually calculated the length in the lab frame.See your [math]L=L_0 \sqrt {1-v^2}[/math]?

Distances can be constant in a length-contracted frame. I feel like I'm befuddling you.

 

 

As an aside, how did you get [math]v=0.6c[/math] in the above? The rockets have different proper accelerations, they have different speeds, so how did you get the value you plugged in?

It can be done with two equations of which I can think (both given on this page). I'll do a=1 and a=2 (the velocity should be 0.6 with both equations for both accelerations) like you ask me to demonstrate...

 

a=1:

 

[math]v = c \cdot \tanh{ \left( \frac{a \tau}{c} \right)} = \tanh{(0.6931)} = 0.6[/math]

 

[math]v = \frac{at}{\sqrt{1+ \left( \frac{at}{c} \right)^2}} = \frac{2 \cdot 0.75}{\sqrt{1 + (2 \cdot 0.75)^2}} = 0.6[/math]

 

a = 2:

 

[math]v = c\cdot\tanh{ \left( \frac{a \tau}{c} \right)} = \tanh{(2 \cdot 0.34665)} = 0.6[/math]

 

[math]v = \frac{at}{\sqrt{1+ \left( \frac{at}{c} \right)^2}} = \frac{2 \cdot 0.375}{\sqrt{1 + (2 \cdot 0.375)^2}} = 0.6[/math]

So... that's how it can be done... how one can get v = 0.6

 

JVNY also did the calculation earlier, but I don't remember what method he used

 

Yes, it was a typo, I corrected it. Doesn't change the fact that your "proof" failed. Try proving that [math]\frac{c^2}{a_3} (cosh(\frac{a_3T}{c}) - 1)-\frac{c^2}{a_2}(cosh(\frac{a_2T}{c}) - 1)=constant[/math], please.

Why would the proper distance traveled from launch pad to finish of the lead ship minus the proper distance of the middle ship be constant? Why would I attempt to prove that?

 

Nobody claimed those things were constant and it isn't logical or relevant to ask for that proof. The claim is that the distance between ships is constant, not that the distance traveled by any one ship is constant with the distance traveled by another.

 

 

That was really off base... let me draw a diagram and see if we can get on the same page...

 

Given the blue line is 0.5 in the lab frame, can you find the length of the green line in a frame with a relative leftward velocity of 0.6c (relative to the lab frame)?

 

I'm asking because it is necessary to answer the above question in order to calculate what we're doing -- the proper distance between them -- and it is quite literally the easiest problem relativity has to offer. If you're familiar with the Minkowski metric then it can be done in your head. A simple number for the length of the green line in the v=0.6 frame would delight me beyond telling.

 

Please don't answer that you've said previously that you don't type numbers, and I know your history shows a pattern such that you are inclined to point out an error in the last three paragraphs rather than answering, but I'm asking, please: you disagree with my number so... what is the length of the green line in a frame v=0.6c relative to the frame showed?

 

I asked IVNY to explain how he arrived to his conclusions, I asked you to justify your claims that velocity and speed are interchangeable.

Velocity and speed are equivalent in German because the same word in German means both.

 

The site JVNY quoted said "Since Einstein talks of velocity (a vector quantity: speed with direction) rather than speed alone...", but like I said, that site doesn't realize that the quote was originally written in German in 1916, and translated to English in 1920. Einstein's quote says "the law of the constancy of the velocity of light in vacuo... cannot claim any unlimited validity", and the word "velocity" there is a translator's choice. It could have just as easily and correctly been translated as "speed" (just like it was in the other two quotes I gave).

 

You are trying to answer the question posed to IVNY but your approach using length contraction is incorrect. Let's try again: the trajectories of the three rockets are [math]x_i(\tau)=x_{i0}+\frac{c}{a_i^2}(ch \frac{a_i \tau}{c}-1)[/math] with [math]i=1,3[/math] and [math]x_{i0}=0.5, 0.75,1.0[/math]. It is obvious that for any given [math]\tau >0[/math] [math]x_2(\tau)-x_1(\tau) \ne x_3(\tau)-x_2(\tau)[/math],

There are a couple of problems here. I'll address them at the end of the post as they require some latex

 

so a naive solution based on length contraction fails miserably.

Length contraction is what you get when one frame solves the distance of a length in another frame. It is an application of the Lorentz transformations (the transformation from one frame to another).

 

You may not realize that what you tried to prove is that [math]x_2(t)-x_1(t) = x_3(t)-x_2(t)[/math], i.e. the distance between the rockets stays constant in the frame of the launch pad.

Certainly not. Notice what I said in my last post:

 

So, the rest frame (the inertial frame, or lab frame) calculates that the proper distance between the front and rear rockets remains equal (always 0.5 in their frame)... these numbers work out in Rindler coordinates (in which all observers are taken to be at rest in their accelerated frame.

I'm calculating "their frame" (the accelerated observers). I'm not calculating distance in the lab frame.

 

Their proper distance is measured in their frame and that is what I calculated (which is to say... not the person on the ground doing the calculating, but them whom are accelerating doing the measuring)

 

JVNY said the same earlier:

 

In their frame, there is always 0.25 distance between rear and center, and 0.25 distance between center and front. In the inertial frame the distances length contract, however

In their frame the distance remains constant. In the lab frame it shortens.

 

 

Returning to the thing before... it looks like you mistyped/miscopied the equation for proper distance of uniform accelerated motion. The equation as given here (second one down) is:

 

[math](\frac{c^2}{a}) [\cosh(\frac{aT}{c}) - 1][/math]

 

and you wrote:

 

[math]\frac{c}{a_i^2}(\cosh \frac{a_i \tau}{c}-1)[/math]

 

so it looks like you squared the denominator of the first term rather than the numerator. However, even if you had gotten that portion correct, this still wouldn't work:

 

[math]x_i(\tau)=x_{i0}+\frac{c}{a_i^2}(ch \frac{a_i \tau}{c}-1)[/math]

 

Because [math]x_{i0}[/math] gives part of the distance in the lab frame and [math]\frac{c^2}{a_i}(\cosh \frac{a_i \tau}{c}-1)[/math] gives the other part in the accelerated frame. All distances must be measured in the accelerated frame in order to calculate the distance in the accelerated frame. One can't simply add lab frame proper distances to accelerated frame proper distances when the claim to which you disagree is that distance remains constant for observers undergoing these particular accelerations in their (accelerated) frames

 

On the proper distance, by setting the proper accelerations at 2, 1.33, and 1, one ensures that the ships always stay 0.25 apart in their own reference frame. This is explained more fully in http://www.mathpages.com/home/kmath422/kmath422.htm .

I don't see anything supporting your claim, why don't you explain, with math, in your own words , your claim. Please do so.

 

 

I do not see any valid calculations.

The part for which you asked -- the part about maintaining a constant proper distance -- can be quickly proved.

 

Given JVNY's derivation (and illustration) of his thought experiment:

 

The proper distance at t=0 is given along the x axis as:

 

[math]\sigma = 1 - 0.5 = 0.5[/math]

 

The proper distance at the dotted line between the accelerated hyperbolic worldlines is given from the numbers in this frame by length contraction:

 

[math]\sigma = L_{0}\sqrt{1-v^{2}} = (1.25-0.625)(\sqrt{1-0.6^{2}}) = 0.5[/math]

 

So, the rest frame (the inertial frame, or lab frame) calculates that the proper distance between the front and rear rockets remains equal (always 0.5 in their frame) while the front accelerates at a=1 and the aft at a=2. This is further verified by the definitional meaning of Rindler coordinates in which I've already run these numbers. All x coordinates maintain constant proper distance in Rindler (accelerated) coordinates, and these numbers work out in Rindler coordinates (in which all observers are taken to be at rest in their accelerated frame.

 

It is further cited in the link JVNY gave (2.9 Accelerated Travels)

 

And, here is another well-written article on Born rigidity reporting the same:

 

Likewise every other hyperbolic path asymptotic to the same light lines (i.e., sharing the same pivot event) maintains a constant proper distance from that event and, therefore, from every other path in this class. Hence, in order for our set of particles distributed along the x axis to accelerate while maintaining constant proper distances from each other, the magnitude of the constant proper acceleration of each particle must be inversely proportional to it's (signed) distance from the pivot event x_p. In other words, if x_j is the location of the jth particle at time t = 0, then this particle's constant proper acceleration must be a_j = 1/(x_j - x_p)

 

Born Rigidity, Acceleration, and Inertia

[edit]... I apologize. JVNY already gave this link in addition to the one directly above it. It continually amazes me how quick he finds these relevant links, reads them, and correctly reports and understands what they say. I'm struggling to keep up.

[/edit]

 

You are asking how acceleration of 2, 1.33, and 0.5 can maintain constant proper distance at a = 2, x = 0.5; a = 1.33, x = 0.75; and a = 1, x = 1. The bolded portion above answers that they do because they are inversely proportional. In other words, all three of those sets of numbers follows x = 1/a.

 

Cited by two good sources and solved by at least two independent methods, I don't understand how you can continue to object with nothing more than "explain, with math, in your own words".