timo

Random comments on your seemingly random questions: 1) Particle physics is indeed looking at debris to a very large extend. However, people are not looking for new objects in the debris. They look at the content and distribution of the debris and compare it with the predictions of the different mathematical models. 2) The reference to "statements about their encounters" does not refer to particle collisions (caveat: I am interpreting a single sentence out of context here - but modern particle physics did not exist during Einstein's lifetime, anyways). It refers to a key concept in relativity that comparing situations at different locations is tricky. It is not required that the objects in questions are elementary particles that collide. The famous spacefaring twins meeting each other after their space travel (or lack thereof) are would be typical situations that the statement refers to.

I did an interview for a newspaper article a couple of years ago. Me and a PR colleague talked with a journalist for about an hour in the morning. The journalist already had a vague idea about the topic and we essentially had a chat about it. The journalist then sent me the draft article in the evening. I sent him correction proposals that were all accepted. Nothing spectacular on this level. Still, there were a few takeaways from this experience: 1) It is the journalist's story. When you get the interview request you feel very important and in the center of things. But in reality you are just helping the journalist to write the article. This also why I said that I sent "correction proposals". The journalist is not required to send you the story beforehand or get your permission for publication. 2) I originally sent elaborated explanations to my corrections, explaining in which context the statement would be correct and when it would me misleading. I ran my corrections through our head of PR. He said a memorable sentence in the sense of: "that guy is a poor devil, a freelancer being paid per article written. Just send him corrections that he can accept or decline and don't cause him extra work". Point is: As a scientist you may be excited about the topic, and of course you expect the journalist to be exited, too. In reality, to the journalist your topic could as well be an orphan kitten that has been adopted by a dog: It is a story that gets the next article. 3) We had prepared lots of great diagrams but the journalist insisted on a photo of me, instead. My face is completely irrelevant for the science and even inappropriate for the fact that our results were achieved by a team. It is a manifestation of the journalist rule "no news without a face". Since I experienced this from the producing side, I often find myself re-discovering this: When a minister proposes something (that his employees worked out), when the director of a research institute is asked an expert opinion about a topic (which he bases on the work of the people actually doing the science - his employees) or -a current example of discussion in my family an hour ago- when the main discussion of the climate conference is how Greta Thunberg looked at Donald Trump.

There are two approaches here, the formal one and the brain-compatible one. 1) Formally: Realize that there are hidden coordinate dependencies. You are probably looking to construct a function p(y). Since y is the coordinate at the lower side, you have p(y) at the lower edge and p(y+dy) at the upper. This is (possibly) slightly different from p(y) (because of the displacement dy). If you call the difference dp, then p(y+dy) = p(y) + dp(y) = p + dp (note that dp can and will be negative). 2) Brain compatible: Put the equation first and then define the variables: The forces on top and bottom should cancel out. There force up is the pressure force p*A from below. The force from up is the pressure force p2*A from above the small fluid element plus the weight dw of the small fluid element. Since we are talking about infinitesimal coordinates, and since p(y) should be a function, it makes sense to say that p2 = p+dp, which you can then integrate over.

In my opinion, the content you listed is below the minimum required for AI (not really sure what "Data Science" is, except for a popular buzzword that sounds like Google or Facebook). More precisely: Apply these topics to multi-dimensional functions and you should have the basis of what is needed for understanding learning rules in AI. However: All of the content you listed is the minimum to finish school in Germany (higher-level school that allows applying to a university, that is), even if you are planning to become an art teacher. And Germany is not exactly well known for its students' great math skills. The course looks like a university level repetition of topics you should already know how to use, i.e. a formally correct way of things that were taught hands-on before. I do not think a more rigorous repetition of topics will help you much, since you are more likely to work on the applied trial&error side. Bottom line: If you are already familiar with all the topics listed, I think you can skip the course. If not, your education system may be too unfamiliar to me to give you any sensible advise. Btw.: University programs tend to be designed by professionals. So if a course it not listed as a mandatory, it is probably no mandatory.

By this standard, physics is not very strange most of the time.

The equation is not particular to Compton scattering. It is the relation between momentum and energy for any free particle (including, in this case, electrons). I am not sure what you consider a derivation or what you skill level is. But maybe this Wikipedia article, or at least the article name, is a good starting point for you: https://en.wikipedia.org/wiki/Energy–momentum_relation

There is no law of conservation of mass. Quite the contrary: The discovery that mass can be converted to energy, and that very little mass produces a lot of energy, has been a remarkable finding of physics in the early 20th century. The most well-known use is nuclear power plants, where part of the mass of decaying Uranium is converted to heat (and then to electricity). The more modern, but from your perspective even more alien view is that mass literally is a form of energy (I tend to think of it as "frozen energy"). In that view, you can take the famous E=mc^2 literally. There is a law of conservation of energy, but energy can be converted between different forms. In your example, it is converted from kinetic energy of the photons to mass-energy of the electron and the positron (and a bit of kinetic energy for both of them). Note that the more general form of E=mc^2 is E^2 = (mc^2)^2 + (pc)^2 with p the momentum of the object - it simplifies to the more famous expression for zero momentum. I say this to make the connection to your other question where you asked about this equation.

This post is a bit beyond the original question, which has been answered - as Psi being a common Greek letter to label a wave function and wave functions being used to describe (all) quantum mechanical states. I do, however, have the feeling that I do not agree with some of what your replies seem to implicate about superposition, namely that it is a special property of a state. So I felt the urge to add my view on superposition. Fundamentally, superposition is not a property of a quantum mechanical state. It is a property of how we look at the state - at best. Consider a system in which the space S of possible states is spanned by the basis vectors |1> and |2>. We tend to say that [math] | \psi _1 > = (|1> + |2>)/ \sqrt{2} [/math] is in a superposition state and [math] | \psi _2 > = |1>[/math] is not. However, [math] |A> = (|1> + |2>) / \sqrt{2} [/math] and [math] |B> = (|1> - |2>) / \sqrt{2} [/math] is just as valid as a basis vectors for S as |1> and |2> are. In this base, [math] | \psi _2 > = (|A> + |B>)/ \sqrt{2} [/math] is the superposition state and [math] | \psi _1 > = |A>[/math] is not. There may be good reasons to prefer one base over the other, depending on the situation. But even in these cases I do not think that superposition should be looked at a property of the state, but at best as stemming from the way I have chosen to look at the state. Personally, I think I would not even use the term superposition in the context of particular states (a although a search on my older posts may prove that wrong :P). I tend to think of it more as the superposition principle, i.e. the concept that linear combinations of solutions to differential equations are also solutions. This is kind of trivial, and well known from e.g. the electric field. The weird parts in quantum mechanics are 1) the need for the linear combination to be normalized (at least I never could make sense of this) and 2) that states that seem to be co-linear by intuition are perpendicular in QM. For example, a state with a momentum of 2 Ns is not two times the state of 1 Ns but an entirely different basis vector. Superposition in this understanding almost loses any particularity to QM. Edit: Wrote 'mixed' instead of 'superposition' twice, which is an entirely different concept. Hope I got rid of the typos now.

To turn rotational energy into electric energy you can indeed use dynamos, as you already assumed. Or better: Dynamo-like devices. The general term seems to be https://en.wikipedia.org/wiki/Electric_generator. Essentially, i.e. from a physics perspective, electric generators move around magnets in the vicinity of looped electric wires ("electro-magnets"). This induces a current in the wires. Doing this moving around in a controlled way generates a controlled current. Sidenote: I thought the general concept of a dynamo is a "turbine". But according to Wikipedia that refers to the moving part, only. Still, turbines are so closely related to electric power generation that looking up that concept may be relevant, too.

Thermodynamics, in its general meaning, is always equilibrium Thermodynamics. Calculations of processes assume that the systems go through a series of equilibrium states during the process, which is called a quasi-static process. Reversibility is not required for studiot's entropy change equation in the first post. The equation is fully applicable to bringing two otherwise isolated systems with different temperatures into thermal contact, which I will use as an example: In the theory of thermodynamic processes, both systems' states change to the final state through a series of individual equilibrium states (*). Because of their different temperatures and conservation of energy (and because/if the higher-temperature system is the one losing heat to the colder) the sum of entropies increases. In the final state, both systems can be considered as two sub-volumes of a common system that is in thermal equilibrium. Since the common system is in equilibrium (and isolated), it has a defined entropy. Since entropy is extensive, it can be calculated as the sum of the two entropies of the original systems' end states. As far as I understand it, removing barriers between two parts of a container is essentially the same as bringing two systems in thermal contact. Except that the two systems can exchange particles instead of heat. The two systems that are brought into contact are not isolated - they are brought into contact. If one insists on calling the two systems a single, unified system right after contact, then this unified system is not in an equilibrium state (**). And I believe this is exactly where your disagreement lies: Does this unified, non-equilibrated state have an entropy? I do not know. I am tempted to go with studiot and say that entropy in the strict sense is a state variable of thermal equilibrium states - just from a gut feeling. On the other hand, in these "bring two sub-volumes together"-examples the sum of the two original entropies under a thermodynamic process seem like a good generalization of the state variable and converges to the correct state value at the end of the process. (*): I really want to point out that this is merely a process in the theory framework of equilibrium Thermodynamics. It is most certainly not what happens in reality, where a temperature gradient along the contact zone is expected. (**): In the absence of a theory for non-equilibrium states this kind of means that it is not a defined thermodynamic state at all. But since there obviously is a physical state, I will ignore this for this post.

I assume you refer to my magnet example: The force between two magnets depends not only on their location, but also on their orientation. Take two rod magnets NS in one dimension which are one space (here I literally mean the space character) apart. In the case NS NS their attract. If one is oriented the other way round, e.g. NS SN, they repel each other. On other words: Their force does not only depend on their location, but also on their orientation (the equations in 3D are readily found via Google, but the common choice of coordinates may not obviously relate to what you describe). So for calculating forces or energies of magnets, you need their orientation as an additional parameter. This orientation can be expressed as a unit vector (and to relate to my first post: since this is a geometric and not an integration topic, unit vectors are better suited than angles).

It is hard to tell without knowing your "subject" or the variable. For spherical coordinates of a single location, the unit direction vector indeed supplies no additional information to the location vector. Maybe the direction refers to something else than the location? Like the state of a small magnet, which (ignoring momenta) is defined by its location and its orientation at this location. Or much simpler: Direction refers to the direction of travel. Another idea I could think of is that if your position and direction are data in a data set processed on a computer. Then, they could just be in there for convenience of the user or some (possibly overambitious) performance optimization of calculations that only need the direction and want to skip the normalization step. Just semi-random ideas.

Using unit vectors to define directions indeed contains the same information as using appropriate angles. And either can be used in conjunction with a radial coordinate to define location (but only the version with the angles is called spherical coordinates). Either version can be more appropriate for a practical problem, I think. In my experience, direction vectors tend to be more useful for trigonometric/geometric questions, and spherical coordinates tend to be more useful for integrals.

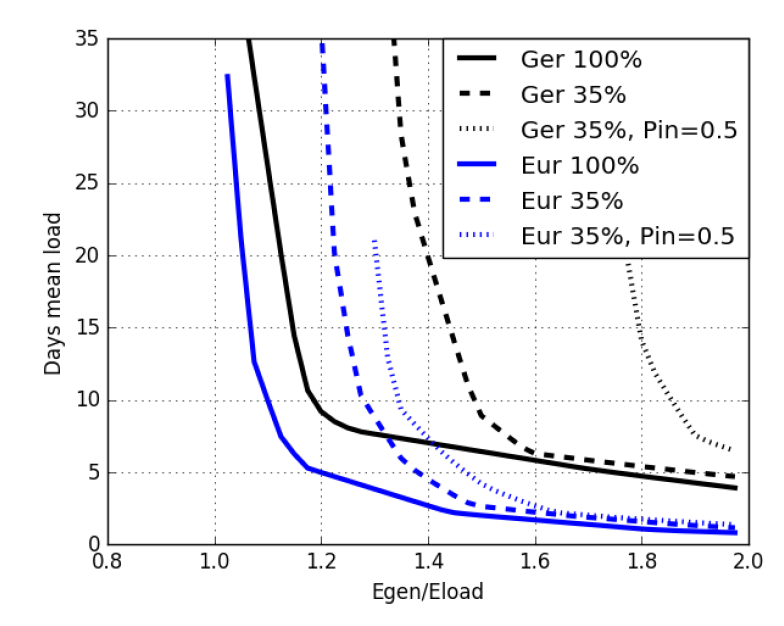
All of what you said is at least arguably true (including the part about technological alternatives, that I did not cite). I took the battery example from the introductory slides of a lecture on renewable energies, where it was meant as an approximation and a starting point for the students to possibly try objections on. One of the key factors for the calculation is, of course, the capacity required. For simplicity (and readily availability of a suitable plot from the same lecture ), let's restrict this to fully-renewable systems: The required capacity relative to the load is indeed influenced by the size of the area - it goes down with area, just as you stated. Perhaps not down to 1 day. While the "night with no wind" is a picture that everyone understand easily, it is too simple to understand why we need storage. "Several days with not enough wind in the region" is much better but less intuitive. And I have seen cases in which evidence suggested that in an economically-optimized calculation the storage demand is influenced by the annual fluctuations in renewable generations. It also strongly depends on the amount of renewable generation: If you accept that storage demand is driven by prolonged times of insufficient renewable generation, rather than complete absence, then it is clear that this demand gets smaller if you install more generation than the total electric energy demand suggests.Simply said (and ignoring power limits and efficiency losses for now): You have a trade-off between extra generation costs and extra storage costs. The image above is based on 8-year historic weather and load data with some fixed assumptions about the share of wind and PV generation (usually 1:2 or 1:3 in terms of energy) and a fixed spatial distribution of the PV panels and wind parks. Black curves correspond to isolated German systems, the blue curves are the corresponding extremes of loss-less capacity-unbound electricity transmission in Europe (defined as roughly the EU). The horizontal axis is the potential for electricity generation relative to the demand, the vertical one the required capacity for useable energy in units of days of mean power demand. The solid curves correspond to a storage that is perfectly efficient and not limited by input power. Detailed calculations of optimal scenarios, which also consider topics like adaptive demand that I did not cover in these posts for the purpose of keeping complexity down, end up with a generation ratio of around 1.1 to 1.3. So 7 days for the Ger scenario and 4 days for the Eur scenario may look realistic. The dashed curves correspond to 65% efficiency loss on power intake (35% return efficiency), which is realistic for chemical storage. The most prominent effect is that the location of the diverging capacity requirements shifts from 1.0 to some larger value. Lastly, the dotted lines show the capacity requirements with the additional constraint that the maximum charging power is 50% of the mean load power. As I hopefully made clear by now, the amount of required capacity depends on a lot of factors (some discussed and some more). More complex calculations tend to find a mix of long-term storage (cheap capacity, bad efficiency) and short-term storage (expensive capacity, good efficiency), but the mix depends on a lot of details, e.g. the assumed technology costs, which directly play into the the trade-off between extra installation and extra storage. The 30 days I used were the result of one of these calculations; I might indeed want to do the Europe-equivalent alongside to see the results there. I strongly doubt the 1-day capacity requirement for reasons hopefully made a bit more clear in my statements above. But even if the calculations came up with 16 G€/a, which is about 16% of the total cost of electricity including grid fees and taxes, there is one thing that I want to comment on that may or may not be clear to everyone: That number is on top of the other costs, not the new costs. With the ridiculously high number I estimated the difference is irrelevant (13 times as expensive vs. 14 times as expensive) but for smaller numbers this should be considered. I agree that there are a multitude of storage solutions. My current favorite (just for the coolness) is underwater pump storage, which may in fact be the technical realization of the compressed air bags you linked to. For me, who usually considers the energy system from an abstracted point of view, all of the alternatives to synthetic chemical fuels fall into the "limited by capacity costs" class of short-term storage and become just another technical realization of a battery. Redox-Flow batteries are the best candidate for not being capacity limited that I currently see (but have not investigated). For a company in the market, that wants to optimize revenue on the percentage-margin, the choice of technology of course may be very relevant. But they usually have a very different approach for decision making in the first place.

Not 100% certain what you mean. "Can't be contradicted" is not the same as "proven", especially in math. Any unproven theorem in math, say an unproven Millenium Prize Problem, is proof of this (silly pun intended). Because if they could be contradicted (more specifically: we knew a contradiction to the statements) then they were proven wrong. Accepting an argument as true is a much stronger statement than not contradicting it. Taking the liberty to modify your statement to "a proof is an argument that everyone [sane and knowledgeable implied] has to agree on" that is not too far away from what I said. The main question is where "everyone" lies in the range from "everyone in the room" to some infinity-limit of everyone who has commented and may ever comment on the statement. This limit would indeed be a new quality that distinguishes proofs from facts (to use the terms swansont suggested in this thread's first reply. I could understand if people chose this limit as a definition for a proof. But it looks very impractical to me, since I doubt you can ever know if you have a proof in this case (... but at least you could establish as a fact that something is a proof ... I really need to go to bed ... ). Fun fact: For my actual use of mathematical proofs at work, "everyone" indeed means "everyone in the room" in almost all instances. For me, the agreement of that audience would not be enough to call something a fact . (Okay... off to bed, really ....). It is, indeed. Maybe with an extra grain of elitism for not needing observations but relying on the thoughts of peers alone.

If you accept discovery of a particle as proof for a particle, then that is pretty much the usage of the terms in particle physics, where "evidence" is a certain amount of statistical significance and "discovery" is a certain larger amount of statistical significance (example link for explanation: https://blogs.scientificamerican.com/observations/five-sigmawhats-that/). That usage of the terms is, however, very field-specific. Other fields may have problems to quantifying statistical evidence. When I was a young math student, I thought about the same. Then in a seminar a professor asked me "what is a proof" and I told him something about a series of logical arguments that start from a given set of axioms. His reply was roughly "err .. yes, that too, ... maybe. But mostly it is an argument that other people accept as true". I think his understanding of "proof" may be the better one (keeping in mind that "other people" referred to mathematicians in this case, who tend to be very rigorous/conservative about accepting things as true).

Absolutely. Adding up thin shells to create the full sphere is actually a very common technique to access the volume, i.e. [math] V(r) = \int_0^r A(r) \, dr[/math] Well, picking up on the integration example: The average distance <r> of a particle from the center in a sphere of radius R is [math] <r> = \frac{1}{V(R)} \int_0^R \, r \cdot A(r) dr = \frac{1}{V(R)} \int_0^R \, r \cdot 4\pi r^2 dr = \frac{1}{\frac 43 \pi R^3} \left[ \pi r^4 \right]_0^R = \frac 34 R[/math] (modulo typos: Tex does not seem to work in preview mode ... EDIT: And apparently not in final mode. The result in the calculation above is <r> = 3/4 R). There is a general tendency that the higher the dimension, the more likely a random point in a sphere lies close to the surface. There is a famous statement in statistical physics that in a sphere with 10^23 dimension, effectively all points lie close to the surface. In all sensible definitions of volume and area I am aware of (at least in all finite-dimensional ones), volume has one more dimension of length than area. Hence, their quotient indeed has dimensions of length. I don't think the quotient itself has a direct meaning. But there are theorems like that a sphere is the shape that maximizes the V/A ratio for a fixed amount of V or A. I already commented on the dimensionality. But I still encourage you to just play around with other shapes: Cubes are the next simple thing, I believe.

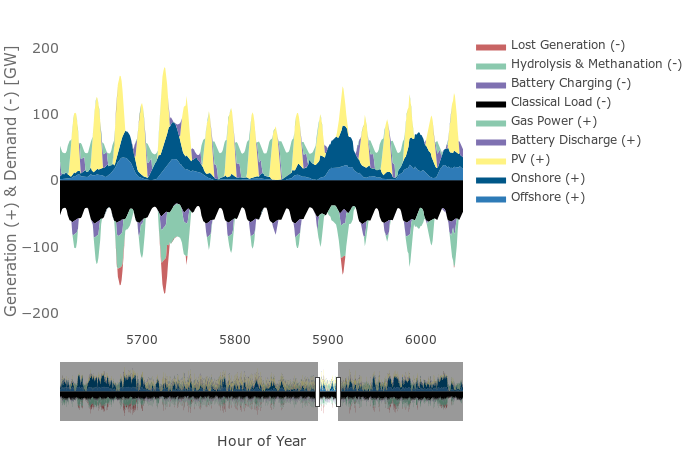
As stated before, battery storage is already used in the energy system. Just not to systematically balance renewable power generation. The most common application is balancing the discrepancy between electric power forecasts used for the operation planning and actual power generation and load. I believe that the Tesla battery mentioned by pzkpwf falls in this category. On a smaller scale, batteries are often used within private/business premises to maximize the use of self-generated photovoltaic power or as backup power source in case of failures (link). The topic of storing renewable energies usually comes up in the context of electricity generation from wind power and solar photovoltaic power (PV). Often in contexts like "the weather dependency of wind and PV make it impossible to create a reliable electric power supply" or "we need to solve the storage problem before we can build renewable power systems". The short answer why batteries are not considered as the storage solution is that they are too expensive for really large amounts of renewable wind and PV generation: Battery capacity costs money Fully-renewable power systems need large storage capacities - in the order of a month of electric power supply It is more economical to create synthetic fuels to satisfy this backup storage demand For a more detailed explanation, keep on reading ... Detail Explanation I'll use Germany as an example, because I have data for it at hand. At least the European weather conditions (and almost certainly also the northern American weather conditions) are sufficiently similar, anyways. Also, I will focus on wind and PV generation as well as batteries and synthetic fuel generation as possible storage options. There are many other options for generation and storage, and some can be very relevant for specific areas (pump storage in Norway, hydro power generation in Iceland, concentrated solar power in northern Africa, ...), but wind, PV, battery and hydrolysis are somewhat universally-relevant options. Wind and PV power generation depend on the weather and vary significantly over time, whereas the power demand (=load) is relatively stable. This creates an imbalance between generation and load that must be match by additional demand (or exports), curtailing of the power generation or additional generation (or imports). The following image shows an example of an optimized renewable energy system with onshore wind, offshore wind and PV as power generation, gas power as additional generation option, hydrolysis and methanation (the creation of hydrogen and subsequently methane from water and carbon) as additional flexible demand, no import/export, and curtailing where needed (called "Lost Generation", here). As you can see, batteries do play a role in the balancing: They are systematically charged by the daily PV peaks and discharged in the evening. The reason they do not cover all of the balancing demands is ultimately a question of economic viability and the cost of battery capacity. The high-frequency daily charging/discharging makes very good use of the battery capacity since the annual energy throughput is roughly 365 times the installed capacity - up until you have so much capacity that you don't fill it up every day and get diminishing returns. There are, however, lower-frequency storage demands, i.e. longer times of effective surplus or deficit power. An example are the 3-5 days of low wind power generation around hour 5800 in the plot above. Even the annual generation of wind power changes by ~10% between years and may have to be stored for bad years. The events occur relatively rarely, but are associated with lots of energy. For a fully-renewable power generation, the total capacity required of the storage system is significant. For the example system used in the plot above, 45 TWh of electric energy (-equivalent) storage are needed. Assuming 300 €/kWh battery costs and 10 years battery lifetime that means 1350 * 10^9 €/a costs for the storage alone. But the total cost of the German electricity system today is only 100 * 10^9 €/a. For low-frequency, high-capacity storage needs, the creation of synthetic fuels via hydrolysis (for Hydrogen) and possibly further steps (for Methane or theoretically even fluid fuels) is more suitable. It is associated with high losses, but fuels are very efficient to store in large quantities of energy over long time. So instead of using batteries alone, a mix of storage options is used. Highly efficient but capacity-limited battery storage for high-frequency storage and low-efficiency high-capacity synthetic fuel storage for the low-frequency storage. In the example of the plot above, the battery capacity is 120 GWh (i.e. 0.3% of the total capacity demand), but has an annual throughput of 30 TWh, whereas the fuel storage is 45 TWh with an annual electric energy output of 55 TWh (for reference, the total annual demand is 450 TWh).

The facility you are referring to is called the SSC, not SSSC. Or at least I have never heard anyone referring to it as SSSC. The site is not exactly in the vicinity of Stanford University, but about 2500 km away in Texas. Wikipedia has an article about it on https://en.wikipedia.org/wiki/Superconducting_Super_Collider, which answers your first question: About three times the size and energy of the LHC. Considering the Standard Model of Particle Physics, having had the SSC should have lead to the detection of the Higgs Boson sooner. The next proposed step after the LHC is a lepton collider, which allows more precise measurement on the physics discovered at the hardon collider (both SSC and LHC are hardon colliders). The lstest proposal of a lepton collider is the https://en.wikipedia.org/wiki/International_Linear_Collider (ILC). Given the time such projects take my guess is that having had the SSC ten years sooner than the LHC would simply have put us ten years closer to the ILC-like experiment (I don't expect that we have ILC results within the next ten years). Theoretically, the SSC could have found new physics/particles that the LHC cannot detect. But no one can know that. As the name suggests, the ILC indeed is an international project - as has been the LHC. I would not expect that these days anyone would plan a national collider experiment of that scope, anymore. While I was not around in science at the time SSC was planned, I imagine that the cold war was a reason why it was even considered as a national project. In fact, the Wikipedia article lists the end of the cold war as one of the reasons for the cancellation of the project.

Multiplying values with physical constants (like h-bar or c) can be considered as re-expressing the same value in a different measurement system (i.e. in different physical units). That is also true if the value is a physical constant itself (like G). In this case, the coupling constant of gravity has been expressed in a suitable form for a case where energies are measured in GeV/c². This is a very typical unit for energy in accelerator particle physics, where ~100 GeV/c² is a typical energy of a particle. Possible uses could be statements like "see how weak gravity is compared to electromagnetism, which has a coupling of 10^-2" (electric charges have unit 1, actual value is 1/137). The Planck mass/energy mp is the energy that elementary particles would need to have (in a simple quantum gravity) for their gravitational force to become comparably strong to the other forces. Hence, G*mp*mp = 1, which is approximately 10^-2. It should not be understood as a particle class of "Planck particles" or a source of energy. Notable objects which exceed the Planck mass are the earth and the moon. Their gravitational interaction with each other happens to be much larger than their electromagnetic interaction. That would remain true if their masses were expressed in units of GeV/c².

In a sense, getting to massless SM particles could be achieved by increasing the temperature in some region. But it would be more like an activation of the frozen Higgs field than a blocking. It is easier to explain coming from the high-energy side (high temperature), since that is the standard explanation for the Higgs mechanism: The Higgs proto-field (*) can be considered as an additional particle class to a Standard Model in which all of the other Standard Model particles are massless (**). It interacts with most of the other particle fields. But it also has a weird self-interaction which causes the energetically lowest state to not be at "no proto field" but at "some value of the proto-field". At low temperatures, where the Higgs proto-field is just lying around in its minimum, this means that the dynamic interaction terms of the Higgs proto-field with the other particles become some dull interaction of those particles with some sticky stuff that seems to lie around everywhere (***). In the mathematical description of the Standard Model time evolution, the associated terms that originally were terms of a dynamic interaction now become the mass terms for the other particles. If the minimum was at "no field", they would simply drop out (****). This "low-energy" limit actually covers almost all of the temperature ranges we can create on earth, and only recently did we manage to even create and see a few excitations of the Higgs proto-field around its minimum in specialized, very expensive experiments (-> confirmation of the Higgs-Boson at the LHC). So technically, I think we are very far away from creating the "massless particles" state in an experiment. But there is no theoretical reason why this would not be possible (*****). But as described, I would understand it to be less of a shielding of the Higgs field and more of an activation. And as a state with such a high amount of interaction between the fields. So I am not even sure if the common view of a few particles flying through mostly empty space and only rarely kicking into other free-flying particles would still make sense. Remarks: (*) I would just call it Higgs-field(s), but since the paper you cited seems to explicitly avoid using the name at this stage I may be wrong about common usage of the terms. Haven't been working in the field for over ten years. So I have invented the term proto-field for the scope of this post - it is also easier to understand than "doublet of complex scalar fields". (**) This is not exactly true because the particles are mixed and get renamed under the Higgs mechanism. But I'll pretend that does not happen for the sake of providing an answer that is easier to understand than reading a textbook. (***) Sidenote: In this state, the few excitations of the Higgs proto-field around its minimum are the infamous Higgs Boson. (****) Which is why you can always invent new fields that just happen to have no effect on anything we can see but magically make your particle cosmology equations work at very, very high energies (****) Except for the fact that some people still expect new physics and associated new particles at such high temperatures, which then again would have mass from another Higgs-like mechanism

I'm going to propose the opposite straight answer Time is a coordinate dimension akin to the known spatial dimension. Hence, you speak of the coordinates x, y, z and t or the coordinate tuple (x,y,z,t). Fields are functions that are defined on the 4-dimensional space described by these coordinates, written i.e. functions of type f(x,y,z,t) (or [math]\psi(x,y,z,t)[/math] or something similar if you prefer fancy greek letters).

As a side-note to the thread: The equation you are citing is the energy-momentum relation for a free particle. It is actually not called "Einstein's equation" (by physicists). The reason I am stressing this is because there is a different mathematical relation that is actually called "Einstein's equation", namely the relation between spacetime-curvature and spacetime-content. That doesn't invalidate your question, of course. For your actual question: I think zztop's answer perfectly fits what I'd have said. If you consider how important conservation of energy and conservation of momentum are it is only one step further to realize how important an equation relating energy to momentum can be.

The answer to your first question is: Not necessarily. If a, b, and c are real numbers and * is the multiplication of the reals then the statement is true. In case of vectors and the cross product a counter-example would be b = (1, 0, 0) and c = (0, 1, 0) where b is changed to equal (1,1,0). Since I assume that by "the momentum is not zero" you refer to the linear momentum then again the answer to your second question is "not necessarily". Take a radial vector (1,0,0) and a linear momentum (1,0,0). Changing the radial vector to (2,0,0) still leaves the angular momentum at zero. Your statement would work if the angular momentum was not zero, since scaling up the radial vector by a factor (while leaving the linear momentum constant) also scales up the resulting angular momentum by the same factor.

It is a bit hard to give a definite answer without knowing which parameters are given an which are not (your second paragraph suggests the mass of the bullet is given even though your first paragraph suggests it is not, for example). My guess would be the following: Collisions not only need to conserve energy, but also momentum. Additionally, the initial kinetic energy does not need to equal the final kinetic energy, since some of the original kinetic energy can be transformed into deformation energy. Hence, the kinetic energy of the bullet was larger than the energy of the resulting oscillation. Taking this into account (which becomes easy if, for example, you are given the mass of the block and the bullet) should give a correct answer, as far as I can tell.