can't_think_of_a_name

On 9/11/2020 at 5:56 PM, joigus said:

Where you write y, it should be (in standard notation),

 

γ=11−v2/c2−−−−−−−−√

 

Then you would have,

 

1−v2/c2−−−−−−−−√t′=t−vx/c2

 

 

1−v2/c2−−−−−−−−√x′=x−vt

 

It's Gauss reduction of linear equations from here quite straightforwardly. If you need more clues, tell me.

Edit: Maybe Gauss elimination is a more familiar name...

This post was made a while ago but I have quick followup question. Can gauss elimination or something similar be used in general relativity. I am not the greatest at solving equation like stated above. 

https://en.wikipedia.org/wiki/Lorentz_factor
 

Just scroll a tiny bit to find what I am referring to.

By L' I just mean L prime. I may have worded the title badly. Does the Lv/c^2 = L' ? Or can Lv/c^2 = L? 

When I was learning about the twin paradox I learned that in Bob's frame the space time diagram is represented by the diagram on the far right.
In Alice's frame the diagrams are represented by the far left and middle diagrams.
Doesn't this assume acceleration because there are 2 frames. How do I solve if there are no acceleration?  

https://imgur.com/a/mEaDPcP

Followup question. This is a psuedo paradox but why was this even deemed a paradox at first? Also according to the online class from courseara I am taking why did this confuse scientist upon first hearing it?

In S frame, why does the rope contract but not the distance between the ships?

There is mention of the ships and string not behaving as a rigid ship why?

I have been trying to the Bell's Spaceship Paradox but I am getting confused. Can someone simply explain the solution to the paradox according to special relativity?

https://en.m.wikipedia.org/wiki/Bell's_spaceship_paradox

Quote

Bell's spaceship paradox is a thought experiment in special relativity. It was designed by E. Dewan and M. Beran in 1959[1] and became more widely known when J. S. Bell included a modified version.[2] A delicate string or thread hangs between two spaceships. Both spaceships start accelerating simultaneously and equally as measured in the inertial frame S, thus having the same velocity at all times in S. Therefore, they are all subject to the same Lorentz contraction, so the entire assembly seems to be equally contracted in the S frame with respect to the length at the start. Therefore, at first sight, it might appear that the thread will not break during acceleration.

This is what I think I understand but I am not sure. This could be wrong.
The ships starts off the same speed 0v. Then the ships accelerate. Due to the Lorentz transform the ships distance gets longer. The rope also stretches. How does this lead to the rope breaking?
In the ships frame I see the ship the same length. I just see a person running. How do I reconcile the 2 frames?

Here is a good space-time diagram.
K is stationary person and K' is the moving ships

https://imgur.com/a/renojPE

https://www.physicsforums.com/insights/what-is-the-bell-spaceship-paradox-and-how-is-it-resolved/ (The picture comes from this link) 

Step 1 why is there only 1 "v" on the right?

Step 2 how do I remove the square root from "1-v^2 / c^2?" And how does "v + xt"  become positive?
 

Is there a latex guide to this site?

Do you know or have any idea where I can find examples of this difficulty of algebra to practice?

15 hours ago, joigus said:

OK. Let me know if you can follow the steps up to here:

 

v(t−vx/c2)+x−vt=v1−v2/c2√ t′+1−v2/c√ x′

 

 

(1−v2/c2)x=1−v2/c2√ (vt′+x′)

 

 

x=1−v2/c2 √1−v2/c2(vt′+x′)

 

OK? If you have any difficulty with that, tell me. There's one minor step left. And then the other equation. But if you understand this one, it's almost done. You can PM me, if you want.

I can't understand in step 1 how you get (gamma)x' and (gamma)t'. Doesn't the x' and t' start on the left side. I can either divide x' and t'  from the left side or - from the left.
Where did I go wrong?

Formatting incorrect.

1 minute ago, joigus said:

Arbitrary.

So I just plug in the values from the question?

15 minutes ago, joigus said:

Always break down problems into easy steps. Try a numerical example with say 3, -2, 7,... Get the idea. And then do it with a, b, c,...

Then go for powerful and general methods.

Once you get a solution, don't just be satisfied. Think: Does it make sense? If I make v=c, what do I get? What if I make v=0?

How does the equation of a light ray x=ct or x=-ct transform? Check.

I think I may have gotten x = -ct or something really similar. I just got confused because I don't know the value of x and t. What are the values of x and t? 

On 9/15/2020 at 2:16 AM, joigus said:

You don't need matrices. Look at my numerical example and try to understand what I did there.

In your OP case, it's v times the first equation plus the second equation, and vt -vt cancels and you're left with x in terms of t' and x'.

For the other one, it's c²/v times the 1st eq. minus the second. Now you've got cancellation x-x.Then there is some algebra left.

Gauss elimination with matrices is useful when you've got like 4x4 or even 3x3. But in a 2x2 system it's best to do it "by hand". 

I am having trouble solving the equation could you show the steps? Also do you have any tips when solving equations like these?

On 9/11/2020 at 5:56 PM, joigus said:

Where you write y, it should be (in standard notation),

 

γ=11−v2/c2−−−−−−−−√

 

Then you would have,

 

1−v2/c2−−−−−−−−√t′=t−vx/c2

 

 

1−v2/c2−−−−−−−−√x′=x−vt

 

It's Gauss reduction of linear equations from here quite straightforwardly. If you need more clues, tell me.

Edit: Maybe Gauss elimination is a more familiar name...

I drew the matrix as the image below. My biggest problem is I don't what to do next. I n the video it deals with a 4 by 3 matrix. I don't know how to apply Gauss elimination unless the matrix is 4 by 3. How do I apply it to different size matrices? I think I screwed up the matrix in this example.

I used this video. https://www.youtube.com/watch?v=eYSASx8_nyg

On 9/11/2020 at 9:42 PM, Endy0816 said:

This video covers it pretty well. You are likely already familiar with the matrices it involves.

https://www.youtube.com/watch?v=eDb6iugi6Uk

I don't know matrices but have been finding them quite easy to learn so far. What videos from the organic chemistry tutor should I watch to understand the video you linked.
So far I have watched

https://www.youtube.com/watch?v=yRwQ7A6jVLk

https://www.youtube.com/watch?v=vzt9c7iWPxs

Also what branch of math is matrices?

Lily's car has a fuel efficiency of 88 liters per 100100100 kilometers.

What is the fuel efficiency of Lily's car in kilometers per liter?

My initial reaction is to go   (8 L/ 100 km)  (?km/?L). The question marks just represent some variables in algebra. I just seem to drawing a blank what the numbers are. It is probably pretty obvious.
 

https://www.khanacademy.org/math/algebra/x2f8bb11595b61c86:working-units/x2f8bb11595b61c86:rate-conversion/v/dimensional-analysis-units-algebraically

I am using the link above to learn about dimensional analysis.

I don't know gauss elimination. What are the prerequisites to learn  gaus elimination? If I know the requirements I could just look up a video.

Consider the situation where we want to combine the space-time diagrams of Alice and Bob, where Bob is moving at a speed of 0.4c to the right (positive x direction). If we draw Alice’s x_A axis as horizontal and t_A axis as vertical, answer the following questions.(a) What is the equation, written in terms of x_A and t_A, that describes Bob's t_B axis (the world line where x_B = 0) on Alice’s diagram?

a) What is the equation, written in terms of x_A and t_A, that describes Bob’s t_B axis (the world line where x_B = 0) on Alice’s diagram?

I assume I want to change from Bob's  frame to  Alice's frame. Is this correct.

here are the relevant equation.

t' = y(t-vx/c^2)

x' = y(x-vt)

How do I transform from the equations t' to t equation? I.O.W I want the non primed time equation.

If I made any mistakes in my assessment of the answer correct me. Thanks.

I think I get it now.


I am just going to the do the math. t = d/v. t = 20.5  if memory is correct. Since Bob is moving I perform the Lorentz transform for time.  T = gamma(T' - (v/c^2)(x)

Gamma is = 7.14 if memory serves correct.

20.5 year  = 7.14 (T' - .99c/c^2)(20.3) =

T = 7.14 (T' -  20.1) =

T = 7.14( -20.1T' )

I think I made a mistake T' = gamma(T - (v/c^2)(x).

The mistake x = 0.

T = 7.14 (20.5 years) - .(99c/c^2)(0) =

T = gamma (T') =

T' = T /  gamma =

T' = 20.5 / 7.14 =  2.87

Is this correct?

Any further questions I will ask.

10 hours ago, swansont said:

If you want Bob’s numbers, you either analyze the experiment in his frame, or transform from Alice’s frame.

One thing we know is the answers will be different in each frame. In Bob’s frame, the trip will be about 3LY and consequently take about 3 years.

I think your comment and my comment state Bob always has to  be stationary. Is this correct?  Another member mentioned I should use rotate instead of twist. So since I rotate the graph XB = 0.  X_B is different to 0 compared to the non rotated graph giving a value different then 0. Is this correct? Or are you stating something different?

Let me clarify because my first situation was not explained well.

Please refer to the picture from imgur.

Find the time of Alice's clock when B reaches planet 2?
Find the time of Bob's clock when B reaches planet 2?

First question I think I understand . I just use d= vt  t = d/v
Second question.
Shouldn't the time of B = A? But I know this is wrong because moving clocks tick slow. Why do I have to perform the Lorentz transform when from my picture it shows it as the same time but I know the Lorentz transform must be performed because Alice is moving.

I think the answer is because I can only measure things in stationary frames and the Lorentz transform does this transform but also twists the graph . Since the graph is twisted during a Lorentz transform even if it is on the T_B axis  T_B = 0  isn't 0. Is this correct?

https://imgur.com/a/eWjTaT4

Should be X_A not X_B in Alice's frame.

Let's say I am in Alice's frame.Alice is located on earth. A planet called planet 2 is located 20.3 Light years away. Bob is on a ship that starts on earth and is travelling at a constant velocity .99c. Ignore the acceleration of the ship to get .99c Alice and Bob's ship's clock reads 0 when they reach earth.

Bob travels to the planet 2. Alice observers the time it takes for Bob to reach planet 2 using Alice's clock. What is this elapsed time?

Is the Lorentz transform only used during switching frames? Let me define switching frames. I may have a mistake in my definition. Please correct me if I am wrong. In this example I have 2 frames Alice and Bob. Alice is stationary Bob is moving.

I can calculate Bob's velocity in Alice's frame.

I simply do t= d /v. 20.3 / .99c = 20.5 years. This gives me the elapsed time.

If I wanted to know the time in Alice's frame.

Here is where I get confused.

I have a stationary frame. A moving frame I can switch between frames. When do I switch the stationary frame to become the moving frame, and the stationary frame becomes the moving frame?

When do I stay in the same frame but use the moving frame or the stationary frame?

What is the difference between the two previous questions?

Thanks.

These notes are from a class. How can this be wrong?

X_B is = 0.  Why do the gamma get crossed out?

Well I did say it may be a stupid question

This is isn't exactly homework help but I don't know where else to put it.

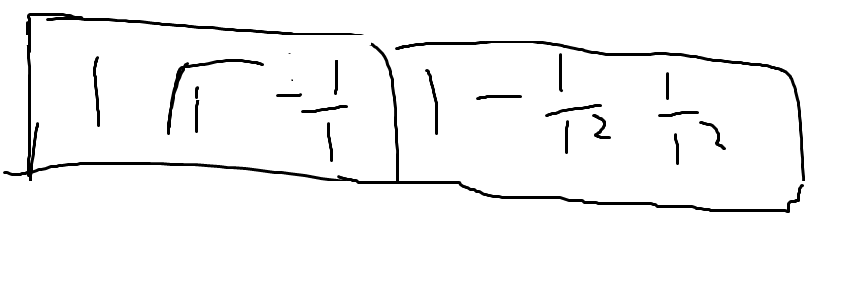
If A = 1 in this case and B is always = 1. Is it possible to get 1 instead of 0?

 1- A^2/B^2 = 0