rjbeery

11 hours ago, Markus Hanke said:

https://arxiv.org/pdf/1910.04372.pdf

I think the crux of the light trajectory around a Kerr-Newman black hole is showcased in this diagram.

If geodesics were to be strictly determined by time dilation this would imply that the field gradient is no longer strictly radial, but rather manifests as a spiral. Would you agree that this is possible, in theory? I'll investigate.

On 2/20/2022 at 4:11 PM, Markus Hanke said:

So if you can just acknowledge that your idea is useful in some circumstances, but limited in its domain of applicability, then we can be all good. After all, you can’t replaced a rank-2 tensor with a single scalar field (its 00-component), and expect to not loose any information in the process - that should make intuitive sense, no?

I acknowledge your point and appreciate your input very much. You'll forgive me if I remain skeptical. I need to find a scenario where the time dilation gradient cannot be used to determine the geodesic, and I don't think spinning mass qualifies. If light rays were to curve differently depending upon whether the mass was approached "with or against" the direction of spin then I do think that I would need to concede your point completely.

Let me think about it some more.

15 hours ago, Markus Hanke said:

But this isn’t what GR predicts - the geodesic in fact is determined by all components of the metric, plus boundary conditions. I thought you said your idea is meant to replicate the results of GR?

But in the frame-dragging scenario you provided the geodesics of light rays are identical regardless of direction around the rotating mass.

15 hours ago, Markus Hanke said:

Also, what exactly do you mean by “scalar time dilation field”? Time dilation is a relationship between clocks - so assigning a single value to each point in space isn’t enough, you need to also fix your reference clock somehow.

The reference clock is the Schwarszchild coordinate time of the infinite observer.

15 hours ago, Markus Hanke said:

The gradient only tells you direction and slope of change at each point, it doesn’t add any extra degrees of freedom.

I feel like you think my essay is trying to replace GR, but it's literally relying on GR to calculate time dilation and then using the gradient of that to determine geodesics. Geodesics alone to not describe everything about spacetime.

Place observer A inside a massive, transparent, hollow sphere, and observer B "at infinity" (with coordinate time). They will each claim to be inertial, with no local gravitational effects. Physics for both observers is identical because their local time dilation gradient is zero, even though the time dilation of observer A is higher than that of B.

The path of the light ray is determined by the gradient of the scalar time dilation field. It’s a vector. Frame dragging apparently does not affect the radial gradient of time dilation. Note that this if not the same thing as not affecting the time dilation field itself.

On 2/16/2022 at 7:41 PM, Markus Hanke said:

Well, you then have to acknowledge that in the general case, the kinematics of test particles depend on more than a single quantity.

It isn't a single quantity, it's a scalar gradient.

On 2/16/2022 at 7:41 PM, Markus Hanke said:

How does that work, exactly? Remember that it isn’t position that determines the difference in that example, but orientation (ie motion in direction of rotation, or against it). 

I'm not exactly sure what you're asking here, but frame-dragging is my response.

Quote

Rotational frame-dragging (the Lense–Thirring effect) appears in the general principle of relativity and similar theories in the vicinity of rotating massive objects. Under the Lense–Thirring effect, the frame of reference in which a clock ticks the fastest is one which is revolving around the object as viewed by a distant observer. This also means that light traveling in the direction of rotation of the object will move past the massive object faster than light moving against the rotation, as seen by a distant observer. It is now the best known frame-dragging effect, partly thanks to the Gravity Probe B experiment. Qualitatively, frame-dragging can be viewed as the gravitational analog of electromagnetic induction.

Anyway, as I said, different time dilation effects do not necessitate a change in direction. The straw will continue to appear to move "straight down" into a fluid, regardless of any change in index of refraction, because the surface of the fluid is perpendicular to the movement of the straw.

7 minutes ago, swansont said:

If you have a moving clock, it will experience time dilation. Even in deep space. Gamma is speed dependent in special relativity. 

I understand now. Yes, you are correct, time dilation (on its own) does not effect a light ray's path because it is the gradient that determines curvature. Even in an accelerated frame, where time dilation would exhibit a gradient, that gradient is in the direction of travel -- so, again, no curvature. We see the same thing when we stick our straw straight-down into the water; the index of refraction changes, but the path of light does not.

12 hours ago, Ghideon said:

I do not follow the physics of your argument, can you please explain? As far as I know gamma* is calculated using an invariant speed of light c. It looks lite you have an observer dependent speed of light, how does that affect gamma?

*) Reference: https://en.wikipedia.org/wiki/Lorentz_factor

The speed of light is taken to be invariant locally. If time is slowed down by 50% "over there" then the speed of light has also been slowed down "over there".

7 hours ago, swansont said:

In the scenario I brought up r would either be infinite, or is the same for both clocks, because we're discussing a situation where we're ignoring gravity. 

It's getting increasingly difficult to think that this is just an oversight on your part.

I'm sorry but I looked at all of your posts following my initial essay post, and I'm not sure which scenario you're referring to.

7 hours ago, swansont said:

So gamma is 1, from your calculation. There is no bending of light in deep space. And yet we can have time dilation

Yes. Have you looked at the diagram? Gamma is 1 at r = infinity. There is no bending of light in deep space; there is no gravity in deep space; there is no time dilation in deep space. I think perhaps you're mistakenly thinking about the meaning of gamma.

\frac{num}{denom}

On 5/30/2004 at 11:04 PM, Martin said:

testing

 

a′′a=−4πG3(ρ+3p)

 

 

ahhhh

$\frac{1}{3}$

[tex]\frac{1}{3}

good?

\begin{document}

\frac{1}{3}

23 hours ago, swansont said:

Why would the index equal gamma? I’m looking for a physics justification. Not something you’re just making up.

I have a full response, but I cannot get LATEX to work.

Here's the short, ugly version:

t_0 * gamma = t_r

where gamma >=1,  t_0 is the remote observer, and t_r is a clock at radius r above a large mass. For every second of t_r, the remote observer sees "t_0 * gamma" seconds pass on his local clock.

Now we take c_0 as the local (relative to the remote observer) velocity of light, and c_r as the velocity that the remote observer measures at radius r above the large mass. Velocity has time on the denominator, so we have

c_0 / gamma = c_r

where a local light-ray moves one light-second per second, but that same light-ray moves "one over gamma light-seconds per second" at radius r. This should make intuitive sense. If gamma = 2, then the clock at r moves half as fast; therefore light moves half as fast.

This gives

gamma = c_0 / c_r

which is the velocity of light "in a vacuum" over the velocity of light in another medium, which is the precise definition of the index of refraction.

1 hour ago, swansont said:

I don’t see how this relates to time dilation causing anything.

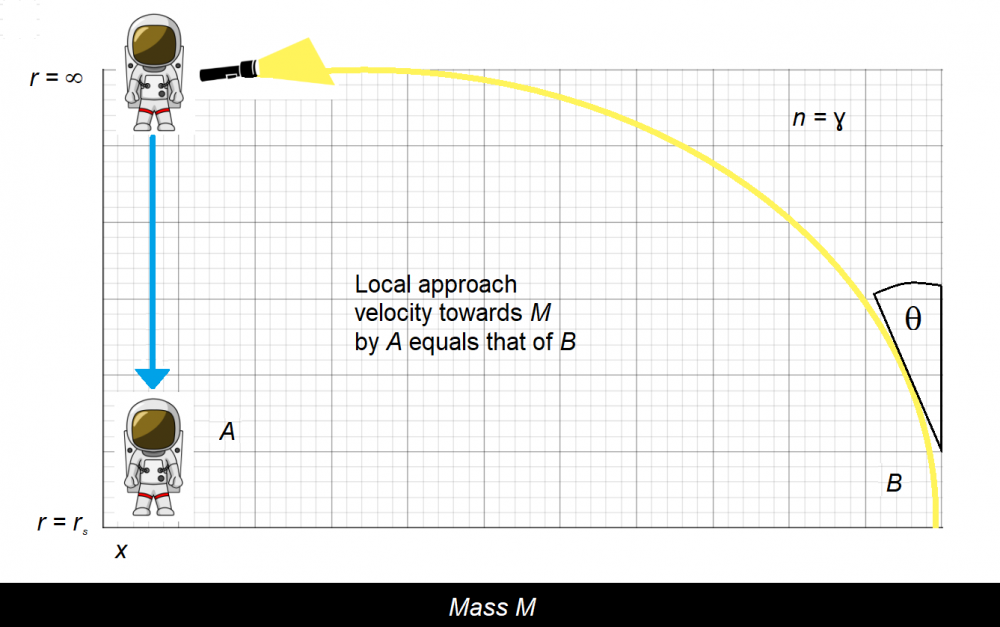
The light ray, B, isn't bending due to gravitational effects; it's bending due to the refraction index being set to the time dilation function. See "n = gamma" in the corner? B is approaching the mass M purely through optical considerations.

On 2/10/2022 at 8:15 PM, Markus Hanke said:

Suppose you have a rotating massive body of some kind. Further suppose you have two identical rays of light that pass this body in the equatorial plane, such that one passes along the central body’s direction of rotation, while the other one passes opposite its direction of rotation. The light rays are identical in all other aspects, ie they pass the rotating body at the same distance.

I gave this some thought. My response is that the gravitational potential may be the same for each ray, and the time dilation may be different, but it's the gradient that determines the optical path of each. We'd need a scenario where light rays take similar paths but move through different radial gradients.

14 hours ago, Markus Hanke said:

I have mentioned this further down - because the work done to go between points in the field must be independent of the path taken, or else the difference between those points cannot be a single unique quantity (=potential). This is how gravitational potential energy is defined - as a path integral between points within the field. If the value of this integral explicitly depends on the path, the definition becomes meaningless. This is true also in Newtonian theory.

Gravitational potential isn't even at the heart of anything here. For the falling body, A, I'm using PE + KE = constant as a shortcut to determine the free-fall kinetic energy as a function of r. The shell velocity could be determined in other ways. As for the light ray, B, I never refer to gravitational potential at all. GR time dilation is what determines the geodesic. Surely you'll agree that the GR time dilation field, as determined by an observer, is in fact a differentiable field?

12 hours ago, beecee said:

Any potential discovery, and/or improvement of GR will of course also need to run the gauntlet, so to speak, and not only predict and align with what GR says, but also add new observational verifications that GR does not.

I'm not refuting GR in any way. I'm showing a mathematical analogy between two disparate fields (gravity and optics) and suggesting that they are literally the same thing. This doesn't change any predictions made by GR, but it certainly could simplify mathematical treatments in it.

6 hours ago, swansont said:

members should be able to participate in the discussion without clicking any links or watching any videos. … Attached documents should be for support material only; material for discussion must be posted

I'm not sure why you would want to discuss a paper, or even raise objections to it, if you won't read it. That seems a bit combative to me. Nevertheless, the entire concept can be summarized in the following diagram.

8 hours ago, swansont said:

You said time dilation causes the refraction and now you’re saying it’s the other way. And without actually showing where time dilation is involved.

Poorly worded. The change in the velocity of light is caused by a change in the index of refraction of the traversed medium. A slowing of light is the very definition of time dilation. Did you read my paper? Because you made a vague remark implying that you did not.

17 hours ago, swansont said:

And how is that caused by time dilation?

It's time dilation caused by a change in the velocity of electromagnetic waves as measured by the index of refraction. Whether that cause is due to an abrupt change in the medium of travel, like vacuum-to-water, or if it's due to a gradual change in the medium of travel, like space-time approaching a large mass, is irrelevant. The math and behavior, both theoretical and in practice, are equal in both scenarios...and the presence of gravitational potential is not required. In other words, the change in velocity is (apparently) necessary and surely sufficient to display gravitational behavior.

12 hours ago, swansont said:

Well, I disagree, but in any event you need to address objections to your idea.

I'm not exactly sure what your objection is.

On 2/10/2022 at 10:57 AM, swansont said:

If you want to show something is causal, you need to isolate it from other possible causal effects. i.e. show that there are effects on light where time dilation occurs but where gravity is absent, or where you have a constant gravitational potential.

If this is it, then we take a glass of water in deep space (i.e. constant gravitational potential of zero) and stick a straw in it; the straw will appear to bend, and it's due to a reduction in the velocity of light in water.

14 hours ago, Markus Hanke said:

If such a potential exists, then the following boundary conditions must apply:

1. The spacetime is asymptotically flat

2. It is spherically symmetric

3. It is stationary

4. It is static

Why do you say this? Why would gravitational potential require those boundary conditions?

Off-the-cuff, I would say that movement in a direction opposite of a rotating body increases the corresponding relativistic masses of the respective objects. Increased time dilation should be expected.

I believe what you're submitting is that, even if the potential/refraction connection is correct, that gravitational potential cannot accurately describe expected gravitational movement in GR. Is that right?

1 hour ago, Markus Hanke said:

How do you explain these using Snell’s Law, and a single scalar field, respectively?

The gradient of the field is what curves the light ray, so scalars are not enough. I'll give your scenario some thought. In the meantime, perhaps you could look over the mathematics of the paper for errors (rather than the conclusion)?

2 hours ago, swansont said:

The ability to predict gravitational effects on light by applying Snell's Law to the graded time dilation field surrounding a massive object does not mean the implication is that all gravitational effects are purely the result of time dilation

Agreed, which is why I include this in the summary:

Quote

Parsimony and equivalence suggest that this mechanism is sufficient to explain gravitational forces on massive objects as well (possibly in one of the forms of EM mass in the literature [Bha07] [Wil97]).

If we can account for gravitational effects on light with time dilation, with a plausible reason to expect the same effects on massive objects, then it's bizarre to believe that there must be some additional mechanism (that is both identical and redundant to the time dilation effects), IMO.

2 hours ago, swansont said:

If you want to show something is causal, you need to isolate it from other possible causal effects.

I don't need to do that in this case. Snell's Law completely and perfectly describes the gravitational behavior of light. To suggest that there might be other possible causal effects on the light would mean that we're breaking the laws of optics as we know them.

The linked paper is an entry into 2022 Gravity Research Foundation's essay contest. I'm looking for criticisms and feedback. Basically, I show that we can predict gravitational effects on light by applying Snell's Law to the graded time dilation field surrounding a massive object; the implication being that all gravitational effects are purely the result of time dilation.

https://drive.google.com/file/d/1KsfgRHJvIYfm45NcJCKg6fGalDxp3QMJ/view

I've re-written this paper completely. Simplified for easier understanding, added diagram, bibliography, exported as PDF to make the look consistent. Looking for feedback. Thanks in advance!

https://drive.google.com/file/d/1KsfgRHJvIYfm45NcJCKg6fGalDxp3QMJ/view?usp=sharing

On 4/28/2021 at 3:55 PM, swansont said:

You know that I have not read the paper, so it is an ill-advised leap to say I agree to anything about it.

You've written far more in the discussion of this paper than what exists in the paper itself. I removed the Newtonian reference that offended you. At this point it's pretty suspect that you can't otherwise be bothered, but you've spent weeks explaining that fact.

On 4/28/2021 at 3:55 PM, swansont said:

You can’t physically realize an actually constant g. My position is that this doesn’t matter, at all, because physics solutions to idealized conditions are legion. Working with models doesn’t require physical realization, just no out-and-out violation of the relevant laws of physics.

Imagining a constant g is not the same thing as idealizing a frictionless surface. The former contradicts the theory, whereas the latter is ("merely") a practical impossibility. mgh is a first-order approximation, the same way 1/2 mv^2 is. We can use it for estimates, but we can't use it for making generalizations...particularly when the error in those generalizations is precisely tied to the terms we have excluded in our approximation.

7 hours ago, swansont said:

Time dilation may be defined this way under a particular set of assumptions such as having a spherical body of mass m, but one can't apply that in a situation where the assumptions don't apply.

Then we both agree that the paper is congruous with the implicit assumptions (e.g. spherical body of mass M), and any further objections would have to provide a set of assumptions for which these calculations don't apply.

In other words, we can both agree that the paper is self-consistent, and also that time dilation would occur under constant acceleration (but not vary under constant acceleration).

So, really, the only thing we disagree about is whether constant gravitational acceleration is a physical phenomenon, and I'm fine leaving it at that.

2 hours ago, swansont said:

That would seem to remove your objection to the fact that time dilation will happen in a region of constant g

Time dilation would occur for any general form of acceleration, but constant gravitational acceleration is unphysical. The high school shortcut of PE = mgh was superseded with the actual formula. Time dilation (gamma) is literally defined by r

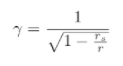
I think it's odd that my Newtonian reference offended you enough to not even look at the paper, but you're holding on to what we both know is bad math because you've apparently attached your ego to it.

On 4/23/2021 at 5:15 PM, swansont said:

I stopped when I saw you use 1/2mv^2 in a relativistic problem.

I've rewritten the first section to derive the relevant equation (eq. 5) without any Newtonian references.

On 4/23/2021 at 5:15 PM, swansont said:

Beyond that, you claimed that constant g will not cause time dilation or bending of light, which is blatantly wrong,

I could rewrite the equations to put the potential in terms of g but, as I said, I suspect you'll be dismissive. Therefore I found a full derivation that I doubt you can object to:

Relativistic Gravitational Potential and its Relation to Mass-Energy

On page 404, equation 54, the author seeks to prove that

Now that these objections are handled, do you have any other feedback? Because I'm going to be submitting this to a journal and I'm largely working in a vacuum.

Well, apparently Relativity and gravitational potential don't play nicely; something about being impossible to localize potential energy. It's been a long-standing problem that I'm only just reading about.

In any event, you shouldn't shut yourself off from what you may find to be very interesting:

https://docs.google.com/document/d/1RCmoSXd5YbkMHuYT8OwV_gW8uY5nl8BrBTELQevVfNE/edit

I'll come back to this. It should be as easy as putting potential in terms of g, although I'm not sure you'll concede the point, regardless.

In an event, have you ever seen gravity's behavior completely described in terms of refraction? Have you actually read the paper? Because that's what it does.