

Classical Physicist
-
Posts
33 -
Joined
-
Last visited
Content Type
Profiles
Forums
Events
Posts posted by Classical Physicist
-
-
force applied to a wheel F=ma
rolling friction is F=-μR
normal force R=-mg
Is that right?
going back to the Two-wheeled inverted pendulum that i have to find acceleration of, by using the point c that is the centre of mass of the whole vehicle,
how do I go about finding the torque at that point, which is on a line that is displaced at exactly the center of the rod that is in the axis of rotation of a vehicle… ?
I Really need to figure it out @studiot. I can't even tell you how much It would mean to me if we figured it out!
0 -
sure
But what forces do I need?
Torque at the point A, Rolling friction, normal force R, and …. force that is applied to a wheel?0 -
OKAY I need some serious help with it right now. What should I do to find this acceleration?
0 -
1 hour ago, studiot said:
See how simple it is ?
Following this example can you do the same for an individual wheel ?
Yes, It's easier to draw few FBD's for each of the wheels/ points, instead of making complex sketches full of informations…
Also what a cute car did You draw! - It's looks just like an Aston Martin! I will send Wheel FBD's here shortly. After this we should go back to finally analyzing the motion, right?0 -
1 hour ago, studiot said:
So what net forces are acting on the vehicle?
I'd say that the only net forces acting on a point C of a vehicle are
torque (2h mg sin θ )
force that gives us acceleration of a vehicle (2h ma cos θ )
and torque of a point C that is
τ=Iω
Image:
32 minutes ago, studiot said:I thought and hoped you knew better than that.
Sorry I've been trying to figure it out for days and I still have trouble with applying these forces in order to solve this problem, so I may have a flawed understanding of it right now.
As I understand "Rolling motion" is a sum of translational motion and rotational motion.
32 minutes ago, studiot said:You have stated no equation balancing forces here ?
Again no equations?
This one is the crux of the problem.
So you suggest starting with finding/composing some equations that will describe the motion of this vehicle? - Sounds correct. I'll see what I can do.
0 -
38 minutes ago, studiot said:
Do you know how to construct a free body diagram?
I think I can- but it's really not that simple when there's so many parts here to consider.
38 minutes ago, studiot said:Is the vehicle in vertical equilibrium (is it moving up or down ?)
It simply moves (accelerates uniformly with this unknown yet constant acceleration) in the right direction as the picture suggests. So it's not moving upwards/downwards- just rolling without slipping
38 minutes ago, studiot said:Is the vehicle in horizontal equilibrium (is it moving left or right ?)
we assume here that this motion is in the right direction of this horizontal plane. So I think we can say that the equilibrium is met here.
38 minutes ago, studiot said:So what net forces are acting on the vehicle?
This must therefore be the accelerating force on the vehicle.
Can you complete this ?
I don't see what you tried to post here- is it incomplete? Because you talk here about "the accelerating force on the vehicle"
38 minutes ago, studiot said:In your second diagram, what does the blue arrow ma represent?
I drew here a non-inertial case of this vehicle in motion - so ma would be the force that it takes to keep the motion going,
0 -
Okay so having all of these Drawn out, how can I find acceleration a that is at the point c which is centre of mass of a vehicle like this? @studiot, @Lizwi
And am I Missing some important factors here? - θ is the angle that the pink/black rod moves from the equilibrium position that is on the normal line to the surface in order to accelerate a vehicle- something like a segway/ moving inverted pendulum.Thankfully we can omit the rolling resistance - (forces that make the vehicle decelerate) But torque for a point C would have to be a sum of torques acting on this point - right?
And from here we would make some equations and transformations in order to find the acceleration a?0 -
-
Let's picture a Rolling without slipping Wheel, that constantly accelerates. radius of a wheel/circle is rr.
Basically any wheel of a vehicle is rotating around its fixed axis - AoR -(axis of rotation)
Most of the times wheels have this AoR perfectly in the center of the circle/wheel/cylinder. What I want to understand is how can we describe the torque of such a wheel?
Because as I understand we could go about finding torque for the center of the circle - point O.
I am not sure if it's possible to find the torque for the point P, that is point on a line tangent to the circle on the surface level.
0 -
On 10/7/2019 at 11:57 PM, studiot said:
d(flux)/dt gives an induced voltage (with a sign)
So putting this into mathematical form
dΦ=−BdA
divide both sides by dt
dΦdt=−BdAdt
Where A is the area enclosed by the (triangular loop)Faraday's law.
E=−dΦdt
Where is is the voltage generated in a wire at right angles to the fieldNow draw some positions of the blue wire in at varous times.
Also extend the velocity vector of the blue wire in both directions.What do you notice about the triangular areas so formed?
Can you connect this to the above in terms of the velocity of the blue wire?
The point of the similar triangles is that you don't need any actual values of area, ratios will do.
One further note.
E is generated only in the blue wire because it is the only wire moving.
The black wire is stationary in the field so no voltage is generated in this one.
The circulating current in the loop is entirely due to the motion of the blue wire.
One final twist - is the blue the blue wire motion at right angles to the field, in accordance with Flemings rule?
oh I forgot about it so I got this:
is this correct?
0 -
@studiot I guess I have to yet find the third period that is of the overall system so (0.867+1)/2 = T3 That is 0.93?
0 -
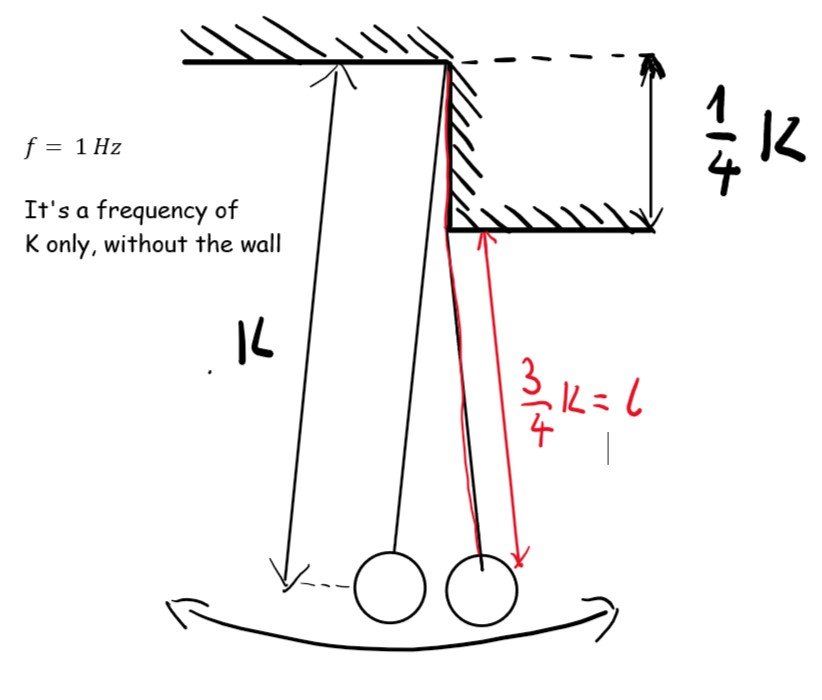
hey It's me again, I need Help with this pendulum problem,
it is easy :
The frequency of vibrations (fluctuations) with a small amplitude of the ball
attached to a weightless string is 1 Hz. I have to find the frequency
of small vibrations of this body suspended on the same string near the edge
shown in the picture. The distance d of the edge from the suspension point is 1/4 k.it's easy but i have trouble with comparing it to the "seconds pendulum"
Because with seconds pendulum we get frequency f= 1/2 Hz.
but here we have
so can we compare the two periods like this?
so plugging these in I got this:
is this correct?
0 -
Love it, Thanks again, I'll post the further answer shortly, …. so how can I insert the maths in here? beause I tried with LateX syntax but it didn't output this nice formatting that you post here?
0 -
12 minutes ago, studiot said:
https://byjus.com/maths/area-of-similar-triangles/https://byjus.com/maths/area-of-similar-triangles/
You will need both lengths and areas
I'm confused
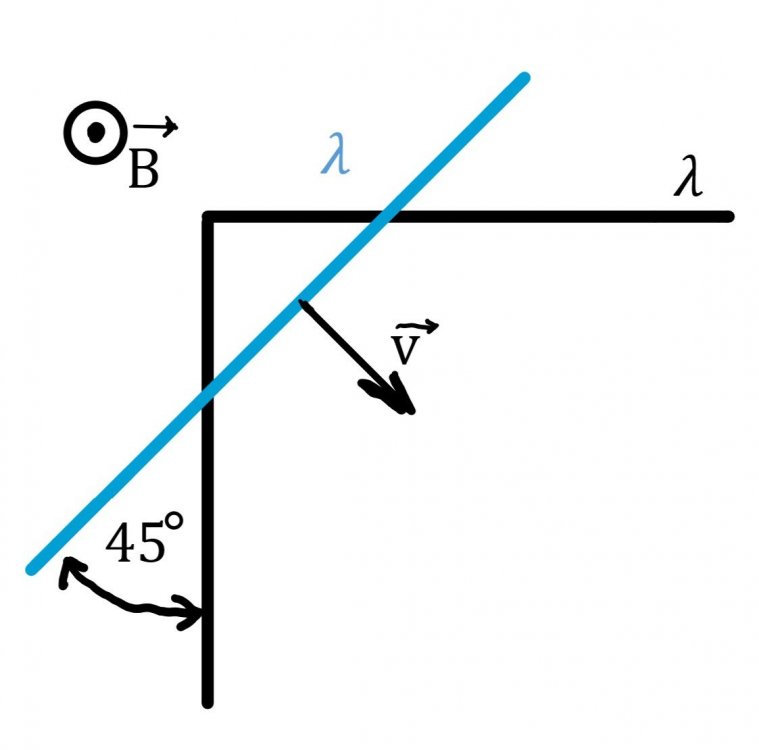
The “height” of the triangular area enclosed by the underneath wire and the one above is the same as the distance traveled in time v: d = vt, also the base of the triangle like that equals to λ
(as in picture)
so we get
1/2* λ*vt=ADo I understand correctly that λ is the length of the wires? - in which case the bent one has λ as a sum of these "sides",so that each side is λ/2?
however geometric look at the picture denies that- so the bent part would be 2λ, 1 λ for each side, just like the moving wire above, with l=1 λ.
38 minutes ago, studiot said:https://byjus.com/maths/area-of-similar-triangles/https://byjus.com/maths/area-of-similar-triangles/
You will need both lengths and areas
I still don't get which exact triangles should I take into consideration, I mean I understand these ratios, but which triangles with an angle of 45, 45 and 90 from the problem do I need, exactly?Never Thought that I would have to ask you about such trivial stuff, but hey I am very tired right now… However that is still not an excuse.
0 -
8 minutes ago, swansont said:
IIRC there are problems like this in Halliday & Resnick (and no doubt in the later versions) with a square cross-section. Making it a triangle just adds a little extra geometry to the mix.
which chapter is it? the 28th - with magnetic fields, right?
Actually the 30th chapter about "Induction and Inductance" is more accurate here, --- you're right the problem 18 from the chapter 30 looks quite similar.
0 -
I just got back from Uni and had not much time to sit down to it. But It also boils down to be quite much easier than it appears to be- For a while I was thinking about the whole physics that we could use here, but still your problem solving techniques - about the geometry are still a bit "magic" to me, I get them but, intuitively I would have to practice more to see these just like you do,
So the geometry and similarity are well-known to me (or so I suppose), but as you suggested we need to focus on the moving wire that geometrically makes up a triangle with the other wire underneath it. - I sense some differentiation that has to be done with it?we basically have a function of time (?) that with the upper wire movement makes up for an increasing area of a triangle with angles of 45° 45° and 90°.
which as time passes by --- reaches the point where the sides are just like in a special triangle with angles like that.0 -
55 minutes ago, studiot said:
So where did this question come from and why are you doing it?
I found it online maybe ...half a year ago, don't really remember the origin of it, it was from some script or notes from/for students of the first year of some course on physics from A university I don't ever so slightly have an idea of (not sure though) that I found while looking for something that could help me understand the electromagnetism better? I don't remember, and the problem was handwritten so yeah, I just got down what you see here.
0 -
1 hour ago, Enthalpy said:
The way I understand it, the bent wire is immobile versus B while the skewed one, of identical nature, moves and is in contact with the bent one.
d(flux)/dt gives an induced voltage (with a sign) while the summed wire length gives a resistance. Neglecting the self-inductance (="the field produced by the wires themselves") you get a current.
Note that 8T is unusually strong. It take a superconductor or a small duration. 32ohm/m is much even for a resistor wire.
Yes you're right- that's what it is. two electrical conductors (in a form of wires) with the identical nature.
0 -
So I think I need to use the faraday's law here to solve it?
0 -
for now I'll have my physics problems posted in "homework help" - because the moderators don't like threads like these in this subtopic
0 -
I have a hard time understanding the latter of it- how come the same wire slide upon itself with a velocity, while being inside the magnetic field B?
The way I see it- these might not actually be 100% same wire, rather two distinct wires, with the same properties, but being separated? -
HOWEVER it wouldn't make sense then, because we need to find the current I, (that is supposedly the same in each "part" of the "wires")…
So that is maybe a wrong assumption to begin with.So coming back to the idea of the same wire sliding upon itself - we need to take a look at the basic electromagnetic properties in order to push the problem further?
4 minutes ago, Strange said:!Moderator Note
Moved to Homework Help. Please show how far you have got
huh, I was going to just do that right now, because I didn't want to clutter the thread, but hey.
 0
0 -
A wire with resistance per unit length of 32.668 Ω/m is bent at a right angle. The second straight fragment of the same wire (The blue one) moves at the top of the first one at a speed of v = 4.2735 m/s. The whole system is located in a magnetic field with an induction of B = 8.4965 T, perpendicular to the wires (as in the picture). Determine the current flowing through the wires. Ignore the resistance at the points of contact of both wires and also the magnetic field generated by the current itself that is taken into consideration.
0 -
21 minutes ago, studiot said:
Yes wheel out your extra ordinary problems, but one at a time please.
A final question,
Do you understand significant figures?
We only know g to 3 s.f.
So there is no point recording more than 4 sf in the calculations for the values of other quantities.
I'm so grateful, for your help, I really get to understand the physics on so much deeper level now as the time goes on, I'll post some more problems in new threads, but as You said -one at a time! Also yeah I Get the significant figures. - so for
T=0.40452441211872491886336935537142 s
we simply get t=0.405s ,:)
0 -
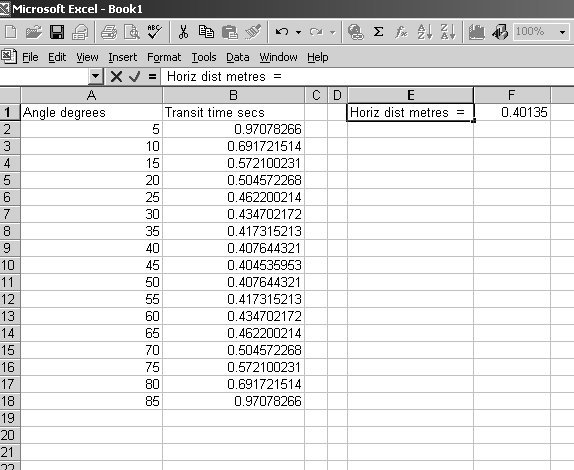
1 hour ago, studiot said:
Here is an excel spreadsheet at 5o intervals
Yes it gets a bit messy but not too much.
Did you understand the use of the double angle formula?
sin 2θ = 2sinθcosθ
I was recommending the book to you as you can see from its fron cover, Levi sets out to do physics instead of maths and develops some fascinating and ingenious ways of connecting well known Maths theorems to the physical world.
I though you would be interested.
The only part of the extract is the picture moving the pole round the corner.
The rest of the text is not relevant.I have uploaded the spreadsheet by adding .txt to it
To return it to xls, remove the final .txt and you can play with other values
The base distance, b, is input into box F1 so it can be changed for other distances.
Huge thanks for making a spreadsheet, - so now for sure the sin(45) gives the answer I was looking for. And yeah, I understood the use of double angle formula there, too - a smart way to use it in these type of problems, and I also got the book, and Will certainly have a look, ...explaining calculus problems with some physics sounds very promising!
I have some other quite "extraordinary" problems to go through, would you also like to take a look at them?
 0
0

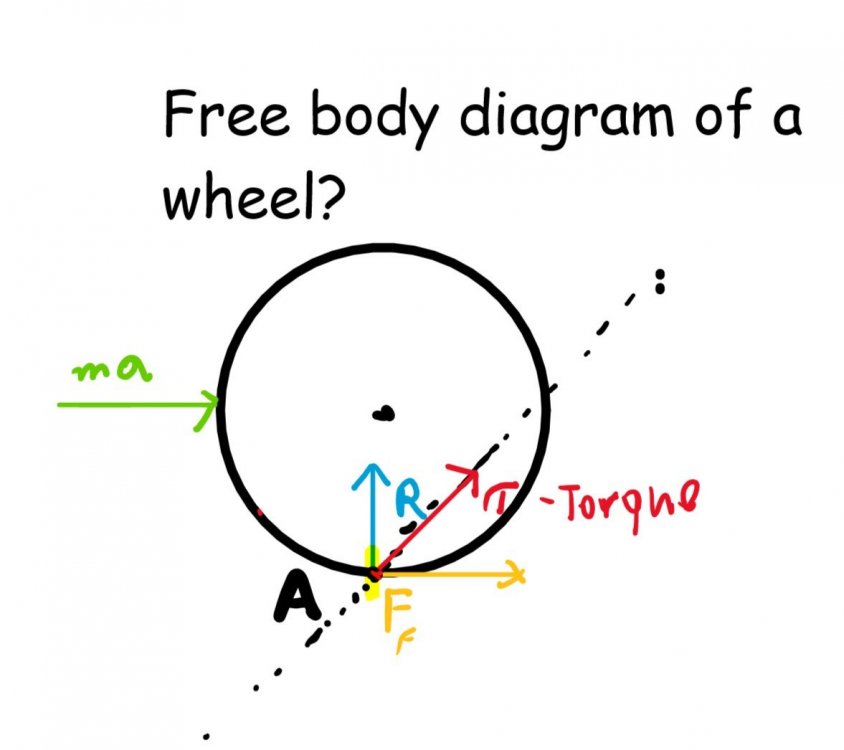
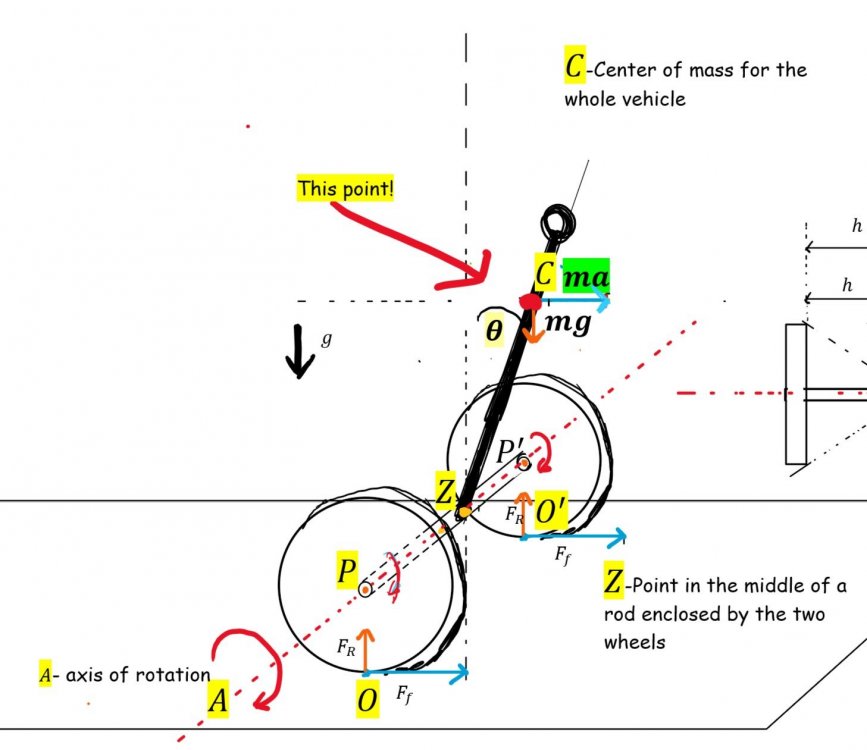
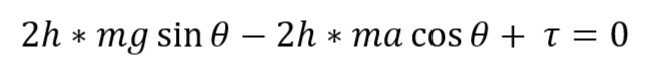
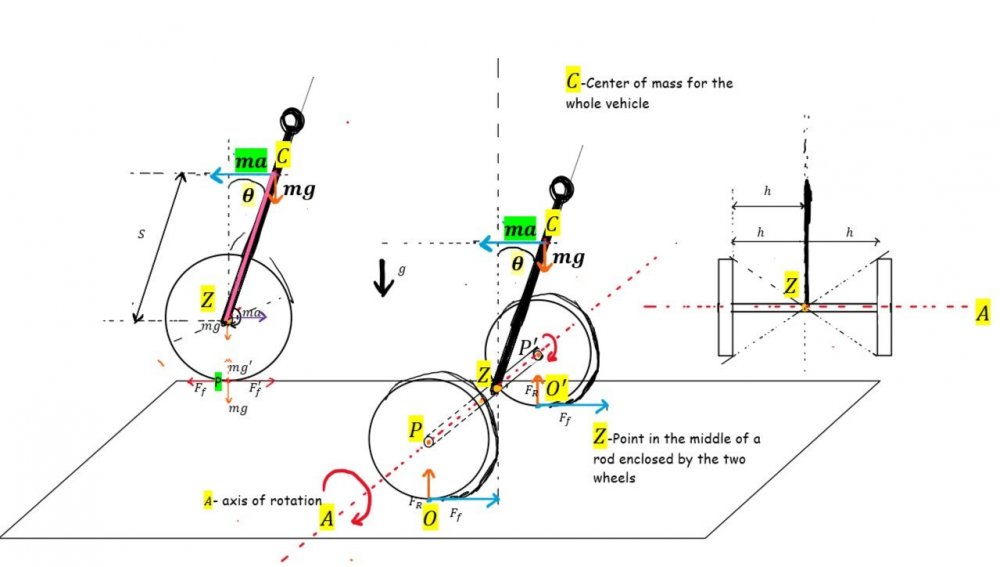
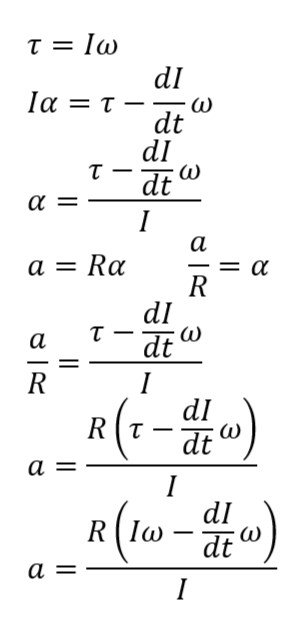
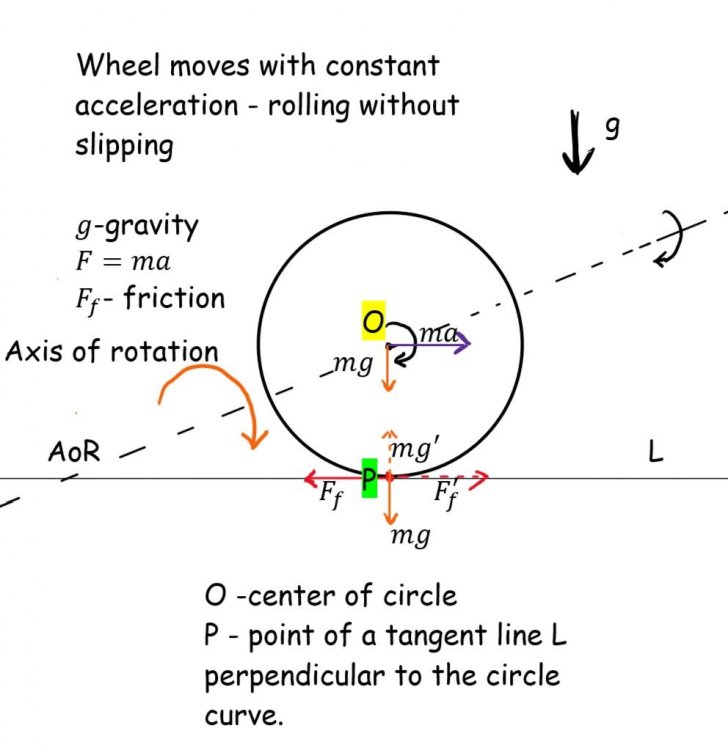


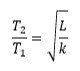
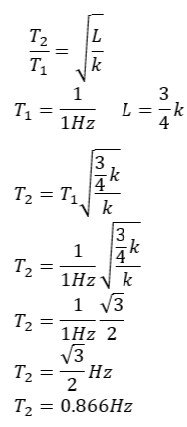
What is torque, really? Can it be determined for a point on a circle that is away from the center of the rotation axis by a radius “r”?
in Classical Physics
Posted
ok so rolling friction is just F= μR