

mathspassion
-
Posts
46 -
Joined
-
Last visited
Content Type
Profiles
Forums
Events
Posts posted by mathspassion
-
-
On 6/2/2018 at 10:17 PM, Bignose said:
then, mathspassion, you need to go and learn some algebra. Because the 'proof' is simply variable manipulation.
If your namesake is true, and you have a passion for maths, you should be trying to learn as much of it as you can. And algebra is a very fundamental building block of math.
Not only that, but if you learn algebra, you'll be able to express ideas -- like the one that started this thread -- into a more succinct and generally understandable format. Strange was not the only one who struggled to understand what you were trying to say. Learning the terminology and nomenclature that you will learn in algebra will help you convey your messages much, much easier. It is worth the effort.
For your namesake bignose do not try to tell me know algebra my dear I know very well first you read all the quotes then write dear after reading few quotes u are not suppose to write anytning anywhere ok
-3 -
16 hours ago, Strange said:
Aha! Got it. It makes sense now.
And, (sorry for belabouring this, but it has taken me all this time to understand the original post!) this explains 4 (N - 1) + (N - 2)^2 = N^2.
Using (Ath Sq. on X-Axis) * (Bth Sq. on Y-Axis)" = (A+1)*(B+1) we can see that:
[(N-2)th Sq. on Y-Axis] * (3rd Sq. on X-Axis) = (N-1) * 4
[(N-3)th Sq. on Y-Axis] * [(N-3)th Sq. on X-Axis] = (N-2) * (N-2)
So the OP's equation for N2 = (N-1) * 4 + (N-2) * (N-2)
And we are back where we started.
thnxs a lot for sense now but to be very frank as you related the formula with N2 = (N-1) * 4 + (N-2) * (N-2) that,s i do not know but how this formula N2 = (N-1) * 4 + (N-2) * (N-2) came into existence I know I have proved two formulas for cube or square through points on pyramid .ok it,s happened all of a sudden when i was working on straight line divided into same ratio got another line again divided into same ration till i got the one point then the miracle happened and got amazing results.
For kind information i never manipulate formulas .... for every formula i have the basic concept from wher and how this formula i got. ok.
thnxs for quoting and keep continue
17 hours ago, uncool said:Strange - it doesn't mean max. It means number of lattice points in a rectangle with the two given dimensions. This gives the formula "(Ath Sq. on X-Axis) * (Bth Sq. on Y-Axis)" = (A+1)*(B+1). For example, mathspassion, am I correct in saying that (2nd Sq. on X-Axis)*(4th Sq. on Y-Axis) = 15?
I don't know what you mean by "how this formula came into existence"; I have provided a geometric proof (or at least, the summary of one), which is what you asked for.
I have proved and have proof of this formula which you mentioned and two more too. o.k dear.
0 -
17 hours ago, Strange said:
The proof is:
(N-1)(4) + (N-2)(N-2)
= (4N - 4) + (N-2)(N-2)
= (4N - 4) + (N^2 - 4N + 4)
= 4N - 4N - 4 + 4 + N^2
= N^2
QED
dear it is very simple but do you know how this formula came into existence if not in the next quote i will define you i have already proved through points .o.k wait for.......
16 hours ago, uncool said:To see it more geometrically, you can see the (N - 2)^2 as a square in the center of the N^2 square. Then you can divide up the "border" into 4 parts. Each will have N - 1 points.
dear it is very simple but do you know how this formula came into existence if not in the next quote i will define you i have already proved through points .o.k wait for.......i have done lot work on (more then 20 years).
-1 -
12 hours ago, Bignose said:
Dude. Just multiply it out. This is like basic algebra. Post here if you need help, but if you just expand each term on the right hand side, you'll see the terms cancel and prove the identity.
ok we know dear but there must a proof and prove ok.
-1 -
20 hours ago, Strange said:
Don't bother. I don't watch videos. (They are the worst possible way of explaining things.)
If you can't explain it here in a few sentences, then this is obviously such an impossibly complicated process that it isn't worth spending any time on.
verrrry strange neither mention you mail nor want to see on youtube and saying it is very complicated process something wrong with you as you already mention in your first quote it is complicated process means you already have read example then you replied and in trolling quote you trying to say it is complicated complicated and complicated what is this ............dear Strang my suggestion is to you always appreciate others work .............do not try to down others. ok
19 hours ago, uncool said:If I'm not mistaken, this is a rather long assertion of the fact that for any N,
4 (N - 1) + (N - 2)^2 = N^2.
first time i am seeing this formula i am not aware of it i was just working on X-Y AXIS and got that results you know everything is related with each others if it is not we can not prove and proofs things ,ok .
maths is the only subject where we use x y for example x+y=24 xy=12
ok ....take care
16 hours ago, uncool said:The idea was that the * the OP was using denoted the largest number gotten when labeling the vertices of a lattice inside a rectangle of the two given side lengths. So the 3rd square *3rd square denotes the largest number gotten when labelling the vertices of a lattice inside a 3 by 3 rectangle, as shown in the picture. But once we have that, it's not hard to see that that is equal to (A + 1)(B +1), where A and B are the "number of squares". So, translating the formula, we get N^2 = (N-1)(4) + (N-2)(N-2).
can you prove this formula
N^2 = (N-1)(4) + (N-2)(N-2).
-1 -
1 hour ago, Strange said:
Of course not. Just post the steps here.
Just explain how you "count the nos of dots(points where crossing with each others)start from origin to 3rd square to 7th square"
I assume this will just take 3 or 4 sentences.
ok in few days I will quote a link(youtube) in which every thing will be clear ok...............but i am so surprised not mentioning your email address, it is gr8 wow ......is there any problem .......
0 -
On 5/26/2018 at 9:37 PM, Strange said:
Or let me try... start from origin to 3rd square to 7th square : OK, I start from the origin, count to the 3rd square (on Y, presumably) that is 3, then I count across to the 7the square (on X) and that is another 4. So I make that 7 total. Or, if I multiply them, 12.
Maybe I am being very slow, but I don't get it.
You are obviously counting them in a different way. Can you explain how?
Also, why do you say "count the nos of dots(points where crossing with each others)start from origin to 3rd square to 7th square"? What happened to the "7-2th" square?
If you don't want to explain, I'll just have to give up trying to understand it.
sir no i will sure try to explain it in wide if u do not mind........ may u pl mention your email or whatsup no so that i ping u or email u the link ok
0 -
3 hours ago, Strange said:
I can't follow your examples. Can you show how you get from: (7-2)th(3rd squ) +(7-3)squ.(7-3)squ to 24 + 25
Presumably, (7-2)th(3rd squ) = 24 ?
But why?
What is (7-2)th and what is (3rd squ) and why?
very strange and very simple why do u not try to understand ... in your first quote u wrote it is very complicated it means u have read all the things with example now what u want to ask i am unable to tell u ...
now (7-2)th means 5th square ,(3rd squ) mean third square now count the nos of dots(points where crossing with each others)start from origin to 3rd square to 7th square.ok
dimag per jor lagaooo........
0 -
On 5/24/2018 at 3:51 PM, Strange said:
There is no value in the 5th(at y). Or are you not using the numbers in your grid? If not, I don't understand what you are doing.
What do you mean by "count the nos of points"?
Perhaps you need to show a complete example; i.e. all the steps not just the first and the last.
sir very strange have u not seen the two examples .......................... example also quoted of 5 and 4 .
0 -
On 5/22/2018 at 3:41 PM, Sensei said:
4/3 = 1.33333333(3)
5/3 = 1.66666666(6)
1 + 1.33333333(3)^2 = 1.66666666(6) ^2
1 + 1.777777777777777777777777777777(7) = 2.777777777777777777777777777777(7)
also:
(4/3)^2 = 16/9
(5/3)^2 = 25/9
9/9 + 16/9 = 25/9
what u write we all know my question is up to how many decimals.......o.k. why not trying to understand.
0 -
20 hours ago, Strange said:
Well, I'm not quite sure what you are doing there (you seem to have skipped some steps). But as far as I can see, the (7-2)th square (i.e. the 5th square) is empty.
So, when you write "(7-2)th(3rd squ)" how do you get from there to "24"?
very easy 5th(at y) square to 3rd squ(at x) count the nos of points u will get 24.
9 hours ago, Bignose said:So... you've converted 1 number lookup (the N) and 1 multiplication (N*N) into 4 number lookups (have to find the numbers on the square snake thing), 2 multiplications, and 1 addition. I guess I fail to see any practical reason for it, tho that has been said about a lot of math.
sorry no any converted.............. it is very hard to get formula ......................I took years to get it. It is not a Manipulation dear.
Dear Bignose ...........Very simple to write anything(there is something wrong with peoples) but when u do something new it takes time and lot hard work .
0 -
It seems like a very complicated way of calculating squares.
And it will inly work for numbers up to 7, if I understand it correctly.
yes complicated but a new way on X-Y Axis why u saying it will work up to 7 pl explain.square of 7
as per formula
(7-2)th(3rd squ) +(7-3)squ.(7-3)squ
24 + 25=49
0 -
Square Through Squares

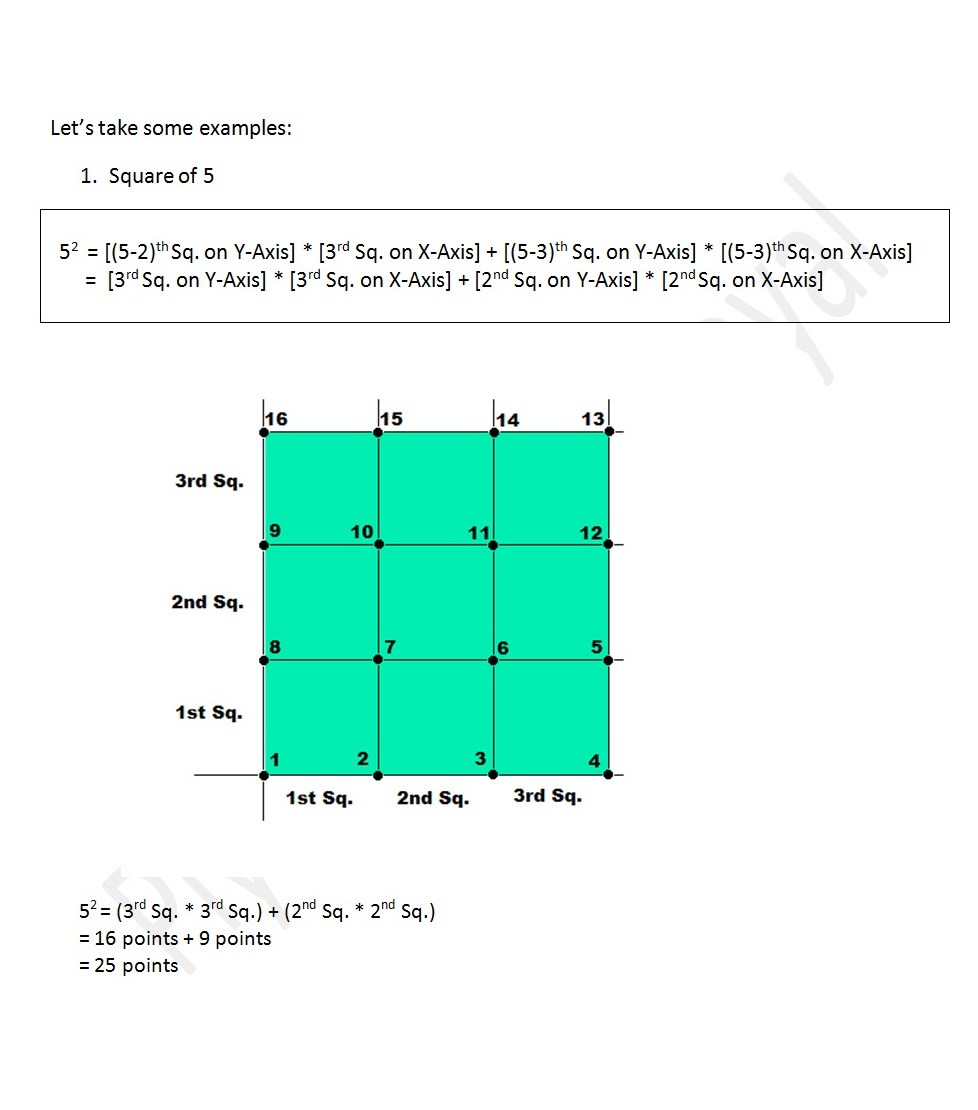
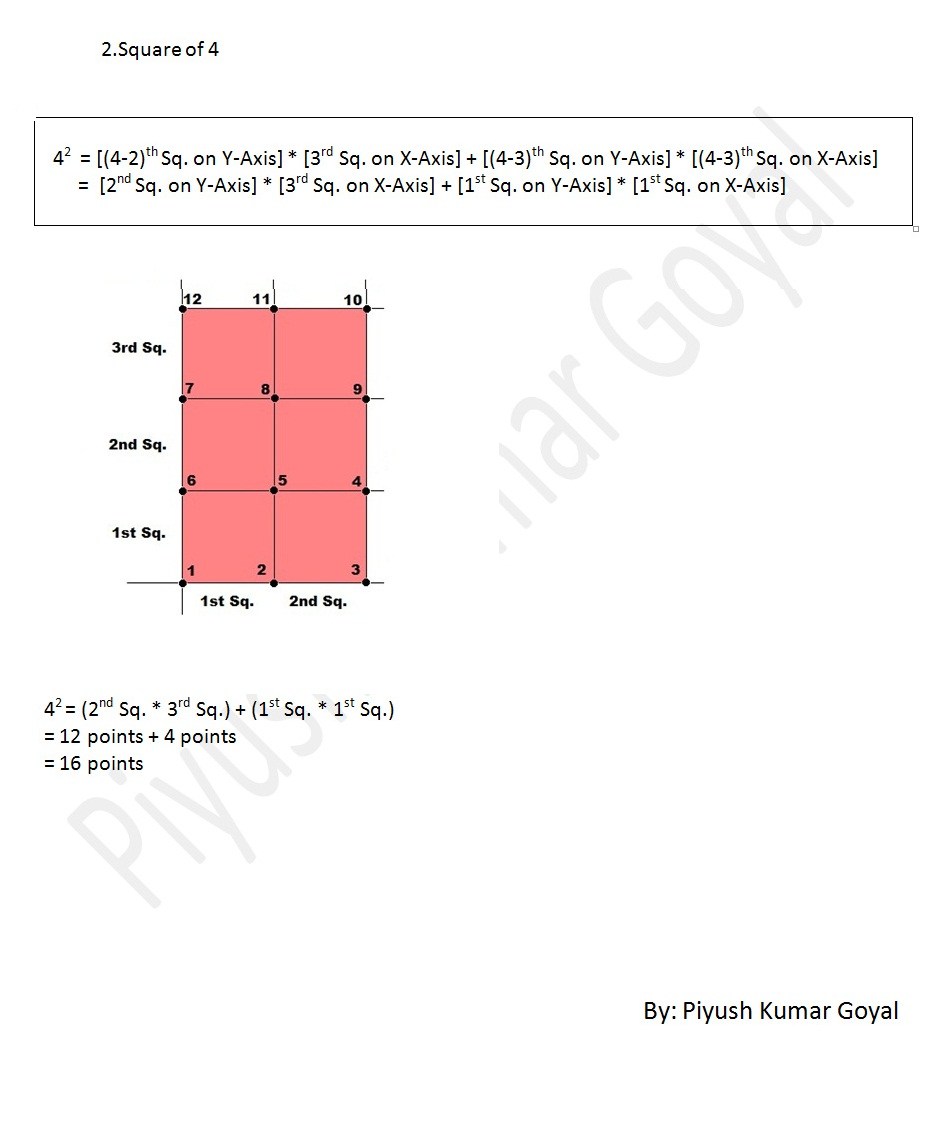
Copyrighted©PiyushGoel
0 -
Accuracy up to how many decimals...........?

32 + 42 = 52
9 + 16 = 25
1.(3/4)2 + (4/4)2 = (5/4)2
0.752 + 12 = 1.252
0.5625 + 1 = 1.5625
2.(3/5)2 + (4/5)2 = (5/5)2
0.62 + 0.82 = 12
0.36 + 0.64 = 1
O.K. Fellas, let’s notice a difference here.
3.(3/3)^2 +(4/3)^2 = (5/3)^2
1^2 + 1.3^2 = 1.6^2
1 + 1.69 = 2.56
Difference => 2.69 – 2.56 = 0.13
Accuracy =>0.13/2.69=.048
4.(3/3)^2 +(4/3)^2 = (5/3)^2
1^2 + 1.33^2 = 1.66^2
1 + 1.7689 = 2.7556
Difference => 2.7689 – 2.7556 = 0.133
Accuracy => 0.133/2.7689 = 0.0048
5.(3/3)^2 +(4/3)^2 = (5/3)^2
1^2 + 1.333^2 = 1.666^2
1 + 1.776889 = 2.775556
Difference => 2.776889 – 2.775556 = 0.001333
Accuracy => 0.001333/2.776889 = 0.00048
6.(3/3)^2 +(4/3)^2 = (5/3)^2
1^2 + 1.3333^2 = 1.6666^2
1 + 1.77768889 = 2.77755556
Difference => 2.77768889 – 2.77755556 = 0.00013333
Accuracy => 0.0001333/2.77768889 = 0.000048
7.(3/3)^2 +(4/3)^2 = (5/3)^2
1^2 + 1.33333^2 = 1.66666^2
1 + 1.7777688889 = 2.7777555556
Difference => 2.7777688889 – 2.7777555556 = 0.000013333
Accuracy => 0.000013333/2.7777688889 = 0.0000048
8.(3/3)^2 +(4/3)^2 = (5/3)^2
1^2 + 1.333333^2 = 1.666666^2
1 + 1.777776888889 = 2.777775555556
Difference => 2.77777688889 – 2.777775555556 = 0.0000013333
Accuracy => 0.0000013333/2.777776888889 = 0.00000048
So, as you can see its pretty much visible here that irrespective of the precision there is in division, the presence of digits 4 and 8 in the Accuracy Factor is mesmeric to look. This may come under Number Pattern Theory where the operation eventually leads to same numerical digits though quantitatively they are different.
Author: Piyush Goel
0 -
21 hours ago, studiot said:
What would you expect us to say?
Congratulations you have derived the conventioanl formula for the area of a trapezium as being the average length of the parallel sides times the perpendicular distance between them.
Incidentally I would check the first line of your proof for what I assume is a typographical error.
BCEG is not a triangle as stated. Also the letters are not in cyclic order round the square.yes right BCGE is not triangle it is square and second letters not in cyclic order ....sir thnxs a lot for mentioning two typographical error........next time ....never .
0 -
oh! very nice to see............. there is no comments .................wonderful.
-1 -
How to get ,The Area of Trapezium from Triangle
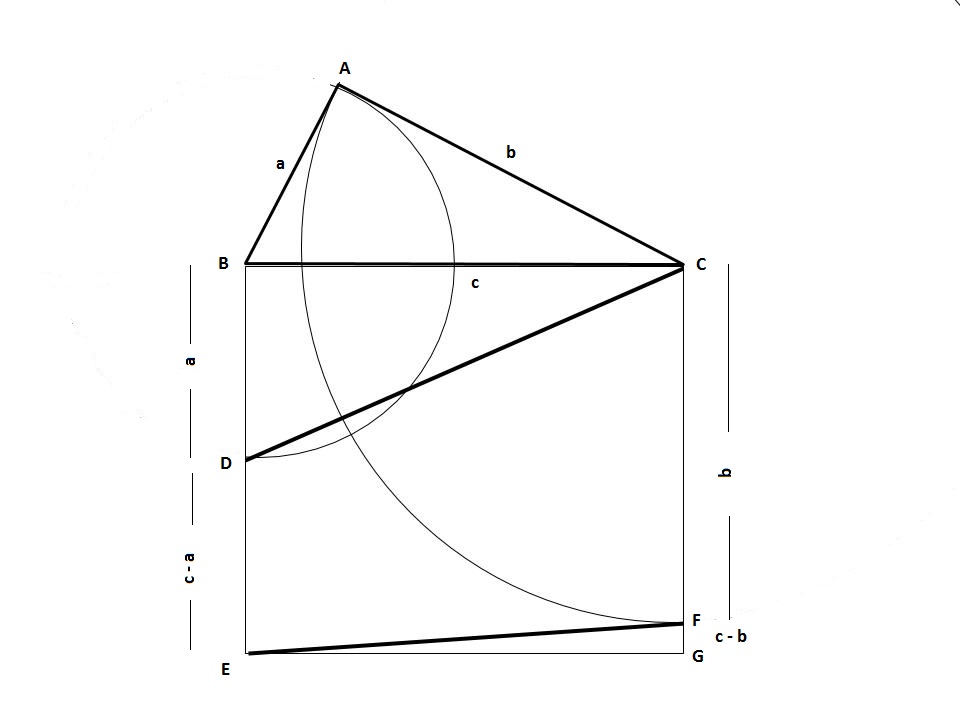
Lot of mathematicians have proved Pythagoras theorem in their own ways. If you google it you will indeed found hundred of ways.
Meanwhile I was also sure that maybe one day I could find something new out of this incredible Pythagoras theorem and Recently I got something which I would like to share with you.
To Prove: Deriving the equation of area of trapezium using Arcs
Proof: There is a triangle ABC with sides a b and c as shown in the figure.
Now,
Area of ∆ BCEG = Area of ∆ BDC +Area of ⌂ DCEF + Area of ∆ EFG
c^2=ac/2+ Area of ⌂ DCEF + (c-b) c/2
(2c^2– ac –c^2+ bc )/2=Area of ⌂ DCEF
(c^2– ac+ bc )/2=Area of ⌂ DCEF
c(c– a+ b)/2=Area of ⌂ DCEF
Area of ⌂ DCEF=BC(DE+CF)/2
Copyrighted©PiyushGoel
0 -
hello appreciate someone work .................
0 -
I do not know how the people discourage one,s attempt ,well done keep it up DO IT IN DETAILS.....
I know few people ................( habit of Barking).....
like andy pendy.....
-2 -
Respected All
Everybody knows this work done years ago the man who created this i think he also understand......
why all of u try to down creative man work....
1. if he has done something new appreciate his work.
2.after a long time I am writing comments BECAUSE I am here for appreciate the work not here for down someone.
Craiger1987 keep it up.....
0 -
sriman dutta i got some while searching piyush goel on google i think he has lot work done in mirror image writing/mathematics/making caricatures etc.........
0 -
if you have new post mere bhai....(unity & imatfall). give new to the world...........
friends who do not put right name i think they are fake you both of that type person you know....
likhne aur sochne mein bahut difference hain........
-1 -
sriman bhai pata laga who is piyush goel
-1 -
ok let see
-1

Square Through Squares
in Mathematics
Posted
hello my advice also for you do not write grow up and learn algebra first you understand o.k and we use dear for as a respect not for affection .very well said i am insulting what you and others doing you are not aware of it wonder full .