AbstractDreamer

On 11/16/2023 at 3:41 PM, Markus Hanke said:

Because it is based on the FLRW solution to the EFE, and therein only the spatial part of the metric is non-trivial and carries an expansion factor, there is no time dilation in this cosmological spacetime. 

Both GR in general and its particular solution for this case, the FLRW metric, predate Hubble’s observational findings. Metric expansion is a direct consequence of the laws of gravity, for any homogenous and isotropic distribution of energy-momentum that meets certain criteria; it’s not an independent, stand-alone idea.

Accepted as the basis for a model in the context of cosmology, yes, but not invented or theorised - see above. 

Redshift was historically the first observational evidence that became available to us, but nowadays the Lambda-CDM model covers many other observations too, which were made after Hubble, eg the CMBR with its polarisation, the Ly-wavelength g-wave background, large-scale structure, acoustic baryonic oscillations, ratios of light/heavy elements etc. Among all proposed cosmological models, it is the one that fits the body of all available data the best - though it almost certainly won’t be the last word, I dare predict, because it also does have its problems.

You are welcome to try and find a solution (that isn’t just a trivial diffeomorphism) to the EFE that leads to such a law. Remember that it should also be compatible with all other observations, in order to be a useful cosmological model.

 

But why does the FLRW solution assume that "only the spatial part of the metric is non-trivial and carries an expansion factor, there is no time dilation in this cosmological spacetime." 

On what basis and evidence independent of this assumption do we have that this disposition is true.  Why is it only the spatial metric and not the temporal metric that expands in the case of cosmological scale?

The FLRW solution contains within it the Hubble constant.  The constant describes adiabatic space expansion.  We cant then use the FLRW solution to justify that space expansion exists, because it is a solution that requires it to exist!   Newton's law of gravitation solution does not prove that gravity is force.  It is a solution that requires a force he called gravity.

"The Friedmann–Lemaître–Robertson–Walker metric (FLRW; /ˈfriːdmən ləˈmɛtrə ... /) is a metric based on the exact solution of the Einstein field equations of general relativity. The metric describes a homogeneous, isotropic, expanding (or otherwise, contracting) universe that is path-connected, but not necessarily simply connected" from Wiki

It is describing an expanding universe.  In other words, as it's premises it pre-assumes that the universe is homogenous, isotropic and expanding.  I'm not denying that any observations that subsequently fit the model certainly support the assumptions.  And I'm in no way suggesting there is no space expansion at all. But what about observations that don't fit the model such as data from the JWST?

The lamba-CDM model also uses the Hubble constant presumably derived from the FLRW metric.  Again, it premises that space expands.  A derivation cannot prove a premise.  A geocentric theory does not prove the sun circles around the earth, because it already assumes it does.   We can also add arbitrary complex formulas to make the geocentrism fit new conflicting data such as retrograde precession, just as we can add new mechanisms such as dark energy to make an expanding universe fit redshift and other observations.

CMBR polarisation suggests some space expansion occurred.  And we can arbitrarily parametise a formula to fit exactly what we observe and fit how we understand things work.  But making everything fit comes with the danger of confirmation bias, especially when the fit is arbitrary.   If there are any other mechanisms that we don't understand or haven't yet identified, then making things fit will with certainty blind us to those mechanisms.

Gravitation waves being stretched also fits an assumption of space expansion in the same way as redshifted EM spectra, but the same argument stands.  Why can some unknown from of time dilation not also contribute to gravitation wave stretching -  why must all stretching of gravitational waves be solely caused by space expansion, other than it nicely fits the FLRW metric which is already orientated to only the spatial metric expanding.

Large-scale structure patterns tell us of space expansion vs gravity vs time.  Most theories support the idea of a "force" (dark energy) that counteracts gravity to give us the patterns we see today.  Again we can arbitrarily parametise a formula to fit what we observe with how we understand things, which in this case is:  something (dark energy) is working against gravity, and it does so at different rates depending on when (time).   But why is all dark energy due to space expansion?  Just because we have a solution that takes the position of "only the spatial part of the metric carries an expansion factor"?  So if we are using large-scale structure as evidence for only space expansion, that is a fallacy of circular logic: "Given a solution where only the space metric expands (FLRW), then...  ...only space expands"  Well of course!  It's already given!

I have no response regarding acoustic baryonic oscillations and BB nucleosynthesis right now as I have no understanding at all on those topics.  But evidence for gravity as a force does not refute gravity as spacetime curvature.  In the same way, observations that fit space expansion does not specifically refute other mechanisms.  On the other hand there is quite a lot of refuting evidence against Lamda CDM especially since JWST.

Again, we go back to Hubble's law and cosmological redshift, as the only empirical data source that is not derived from the FLRW premise that only the spatial metric expands, or derived from a parametisation of that metric

Why is there a 1:1 causal link between redshift and space expansion and 1:0 (zero) causal link with redshift and time dilation, when we know it is a single spacetime manifold?  What empirical evidence did Hubble and Lemaitre have in 1920 to believe only space expansion and not time dilation causes redshift.  Why does the FLWR metric choose that only the spatial metric and not the temporal metric expands?

9 hours ago, Endy0816 said:

Biggest for me, is that you would expect to also see some blueshifting, if it had some other cause.

It's also tied to distance. The further something is, the greater the recession velocity. Not what you might expect from a random sample.

Why would we expect to see blueshifting?  We theorised space expansion from the discovery of cosmological redshift.  Not the other way around.  If cosmological redshift had some other cause, it wouldn't change what we measure at all.  It would change our theory.
 

9 hours ago, Markus Hanke said:

Because it is directly correlated to the distance of the source object in question, and that relationship is the exact same no matter in which direction we look, and no matter what else is/is not between here and there. Also, objects don’t just recede from us, but also from each other. 

One must also remember that redshift is only one of several consequences of metric expansion; it’s by no means the only data point.

According the Hubble-Lemaitre law, yes it is correlated to distance.  But why does the Hubble-Lemaitre law attribute 100% of observable cosmological redshift to space expansion, and 0% attributed to cosmological time dilation?  Where is the evidence that cosmological time dilation does not exist?

Before cosmological redshift, there was no such thing as either space expansion or cosmological time dilation. 
After we discovered cosmological redshift, space expansion was accepted/invented/theorised, but why not "cosmological time dilation"?

As far as I have read, redshift IS the only source data point.  Space expansion was theorised from discovering the redshift.   All other data points derive from the theory.  We can't use a derivation to prove a premise.

Hubbles law: v = H₀D

Why can't it be

v = H₀D-P_DT

Where T is the proper time difference and P_D is a constant of proportionality of T which can change over relative proper distance.

In the Hubble=Lemaitre law, T simply has the value of zero.  So yes the further away something is, the faster it is receding, necessarily reaching superluminal velocities above certain distances.

If T has  a non zero then it could be that the further away something is, the faster or slower time is ticking where they are relative to the observer, instead of receding faster, potentially never breaking the limit of c, but not necessarily so.

On 9/8/2023 at 7:22 AM, Markus Hanke said:

Another way to look at this is that in curved spacetimes (of which FLRW is a specific example), energy-momentum is not - in general - a globally conserved quantity, even though it remains conserved everywhere locally. Thus it is not surprising that light does not retain its original frequency when traversing large regions of non-flat spacetime.

I personally think this is a better way to view this, since, after all, these galaxies remain in free fall and do not undergo proper acceleration at any time, despite the velocity-distance correlation.

My point is not about refuting kinematic interpretation of redshift.   A phenomenon of space expanding would certainly cause the cosmological redshift observations that we measure.   This does not mean cosmological redshift observations are entirely and completely explained by space expansion.

If we measure a redshift of 3, why must the entirety of that redshift be caused by space expansion and nothing else?   What evidence do we have that nothing else causes cosmological redshift?

 

On 8/29/2023 at 4:38 PM, Markus Hanke said:

Can you make precise what exactly you mean by “volume” here? Is it a 3-volume of space, as in a geodesic ball for example? Or a 4-volume of spacetime? 

 

I'm not entirely certain what I mean by volume. 

I have two thoughts.   

Firstly, it is the "space expansion", whatever "space" or "volume" it is that is expanding.   So I'm guessing the kinematic interpretation of redshift suggests only a 3volumes expansion, and the (at least partly) gravitational interpretation suggests a 4-volume expansion.   But the accepted interpretation is kinematic only - a 3volume expansion?

Secondly it is about temperature.  Mordred mentioned "increasing volume":

On 5/24/2023 at 7:15 PM, Mordred said:

 It may help to consider that the other major evidence of expansion isn't simply redshift. The most important evidence is the temperature decrease due to an increasing volume.

 I don't know what he means by volume here.  I guess its 3-volume space.  

42 minutes ago, Genady said:

But the ruler is not a wavelength of a travelling photon. The ruler is defined locally. For example, like this:

(Metre - Wikipedia)

Such rulers do not expand.

 

PS. I've picked that half a line because I saw it a pivot for the rest. It is relevant.

So rulers do not expand.  Great.  So what?

14 minutes ago, Genady said:

The ruler does not expand. The expansion is present on the distances of hundreds Mpc's.

-1  for irrelevance.  You quoted half a line and took it out of context to troll a response that has no context to my original text, with no intent other than to derail my topic with graffiti.   

I mean if you read my post you'd realise the expansion is present in the wavelength of a photon.   And if the photon wavelength is the ruler, and the wavelength has expanded, then the ruler has expanded.

Exactly you're wrong and just trolling.  

Define "closer"

34 minutes ago, Genady said:

You can say whatever you want about your pictures. But it is not how GR works. In GR, distances are determined via metric.

Take two events in Minkowski spacetime, for example, events A and B:

Which one is closer to 0?

 

Neither.  As neither axes have any values other than zero.   In this manifold, zero is the only value that can be taken.  Everything has the value zero.

How exactly does the expansion of space result in the lengthening of the wavelength of a photon?  So you have a tiny photon in superposition with regards to its position and momentum travelling through spacetime for 13 billion years.  An excitation propagating through the EM quantum field.  Presumably the field is stretched by expansion, but the photon at any moment is a point.  So how do the properties of the photon get stretched when it is just a point in the field?  Unless the photon isnt a point, and is a line? And if it is a line, then space expansion doesnt occur at any instant but rather over a period?

If a volume experiences space expansion, how do you measure the increase in volume from inside the volume?  I'm guessing you cant because any ruler you have will expand with the volume.  I'm guessing from inside the volume, there is no measurable increase in volume.

If a volume experiences space expansion, how do you measure the increase in volume from outside the volume?  Assuming, for any observer outside the volume, in order to be able to measure a redshifted photon that exceeds the speed of light you have to be sufficiently far away in spacetime such that the observer and the volume do not share a valid local reference frame.  If there is no valid local frame of reference, how do we measure its volume?

If there is no increase in volume locally, and you cannot measure the volume from outside, how does space expansion increase volume and result in lower average energy density?

On 8/27/2023 at 5:39 PM, Genady said:

Yes, I do. So, the rest of the conclusions are wrong. Coordinates don't say anything about the length, area, and volume. Coordinates are arbitrary.

Expansion of space is a solution of the field equation in these conditions.

You're very wrong.  Coordinates are sufficient for comparison.   2<3.   Two is less than Three.  You don't need any units of meters, seconds, degrees or apples, square roots or coloured pixels.

On 8/27/2023 at 8:01 PM, Genady said:

Wanted to add a couple of examples to my previous comment and to demonstrate why this ^^^ is incorrect.

One example is metric that measures number of colored pixels. In this metric, the second shape is larger than the first.

Another metric is square of difference between the pixels in vertical and in horizontal directions. In this metric, the first shape is larger than the second.

Wrong again.  The number of coloured pixels are the same in both, even if you use a metric of number of coloured pixels.  Count them.  There are 4 pixels in both.

 The difference between the pixels in both vertical and horiztonal direction are also the same.  There are two pixels in the vertical direction for both, and 2 pixels in the horizontal directions for both.

Your mistake is assuming the grid lines have significance.  They dont.  Only the numbers on the axes have meaning.

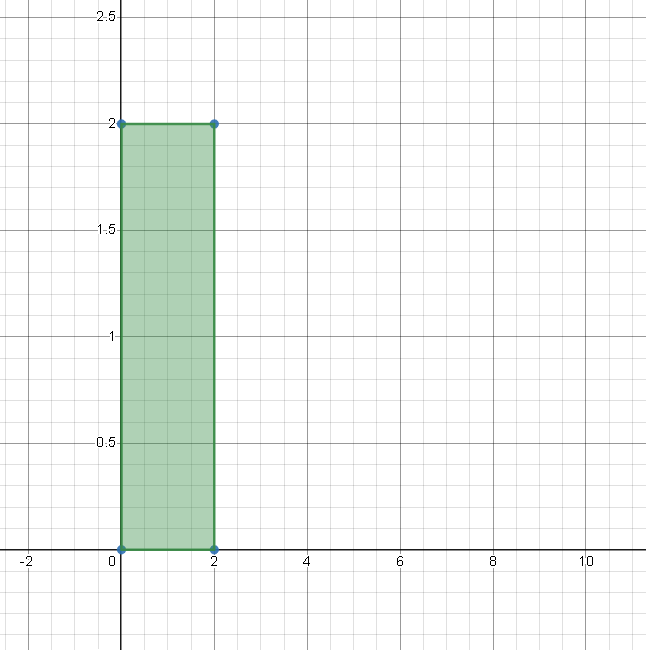
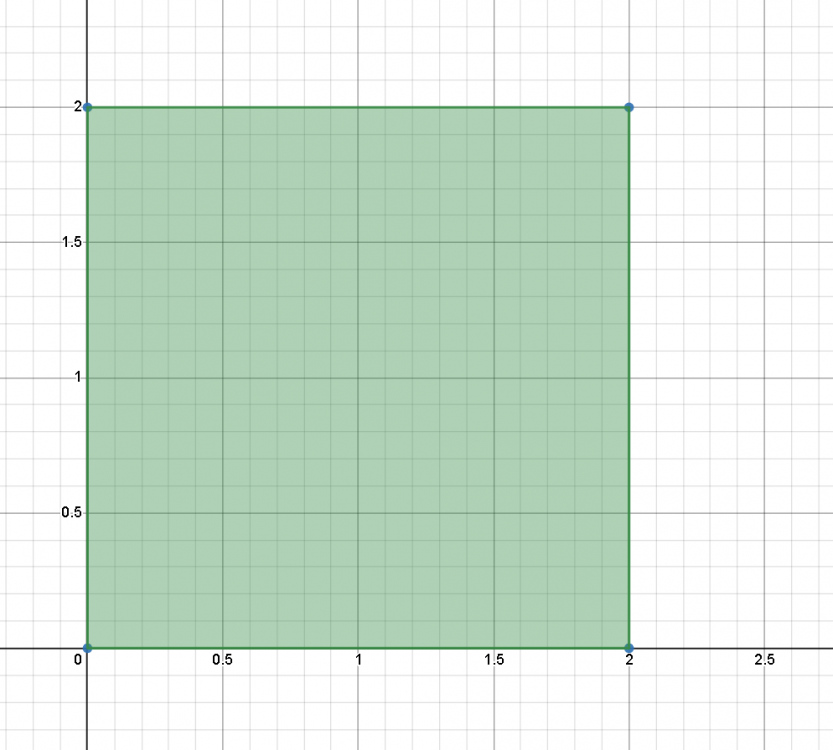
4 hours ago, Genady said:

If the axes in the images above (see https://www.scienceforums.net/topic/131720-cosmological-redshift-and-metric-expansion/?do=findComment&comment=1248849) were labeled with metric units, e.g., 1 km, 2 km, etc., then they could represent a metric. In that case, it would be immediately obvious that they are just two different pictures of the same thing, i.e., a 2 km by 2 km area.

But without units, they can mean anything, for example degrees of latitude and longitude. In this case, they show two shapes, both taking up 2 degrees of latitude and 2 degrees of longitude. Which is larger? This is impossible to tell as it depends where on Earth are they. Moreover, if they are on different planets, it also depends on the planets' radii.

 

Labelling with units is irrelevant.  Which number is bigger?  The number 2 or the number 3?  

On 8/25/2023 at 8:00 PM, Genady said:

To answer questions about length / area / volume one needs metric. Coordinates do not have the required information.

I'm asking which has bigger volume, not how big their volumes are according to some metric.  You don't need a metric to compare volumes, if the coordinate systems are the same, which they are.

The point is stretching axes doesn't change magnitude whatever metric you are using, and so space expansion doesn't change volume.   Both objects are 2x2 square units, and internally consistent with that shape and magnitude - no matter how much an observer stretches the axes, inside the polygon you will never notice any difference.

If you are arguing that space expansion increases volume, then you are saying the square has larger volume than the rectangle, because I changed the magnification and zoomed in significantly on the x-axis.   So then your position is that the volume of each green polygon is a property of the observer and not the polygon.

 

On 8/26/2023 at 2:02 AM, Genady said:

No, not everything is expanding. Only the space on scales of 100 Mpc and up is expanding. The redshift is caused by expanding of the light wavelength together with the expanding space on these scales.

Space does not have to expand at all.  That's the whole point of that paper.  Cosmological redshift does not have to interpreted as due kinematic Doppler shift. 

38 minutes ago, Bufofrog said:

That would be a neat trick.

Here's a neat trick.  Which green polygon has greater volume?
 

On 5/24/2023 at 10:59 PM, Mordred said:

Found the paper I was looking for. Bunn and Hogg examines cosmological redshift in context of both gravitational redshift (would thus include time dilation) and Doppler shift. (Only involves time dilation in the relativistic scenario).

He concludes that as free fall observers and emitters apply, then the latter case is more accurate than the previous.

https://arxiv.org/abs/0808.1081

One of the problems with the former and latter case is that you end up applying a large number of  infinitesimal calculations between observer and emitter.

Wonderful answer thank you!  I feel somewhat vindicated with posting this thread.  This paper seems to answer my questions, at least to my level of comprehension.

I disagree that they conclude Doppler redshift is more accurate than gravitation redshift.  My understanding is that they conclude Doppler redshift interpretation is more natural.  And by natural I assume they mean because its more simplistic to describe.

"Within this frame, you would, by the equivalence principle, interpret their results as a Doppler shift. In so doing, you would be choosing to regard the Doppler family as the natural one, because this family is the one whose behavior is simplest to describe in your chosen frame" page 8 line 4 from the paper above.

At this point, I have an issue with the free fall requirements of the Doppler shift model. That is, no gravitational difference between an observer and its neighbour  along the path of the radiation, where any difference in observed frequency can be attributed as kinematic .   Would a passing gravitational wave not break this local inertial frame between a pair of neighbours?  Over 13 billions years, its hard to imagine how a photon avoids an encounter with a gravitational wave.

On the other hand, a family of observers where each member is at rest relative to its neighbour seems more "natural" to me.  That is, any difference in observed frequency of the photon can be attributed to gravitational redshift - a time dilation cause of redshift.

More important than this choice of frame, is their conclusion that BOTH interpretations are valid.
"There is no “fact of the matter” about the interpretation of the cosmological redshift: what one concludes depends on one’s coordinate system or method of calculation."  page 8 line 17 
"The common belief that the cosmological redshift can only be explained in terms of the stretching of space is based on conflating the properties of a specific coordinate system with properties of space itself. This confusion is precisely the opposite of the correct frame of mind in which to understand relativity." bit further down

This validates my point entirely.  The interpretation of cosmological redshift as Dopplershift or gravitational shift is a matter of choice, and not of facts.  A choice of your arbitrary orientation of your coordinate system, something which I said even before I knew what I was talking about (or rather less that what I know now which is just marginally above zero).

Space expansion is an ARTIFACT of the coordinate system where we CHOOSE zero gravitational causes to cosmological redshift.   

In other words if you choose to zerolise time dilation causes to cosmological redshift, then space expansion neatly explains superluminal recession speeds.

So to address other points of evidence of space expansion as fact rather than choice:

On 5/24/2023 at 7:15 PM, Mordred said:

 It may help to consider that the other major evidence of expansion isn't simply redshift. The most important evidence is the temperature decrease due to an increasing volume.

But I thought space expansion doesn't increase volume.  Unless you are observing the volume from outside using a measurement reference that is independent of such expansion.   If a cube 1m³ expands under space expansion, it's still 1m³ because your ruler also expands with the cube. So wouldn't you have to be outside of the universe to claim any part of it increased in volume?  Or if you are inside the universe measuring another part of it, how do you know your ruler is not being stretched in order to conclude the volume being observed is increasing?

Temperature is measurement of average energy in body/volume right?  "Average" meaning over time.  Even if space expansion "creates volume", how can we say the temperature decreases due to an increasing volume.  Why can we not say "temperature decreases due to a slowing of time" (we are receiving less observables that measure temperature due to time slowing down)?   If I measure 10 photons with a fixed energy propagating from a 1m³ volume over 1 second and we agree to calibrate this reading and call it 10 Hotness.   If I then tell you I have two more experiments, one where I space expanded the volume to 2m³ the volume and another where I time diluted the volume to half the rate of time.   In the space expansion experiment there are now less photons per volume.  In the time dilated experiment there are now less photons per time.   Both experiments would measure a decrease in temperature to 5 Hotness.  But why would we assert that the decrease in temperature is due to only the volume changing?
 

On 5/24/2023 at 7:15 PM, Mordred said:

The other detail to consider is extreme efforts have been made from all the steady state supporters that didn't Like the idea of the BB. Nearly every possible effort to find counter arguments have been tried. They all failed. 

Time dilation aspects included.

 

I don't see why time dilation necessarily contradicts BB or steady state.  Both of which are conclusions from many other factors besides time dilation.  I think its more important to build from the ground up and end up wherever we end up, rather than top down where we want either the BB or a steady state to be a reality and then railroad observations, interpretations and models to fit.  Einstein did that when declaring "God does not play dice", and trying to make QM fit his deterministic belief of the universe.

Ultimately, there is no evidence that excludes time dilation as a factor in cosmological redshift, either through gravitational time dilation or some other kind of mechanics that result in time dilation.   And I don't know why we commonly accept cosmological redshift is fully attributed to kinematic Dopplershift.

41 minutes ago, joigus said:

GR is invariant under re-scalings of time in particular. So a simple re-scaling of time would give you your desired metric. There is no physical information in this distinction. A universe for which the time re-scales as it passes is totally physically equivalent to one in which it's space that expands by means of a time-dependent expansion factor.

First post that addresses my questions.   +1
So time rescaling as it passes is equivalent to space expansion due to a scale factor at that time.  But what determines how much of that change is attributed to which case?

In other words, how much of a redshift measurement is due to space expansion and how much is due to time dilation?  According to the FLRW metric, it is ALL due to space expansion and there is a zero, or at least a net-zero, time dilation effect.   Take in the extreme case where there is no space expansion at all, and all the redshift is caused by time dilation, and the recessional velocity is caused by a  dilation in time rather than by an expansion of space  Why is this such an absurdity?

17 minutes ago, Genady said:

Depending on conditions, different dimensions behave differently. For example, in the spherically symmetric case with central mass, the temporal and the radial dimensions vary while the two spherical dimensions do not. Similarly, in the homogeneous and isotropic case, the spatial dimensions vary while the temporal does not. 

Right, but that is just an artifact of orientation of your coordinate system.  A neat trick to simplify a model.  If you orientate the model to where certain dimensions on a manifold do not vary and other dimension do vary, that does not mean that the dimension that does not vary cannot vary in other models.

So we orientate our redshift observations to one where the temporal dimension does not vary.  That does not mean it cannot vary.

The FLRW metric is orientated towards no allowance for time dilution in flat spacetime - of course it is not going to vary, its orientated that way!  That does not mean there is no time dilution in flat spacetime.

So we go back to my original questions.  Where are the other interpretations / orientations - ones where time dilution can occur in flat spacetime?  Why have we all towed the line fro 100 years with the one accepted orientation where there is no time dilation in flat spacetime?

But more importantly... what are the limitations and consequences of such an orientation?  What might we be missing because of this orientation?

3 minutes ago, exchemist said:

But if wavelength alters and frequency does not, then surely the speed must change. Do you want to develop a model in which c has changed over time, or something?

I'm just a chemist, not a GR specialist. I've never worked with tensors.  @Mordred seems to be one, however. If you are bothered that space and time are treated differently from the viewpoint of expansion you will have to listen to him.  

 

I have no model to develop.  I'm only asking questions that we've had for over 100 years since establishing the accepted model.   

There's a giant elephant in the room saying "Spacetime is a single manifold".

There's another giant elephant in the room saying "Space is different from time because we have conditions in flat spacetime where only space expands and time does not dilute".

There is a clear contradiction here.

But why do we allow space to expand and not allow time to dilute in flat spacetime?

10 minutes ago, Mordred said:

You don't have time dilation due to the homogeneous and isotropic mass distribution. At time of the emitter the universe mass distribution is uniform. At time of observer the same applies. During any point in time between the two the same applies. In essence you don't have time dilation when spacetime is flat at any point in travel time of the null geodesic worldline.

 

But if there was a cosmological, non-relative motion sourced, time dilation effect, could the universal still be homogenous and isotropic wrt mass distribution?  

Ignoring a number of observations that could be argued as violations to homogeneity and also ignoring the violations of isotropy for now (https://en.wikipedia.org/wiki/Cosmological_principle), why or how does homogeneity and isotropy directly refute time dilation in flat space?

What makes the premise of homogenous and isotropic mass distribution irrefutable and sacrosanct?  Where is the evidence, other than ΛCDM model which is based (not solely) upon the FLRW metric and inherits the same premises?  We cannot use models and equations to prove their premises, despite the models and equations matching many observations and predictions.

The implications of the premise that space can expand but time does not dilate when spacetime is flat (not the premise of homogeneity) are enormous.  And the only evidence we have is redshifted measurements of wavelengths that have been travelling cosmological distances and times.  Why has so little scientific attention been paid towards a critical point in our progression of knowledge since 1922, such that there are NO viable alternative interpretations of what is a conflated and ambiguous observation.

We have the Many Worlds and Copenhagen interpretations of observations in quantum phenomena.  But we only have the space expanding interpretation of cosmological redshift and absolutely forbid any time dilation in flat space, when GR is screaming spacetime is continuum?  Just seems like an enormous elephant in the room to me.

19 hours ago, exchemist said:

Just on this small point, the relationship between speed, c, frequency, ν, and wavelength, λ, is c = νλ. This is true of any wave (light, sound, water etc). So, given that for light c is constant, as observed by us (that being the basic premise from which relativity starts), once you have said its wavelength increases there is no need to say frequency decreases: the relationship is automatic. Everyone knows this, so that's why you don't see it mentioned. 

Yes the relationship between frequency and wavelength automatic.  But wavelength is a measure of space, which we allow to expand as described by the FLRW metric, and frequency is a measure of time... which apparently cant expand (specifically in the case of cosmological redshift and not in the case of dilation).  Why?  Spacetime is a continuum.  Why, in the case of interpreting cosmological redshift, is it not a continuum?

19 hours ago, exchemist said:

I'm not sure anyone would claim that it is the only interpretation. In science one never formally closes the door to other hypotheses. Surely the claim of science is that it is the leading interpretation, to the extent that there are currently no serious alternatives? 

So the reason @Genady is asking you to put forward an alternative is that there are no viable alternatives that anyone knows about, at least not at the moment.  

 

If there are no viable alternatives, then it is the only viable interpretation.  Which is rather surprising considering there is no evidence for space expansion other than cosmological redshift observations.   We observe cosmological wavelengths redshifted in 1912, we theorise space can expand, we develop a model (FLRW) to match redshift observations based on that in 1922.  We can use the model to match subsequent observations based on the same assumptions.  But we cannot then go and claim the model and the mathematics proves space expands.

In analogy:  Newton observed an apple fall, he theorised gravity as a force, he developed models and maths to match his "falling" observations.  We can use the model to match subsequent observations and make predictions rather accurately in most circumstances.  But you cannot use Netwon's law to claim gravity is a force.

10 hours ago, Mordred said:

You will note no time dilation is involved.

Why is that?  Why must there be no time dilation?  What is it about cosmological redshift observations that says space expands but time does not dilute?  If relative motion can dilate time, why should non-relative motion not?  Why are we applying "classical reasoning" to cosmological redshift observations?

1 minute ago, Genady said:

I am not justifying it. I am answering your question, "it is called space expansion and not spacetime expansion.  Why?"

As I've said above, if you wish to suggest a different interpretation, go ahead.

I'm not even really asking to justify the FLRW metric.  It is perfectly justified - given its assumptions and premised.

I'm asking to justify why space expansion is the only interpretation of cosmological redshift.

You've said for me to suggest a different interpretation and then explicitly repeated it.  Stop derailing my thread please.

That's the FLRW metric.  One of it's premises is that space is expanding.  After that assumption it then describes the expansion.  But ill say it again, we can tear apart the FLRW equations all day, you can never use it to justify its own premise.  So please, stop using the FLRW to justify that space is expanding.  The FLRW describes how it expands.  It does NOT justify it.

We have to go back to observational evidence - cosmological redshift.   

It is very logical why cosmological redshift is interpreted as space expansion - it makes a lot of sense. 

But spacetime is not commonly sensible. And having a sensible interpretation does not mean that there are no alternatives. 

2 minutes ago, Genady said:

If you want to suggest a different metric for the homogeneous and isotropic universe, go ahead.

If you want to suggest a better model of the universe, go ahead.

Anyway, there is only one metric, the spacetime metric. In the FLRW metric, the space rather than the metric of space is expanding. 

I'm not suggesting anything.  I'm asking questions.  All of the answers so far have missed the real crux of my questions.

"There is only one metric, the spacetime metric" and yet it is called space expansion and not spacetime expansion.  Why?

1 minute ago, Genady said:

In the second part of the first sentence that you've quoted in the OP. It applies to any redshift, the cosmological one included.

Right.  So.... why is the metric of space expanding and the metric of time NOT changing, in the specific case of the widely accepted interpretation of cosmological redshift.

2 minutes ago, Mordred said:

As mentioned GR is used, the FLRW metric is simply an accurate simplified derivative of GR.

It is used in the FLRW metric, AFTER the interpretation of space expansion.  Space expansion is a premise of the FLRW metric  You cant use a metric to justify its premises.  Once we assume cosmological redshift is the observation resulting from space expansion, the FLRW metric ensues.  Before that, it is meaningless to talk about the FLRW.

I'm not asking about the GR used within FLRW, I'm asking about its premise that space is expanding.
Show me where GR is used in the interpretation of cosmological redshift as something other than space expansion.

9 minutes ago, Mordred said:

I can post the equations after work but the FLRW metric derives from the Newton approximation dust solution in commoving coordinates.

If the equations assume space expansion exists in order to describe it, then they wont help question space expansion only reinforce and it.

Where is the evidence for space expansion other than cosmological redshift?

What are alternative interpretations of cosmological redshift other than space expansion? 

7 minutes ago, Genady said:

We use GR.

Show me where.

10 minutes ago, Genady said:

It is both.

It is, but show me where cosmological redshift is interpreted as a decrease in frequency then.

12 minutes ago, Genady said:

This how the metric of homogeneous and isotropic universe works. See FLRW metric.

This is how the FLRW fits observations of cosmological redshift and interpretation of it as space expansion.  You can't use a parametisation to prove it's assumptions.